Модели развития операций по схеме сложных процентов

В финансово-коммерческих операциях используется схема сложных процентов, если начисляемый процент (Г) (доход от капитала) суммируется с исходным капиталом (Р) и на следующем интервале начисления процент начисляется уже от всей образовавшейся суммы (Р + /). Этот вариант иногда называют капитализацией, или реинвестированием, или проценты на проценты. В этом случае сумма накопленного капитала составит:

• к концу первого года.

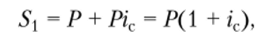
где i_c — относительная величина годовой ставки сложных ссудных процентов;

• к концу второго года.

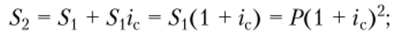
• к концу третьего года.

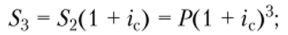
• к концу /7-го года.

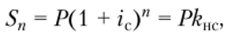
где k_HC — коэффициент наращения; k_llc = (1 + Q".

Таким образом, накопление капитала по схеме сложных процентов образует возрастающую числовую последовательность S₀, S1, S₂y S_3f…, S_n, которая представляет собой геометрическую прогрессию с первым членом ⁼ S$ = Р и знаменателем q = 1 + ic. В соответствии с этим можно записать формулу для определения любого ее члена: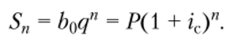

Таким образом, получена модель наращения по формуле сложных процентов:

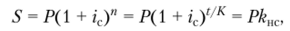
где t — срок контракта в днях; к_т — коэффициент наращения.

Выводим формулы для определения таких показателей финансовой операции, как:

• величина первоначальной суммы.

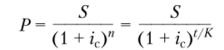
• (математическое дисконтирование при начислении сложных процентов);
• • относительная величина процентной ставки

• (одна из наиболее применяемых формул, используется для оценки доходности финансовой операции);
• • срок ссуды (лет)

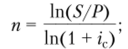
• срок ссуды в днях.

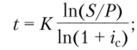
• продолжительность года в днях.

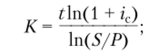
• коэффициент наращения.

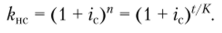
Если на протяжении всего срока контракта процентная ставка изменяется, то получим другую математическую модель определения наращенной суммы.

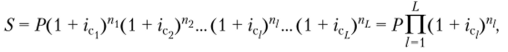
где п — 1-й интервал начисления процентов, /= 1, L; L— ко;

L

личество интервалов начисления; к_ис = П (1 + К)" ¹ — коэффи;

i=i

циеит наращения.

Начисление сложных процентов может осуществляться несколько раз в году: по месяцам, кварталам, полугодиям. В таких случаях указывается ставка на периоде, а наращенная сумма находится по формуле.

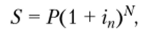
где i_n — ставка на периоде начисления; N — количество интервалов начисления в течение срока действия контракта.

В случае когда начисление сложных процентов осуществляется через равные промежутки времени п, указывается номинальная годовая процентная ставка у, пользуются следующей формулой:

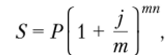
где т — количество интервалов начисления за год; п — срок контракта в годах; N=mn — количество интервалов начисления за весь срок контракта.

На практике применяется еще и непрерывное начисление процентов по номинальной годовой процентной ставке j. В этом случае величину наращенной суммы находят из следующего выражения:

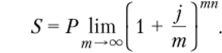
Затем при переходе к пределу при т —? используя известную формулировку второго замечательного предела.

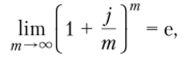
получим такое уравнение:

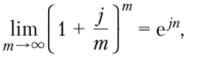
тогда для определения наращенной суммы получим формулу.

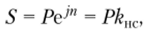
где k_HC = e^jn — коэффициент наращения при непрерывном начислении процентов по номинальной годовой ставке у.

Приведенные модели позволяют проводить вычисления различных показателей финансовых операций.

Пример 6.9. Коммерческие банки С и D начисляют доход один раз в полгода, причем банк С по простой ставке, а банк D по сложной ставке процентов. Через год в этих банках средства инвестора увеличиваются на 60%. В какой банк выгоднее положить деньги на пол года и в какой — на полтора года?

Решение

По условию задачи коэффициенты наращения банков С и D равны, поэтому k_u = k_llc = 1,6, откуда для банка С ставка простых процентов определяется из выражения.

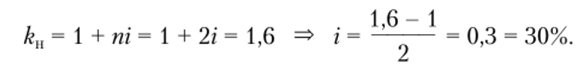
Для банка D ставка сложных процентов составляет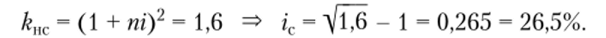

Следовательно, выгоднее положить деньги на пол года в банк С. Для сравнения результатов финансовых операций с банками С и D можно составить следующую таблицу.

Из данных таблицы следует, что на полтора года (как и вообще на любой срок свыше года) выгоднее положить деньги в банк, А поскольку k_HC = 2,02 > k_n = 1,9.

Пример 6.10. М. Е. Салтыков-Щедрин описывает в «Господах Головлевых» такую сцену: «Порфирий Владимирович… сидит у себя в кабинете, исписывая цифирными вкладками листы бумаги. Па этот раз его занимает вопрос: сколько было бы у него теперь денег, если б маменька… подаренные ему при рождении дедушкой… на зубок сто рублей… не присвоила себе, а положила бы вкладом в ломбард на имя малолетнего Порфирия? Выходит, однако, немного: восемьсот рублей…».

Определите сложную ставку процентов годовых ломбарда по вкладам, если Порфирию в момент его расчетов было 50 лет.

Решение

п = 50; Р = 100 руб.; S = 800 руб.

По формуле сложных процентов наращенная сумма равна: 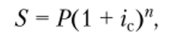откуда ставка сложных процентов составит.

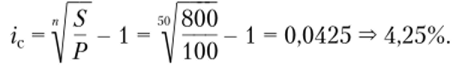
Пример 6.11. Знаменитый американский ученый и государственный деятель Бенджамин Франклин завещал жителям города Бостона 1 тыс. фунтов стерлингов на следующих условиях:

• • деньги давать под 5% годовых молодым ремесленникам;
• • через 100 лет из накопленных денег (с учетом процентов на проценты) 100 тыс. фунтов стерлингов пустить на строительство общественных зданий;
• • оставшиеся после этого деньги отдать под те же проценты еще на 100 лет;
• • по истечении этого срока накопленную сумму разделить между бостонскими жителями и правлением Массачусетской общины, которой передать 3 млн фунтов стерлингов.

Сколько денег должно было достаться бостонским жителям через 200 лет после смерти Б. Франклина (он умер в 1790 г.)?

Решение

Р = 1000 ф. ст.; i_c = 5%; п = 100 лет.

1. Завещанный капитал через 100 лет составил.

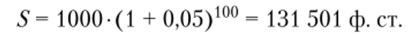
2. После выделения 100 000 ф. ст. на постройку общественных зданий осталось.

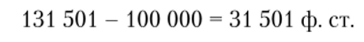
3. Через 100 лет наращенный капитал составил.

4. Бостонским жителям из этой суммы после вычета 3 млн ф. ст. осталось.

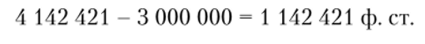
Пример 6.12. Начисление процента на сумму срочного вклада с условием ежемесячной капитализации процентов.

Банк 20.07 заключает с вкладчиком договор срочного вклада на 3 месяца (срок возврата вклада — 20.10). Сумма вклада — 15 тыс. руб. Процентная ставка — 22%. 20-го числа каждого месяца действия договора производится капитализация начисленных процентов. Переоформление вклада по окончании срока действия договора на ранее действовавших условиях срочного вклада договором не предусматривается. Выплата причисленных к сумме вклада процентов осуществляется по истечении срока действия договора.

В течение срока действия договора банк трижды — 20.08, 20.09 и 20.10 производит капитализацию начисленных процентов во вклад. 20.10 — срок окончания договора срочного вклада, вкладчик не явился за вкладом в установленный договором срок. В этот же день после окончания операционного дня банк переоформляет указанный срочный вклад во вклад до востребования.

Вкладчик 28.10 получает сумму вклада до востребования и начисленные за период с 20.10 по 27.10 включительно (8 календарных дней) проценты по установленной ставке 4%.

Полный срок срочного вклада (20.07—20.10) — 93 календарных дня (я), период начисления процентов по ставке срочного вклада — 22% (20.07—19.10) — 92 календарных дня (п — 1).

Полный срок вклада до востребования (20—28.10) — 9 календарных дней (п), период начисления процентов, но ставке вклада до востребования — 4% (20—27.10) — 8 календарных дней.

Порядок начисления банком процентов на сумму вклада:

• сумма срочного вклада на 21.08 (с капитализацией процентов, начисленных за период с 20.07 по 19.08 включительно).

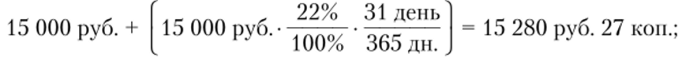
• сумма срочного вклада на 21.09 (с капитализацией процентов, начисленных за период с 20.08 по 19.09 включительно).

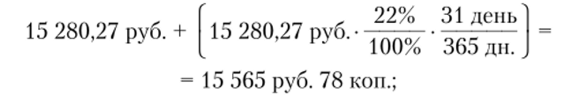
• сумма срочного вклада по состоянию на конец операционного дня 20.10 (с капитализацией процентов, начисленных за период с 20.09 по 19.10 включительно), в конце рабочего дня 20.10 и переоформленного во вклад до востребования.

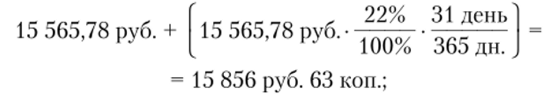
• сумма начисленных на вклад до востребования процентов (за период с 20.10 но 27.10 включительно):

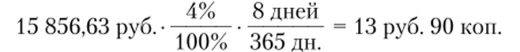
Таким образом, общая сумма возврата денежных средств вкладчику составит на 28.10 15 870 руб. 53 коп., из которых 15 856 руб. 63 коп. — сумма срочного вклада с учетом капитализированных процентов и 13 руб. 90 коп. — проценты, начисленные за время, прошедшее с момента переоформления указанного срочного вклада во вклад до востребования.

Пример 6.13. Начисление процентов на сумму срочного вклада по формуле сложных процентов.

Банк 05.08 заключает с вкладчиком договор срочного банковского вклада на 21 день (срок возврата вклада — 26.08). Сумма вклада — 15 тыс. руб. Процентная ставка — 15%. По условиям договора начисленные, но итогам каждого дня срока действия депозита проценты увеличивают сумму вклада.

Полный срок вклада (05—26.08) — 22 календарных дня (/?), период начисления процентов по вкладу (05—25.08) — 21 календарный день (п — 1).

26.08 банк возвращает вкладчику вклад (с учетом ежедневной капитализации процентов) в сумме:

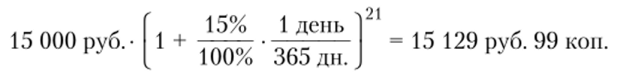
Пример 6.14. Банк выдал коммерческому предприятию 16.08 валютный кредит иод контракт на покупку товаров на сумму 10 000 долл. США, срок кредита — 2 месяца (до 16.10); ставка процентов — 35% годовых за полное количество качендарных дней из расчета 360 дней в году, при подсчете количества дней в периоде граничные дни (первый и последний) считаются за 1 день;

порядок выплаты кредита: 16.09 — проценты за первый месяц;

16.10 — проценты за второй месяц и сумма кредита; штрафные санкции по ставке сложных процентов составляют 0,5% от просроченных сумм кредита за каждый день просрочки. Очередность погашения просроченной задолженности: в первую очередь погашаются начисленные штрафы, затем сумма процентов и сумма кредита.

Фактически 16.09 клиент погасил проценты за первый месяц кредита. Далее кредит погашался в следующей последовательности:

22.10 клиент перевел 2600 долл. США в счет погашения задолженности; 25.10 клиент перевел 3100 долл. США в счет погашения задолженности, а 30.10 клиент заявил, что готов погасить свою задолженность в полном объеме.

Определите величину задолженности клиента на 30.10.

Решение.

Определяем:

• сумму задолженности на 16.10.

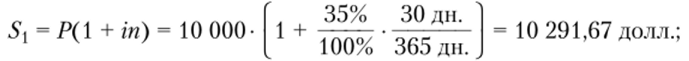
• сумму задолженности на 22.10 до внесения первой суммы на погашение.

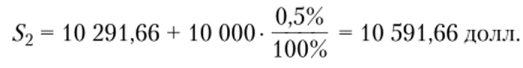
После частичного погашения сумма долга составит.

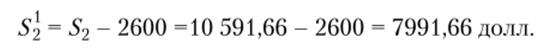
Рассчитаем сумму задолженности 5з на 25.10 до внесения второй суммы на погашение:

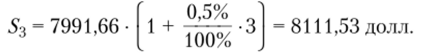
После частичного погашения долга сумма долга составит 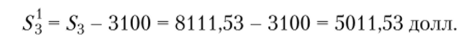Определяем сумму задолженности 5₄ на 30.10.

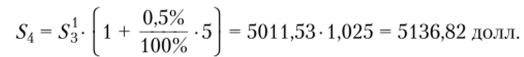
Следовательно, на 30 октября полная задолженность по кредиту, процентам и начисленным штрафам составит 5136,82 долл. США.