Постановка игровых задач

Решения, принимаемые в коммерческой деятельности, направлены, как правило, на удовлетворение определенных потребностей населения и связаны обычно с распределением ресурсов предприятия: товаров, денег, людей и т. д.

Рассмотрим систему управления коммерческим предприятием, структуру которого можно представить как орган управления (дирекция) и некоторое количество производственных единиц (товарных секций или отделов).

Каждый отдел реализует некоторый набор товаров. В зависимости от организации и правового положения руководство может иметь те или иные возможности управления работой отделов. Предполагается, что в данном случае наиболее действенной формой управления является оптимальное распределение ресурсов.

Отдел самостоятельно может выбрать программу выполнения товарооборота. Целью коммерческого предприятия является максимизация доходов или минимизация затрат, связанных с продажей товаров.

Сведем данную задачу к игровой модели. Обозначим через п число отделов; т — число различных товарных ресурсов; X, — вариант выполнения товарооборота, принимаемый г-м отделом, г = 1, и; у₂ — вид товарного ресурса, выделяемый коммерческим директором, у = 1, т ау — набор товаров, реализуемый г-м отделом при выделенииу'-го вида товарного ресурса, i=l, п,у = 1, т Y — суммарный объем ресурсов, которыми распоряжается коммерческий директор; С — доход или потери, связанные с реализацией товара.

В терминах игровой модели можно дать следующую интерпретацию введенных обозначений: п — число стратегий отдела; т — число состояний среды; х, — — /-я стратегия, i = 1 , п; у, — у'-е состояние среды, у = 1, т; а_у — исход, получаемый при стратегии х, и состоянии среды yj, i = 1, и, у = 1, т.

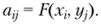
Математическая модель сформулированной задачи имеет следующий вид; максимизировать (минимизировать) величину.

при ограничениях.

Продажа товаров коммерческим предприятием может быть описана соотношением.

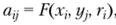
где г, — фактор, значение которого хорошо известно руководству г-го товарного отдела, но руководство коммерческого предприятия достаточной информации о нем не имеет.

Это могут быть отбраковка товаров, колебания спроса, неравномерность потока покупателей и т. д. Таким образом, выделенный ресурс у, и выбранная технология работы товарного отдела х, не дают руководству коммерческого предприятия полной информации о том, какая будет реализована продукция Ujj — это знает только г-й отдел. Очевидно, что сушествует зависимость х, = у (уу, г,-), в которой есть неопределенные факторы г, € А/, конкретные значения которых в момент распределения ресурсов у_г между товарными отделами неизвестны руководству коммерческого предприятия. В этих случаях разумно воспользоваться принципом гарантированного результата, т. е. поставить задачу: найти такое распределение ресурса yj_y чтобы при этом достигался.

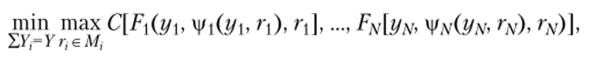
следовательно, руководство магазина так распределяет ресурсы, чтобы минимизировать потери при наихудшем возможном значении неопределенного фактора, или.

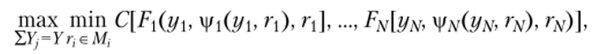
следовательно, руководство коммерческого предприятия так распределяет ресурсы между товарным отделом, чтобы максимизировать доходы при наихудшем возможном значении неопределенного фактора.

Пример 3.1. Рассмотрим постановку и решение следующей задачи. Коммерческое предприятие заключило договор на централизованную поставку овощей из теплиц на сумму 10 000 руб. ежедневно. Если в течение дня овощи не поступают, магазин имеет убытки в размере 20 000 руб. от невыполнения плана товарооборота. Магазин может осуществить самовывоз овощей фермера. Для этого он может сделать заказ в транспортном предприятии, что вызовет дополнительные расходы в размере 500 руб. Однако опыт показывает, что в половине случаев посланные машины возвращаются без овощей. Можно увеличить вероятность получения овощей от фермера до 80%, если предварительно посылать туда своего представителя, что требует дополнительных расходов в размере 400 руб. Существует возможность заказать дневную норму овощей у другого надежного поставщика — плодоовощной базы по повышенной на 50% цене. Однако в этом случае, кроме расходов на транспорт (500 руб.), возможны дополнительные издержки в размере 300 руб., связанные с трудностями реализации товара, если в тот же день поступит и централизованная поставка от фермера. Какой стратегии надлежит придерживаться магазину, если заранее неизвестно, поступит или не поступит централизованная поставка?

Построим игровую модель этой задачи. Игроками являются представители магазина и поставщика.

Перечислим стратегии первого игрока — поставщика.

П — поставка своевременная;

П2 — поставки нет.

У магазина имеются четыре стратегии поведения:

Mi — ожидать поставку, нс принимая дополнительных мер;

М₂ — послать к поставщику свой транспорт;

М3 — послать к поставщику представителя и транспорт;

М4 — заказать поставку у плодоовощной базы.

Всего возможны восемь совместных ситуаций, отражающих затраты магазина (руб.), которые представлены в табл. 3.1.

Таблица 3.1

Для того чтобы легче было разобраться в сложившихся ситуациях и по возможности оценить их, составляют платежную матрицу. Матрица имеет т строк — по числу стратегий первого игрока и п столбцов — по числу стратегий второго игрока. На пересечении i-й строки и j-го столбца ставится платеж второго игрока первому в ситуации, когда применены i-я и j-я стратегии игроков. Если в данной ситуации выигрывает второй игрок, то платеж будет иметь знак «минус». Платежная матрица данной задачи представлена в табл. 3.2.

Таблица 3.2

Выбор стратегии магазина зависит от надежности фермера как поставщика продукции, которую можно оценить величиной вероятности рj. Тогда величина/^ ⁼ 1 ~Р представляет собой величину ненадежности поставщика. По данным табл. 3.2 можно составить уравнения затрат магазина Е от надежности поставщика для каждой стратегии магазина.

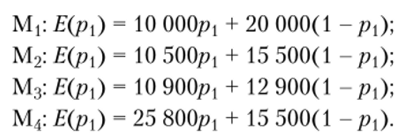
Если своевременная поставка осуществляется с вероятностью 0,4, тогда ожидаемые затраты магазина составят соответственно.

Таким образом, минимальные расходы магазин понесет в том случае, если примет стратегию М₃, т. е. не только пошлет фермеру автотранспорт, но и отправит туда своего представителя.

Пример 3.2. Формирование платежной матрицы рассмотрим на примере задачи о взаиморасчетах.

Известно, что для того чтобы начать какое-либо дело в торговле, по производству продукции или оказанию услуг, необходимы средства, которые могут быть собственными и (или) заемными. Предприятие создается с целью получать прибыль (доход) от своей деятельности, а для этого необходимо вложить (инвестировать) капитал в основные средства (в помещение, оборудование и т. п.), в оборотные средства (в материалы, товары и т. п.), в рабочую силу.

В процессе деятельности предприятия происходит изменение средств и источников этих средств, т. е. происходит движение средств и их источников. При этом на любой момент времени (дату) будет выполняться «закон сохранения»:

Поскольку источники средств подразделяются на два вида — собственные (капитал) и заемные (обязательства), тогда может быть записано уравнение в виде.

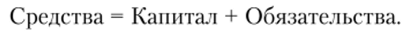
Обязательства могут иметь различную форму: кредиты банков, акции, облигации, векселя, товары, отданные предприятию на реализацию или на консигнацию (товарный кредит). Все эти юридические или физические лица являются кредиторами предприятия и вправе рассчитывать на получение доходов (дивидендов) от совместной деятельности.

Описание деятельности предприятия проводится на языке бухгалтерского учета, понятном всем предпринимателям независимо от области их деятельности: промышленность, строительство, сельское хозяйство, машиностроение, торговля, образование и др.

Бухгалтерский учет позволяет выявить финансовый результат — чистую прибыль предприятия путем подсчета разности доходов и расходов за определенный период.

Предприниматели А, В и С заключили договор для совместного проведения цепочки посреднических операций на май на условиях самостоятельного финансирования своей части. Взаимное переплетение трех вариантов коммерческих операций послужило поводом к образованию взаимозадолженностей, зарегистрированных бухгалтером в хронологическом порядке за май, которые представлены в табл. 3.3.

Таблица 3.3

Всего вариантов взаимозадолженностей при трех участниках шесть: 1) АВ 2) АО, 3) ВА; 4) ВО, 5) СА; 6) СВ. Просуммируем одноименные варианты, например, Е (А, D) = Е_{(А, В) + Е₂(А, В) = 1000 + + 2000 = 3000 у.е. и т. д., а результаты запишем в сводный журнал вза и м пых за до л же н и остей.

Таблица 3.4

Задача заключается в том, чтобы к концу расчетного периода (в данном случае к концу месяца) произвести окончательные расчеты между участниками игры. Это можно сделать двояким образом: а) произвести все шесть расчетов между участниками в соответствии с данными таблицы по принципу «каждый сам за себя»;

б) сделать необходимые расчеты и произвести взаимозачеты долгов. При втором варианте число платежей сократится вдвое, соответственно для расчетов потребуется меньше наличных денег.

При расчетах между клиентами А и В Е (А, В) = 3000 — это сумма долга, которую А должен получить от В, а Е (В, А) = 800 — сумма к получению В от А. Сальдо АДА, В) = ДА, В) — Е (В, А) = 3000 — - 800 = +2200 означает сумму долга, которую А должен получить от В при окончательном расчете.

При расчетах между А и С получим АДА, С) = Е (А, С) — ДС, А) = = 500 — 1500 = -1000, а этот результат означает прямо противоположное — сумму к оплате задолженности господина А перед господином С или, что-то же самое, АД С, А) = -АЕ (А, С) = +1000 представляет собой сумму к получению С долга от А.

И наконец, расчет сальдо АЕ (В, С) = Е (В, С) — ДС, В) = 800 — -700 = +100 является заключительным во взаиморасчетах между тремя участниками коммерческой операции.

При этом варианте расчетов следует провести всего три платежа для погашения взаимных задолженностей, для чего потребуется 2200 + 1000 + 100 = 3300 у.с. — меньшая сумма в сравнении с общей суммой 7300.

В общем случае при числе участников т количество возможных (неповторяющихся) корреспонденций равно т (п — 1), при т = 10 число корреспонденций равно 10(10 — 1) = 90. Для систематизации таких расчетов можно записать данные сводного журнала в виде матрицы выигрышей (табл. 3.5).

Транспонированная матрица Е^Т есть матрица проигрышей (табл. З. б). Если из матрицы выигрышей Е вычесть матрицу Ё, то получим матрицу сальдо окончательных расчетов как разность АЕ = Е — Е^т (табл. 3.7).

Полученная таблица АЕ обладает следующими свойствами:

а) сумма всех ее элементов равна нулю; б) элементы таблицы зеркально симметричны относительно главной диагонали, т.с. всегда АЕ (Х_У У) = -АДУ, X) для любых X, Y= А, В, С.

Таблица 35

Таблица 3.7

Таблица АЕ, т.с. таблица сальдо окончательных задолженностей, и способ се получения, описанный выше, составляют основу компьютерной технологии бухгалтерского учета.

Используя введенные выше обозначения, можно записать основное уравнение взаимных расчетов для любого количества участников в матричной форме.

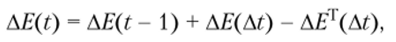
где AE (t), AE (t — 1) — матрицы, в которых со знаком «+» или «-» записаны окончательные сальдо взаимных задолженностей, соответственно на конец t и начало времени t — 1.

Матрица AE (At) — таблица, в которой записаны суммы выигрышей («счета к получению») за рассматриваемый период, а транспонированная матрица АЕ^т(Ас) — это таблица, в которой записаны просуммированные за тот же период суммы проигрышей («счета к оплате») тех же участников игры. Причем все матрицы А?(Г), AE (t — 1), AE (At), AE^T(At) квадратные, определяемые числом участников игры.