Устойчивость цифровых фильтров

Устойчивость нерекурсивных цифровых фильтров. Поскольку аналоговыми прототипами нерекурсивых фильтров служат линейные цепи без ОС, то они относятся к устойчивым динамическим цепям. Нерекурсивный фильтр устойчив еще и потому, что имеет конечную импульсную характеристику.

Устойчивость рекурсивных цифровых фильтров. Рассмотрим вопрос об устойчивости рекурсивных цифровых фильтров, которые являются дискретными аналогами линейных динамических систем с ОС. Если задана совокупность значений у-у₁ _₂,…, у,, то при отключенном входном сигнале цифровой фильтр теоретически будет формировать элементы бесконечной последовательности отсчетов у_р y_i+v y_i+2,…, у_п, которые считают свободными колебаниями.

С точки зрения импульсной характеристики устойчивость цифрового фильтра означает, что его реакция на ограниченное по размерам входное воздействие также ограничена. Чтобы цифровой фильтр был устойчив, необходимо и достаточно выполнения условия.

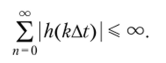
Наиболее распространено другое понятие устойчивости цифрового фильтра. Рекурсивный цифровой фильтр является устойчивым, если возникающий в нем свободный процесс характеризует убывающую или постоянную последовательность элементов, т. е. значения у_п при п —* оо не превышают некоторого положительного числа М независимо от выбора начальных условий.

В рекурсивном фильтре на основании алгоритма (6.34) свободные колебания определяются в результате решения линейного разностного уравнения.

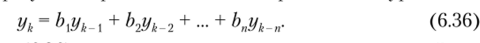
Решение урвнения (6.36) по аналогии с принципом решения линейных дифференциальных уравнений найдем в виде показательной функции

с неизвестным пока значением а. Подставив выражение (6.37) в формулу (6.36) и сократив на общий множитель, убеждаемся в том, что, а является корнем характеристического уравнения

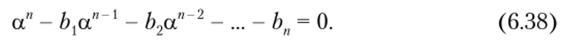
Уравнение (6.38) в точности совпадает с уравнением, которому удовлетворяют полюсы системной функции рекурсивного цифрового фильтра (6.35).

Положим, что корни а, а₂,…, а_/; уравнения (6.38) найдены. Тогда общее решение разностного уравнения (6.36) будет иметь следующий вид:

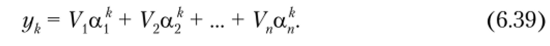
Значения постоянных коэффициентов V_v V₂,…, V_n в формуле (6.39) необходимо выбирать такими, чтобы удовлетворялись начальные условия.

Если все полюсы системной функции (6.35), т. е. модули постоянных вещественных чисел 2, = а_1? z₂ = а₂,z_n = а", не превосходят единицы (по модулю меньше единицы), располагаясь внутри единичного круга с центром в точке 2 = 0, то на основании формулы (6.39) любой свободный процесс в цифровом фильтре будет описываться членами убывающих геометрических прогрессий, и фильтр является устойчивым.

Критерий устойчивости рекурсивных цифровых фильтров. Вопрос об устойчивости рекурсивного фильтра можно решить, связав эту задачу с определением расположения корней многочленов на комплексной плоскости.

Как уже отмечалось, преобразование

взаимно-однозначно отображает левую полуплоскость комплексной переменной v на единичный круг в комплексной 2-плоскости с центром координат в точке 2 = 0. Действительно, точке v = -1 соответствует точка 2 = 0. При этом мнимая ось на^{-плоскости,} т. е. совокупность точек на плоскости с координатами v =jz (г — произвольное вещественное число), отображается в множество точек единичной окружности z = -e^y2arctgs.

Обратимся к характеристическому уравнению цифрового фильтра

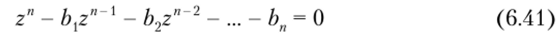
и подставим в него переменную 2, связанную с переменной v согласно формуле (6.40):

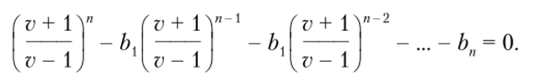
Данный полином может быть приведен к общему знаменателю (v — 1)". В результате получим характеристическое уравнение относительно переменной v:

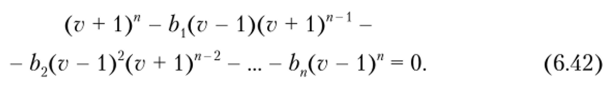
Если левая часть данного многочлена по степеням v имеет корни только в левой полуплоскости, то исходный характеристический многочлен (6.41),.

описывающий цифровой фильтр, имеет корни, располагающиеся лишь в единичном круге на 2-плоскости. В этом случае рекурсивный фильтр является устойчивым.

Цифровые фильтры 1-го и 2-го порядков структурно проще, п их анализ проводится с помощью достаточно несложных операций. Кроме того, цифровые фильтры высоких порядков всегда можно представить в виде соединений цифровых фильтров 1-го и 2-го порядков.

Пример 6.18.

По описанному критерию исследуем устойчивость рекурсивного цифрового фильтра 3-го порядка с характеристическим уравнением.

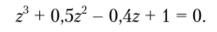
Решение.

Воспользовавшись формулой (6.41), запишем преобразованное характеристическое уравнение:

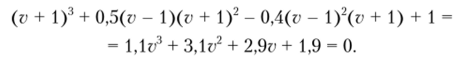
Здесь все коэффициенты положительны и в то же время а,", — а₀а₃ = 6,9 > 0. Данный многочлен отвечает условиям теоремы Гурвица (см. гл. 4). Значит, согласно критерию Рауса — Гурвица анализируемый рекурсивный фильтр устойчив.