Нормальный закон распределения

Нормальный закон распределения называют еще законом Гаусса. Этот закон играет важную роль и наиболее часто используется на практике по сравнению с другими законами распределения.

Основная особенность этого закона состоит в том, что он является предельным законом, к которому приближаются другие законы распределения. В теории надежности его используют для описания постепенных отказов, когда распределение времени безотказной работы вначале имеет низкую плотность, затем максимальную и далее плотность снижается.

Распределение всегда подчиняется нормальному закону, если на изменение случайной величины оказывают влияние многие, примерно равнозначные факторы. Нормальный закон распределения описывается плотностью вероятности.

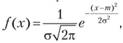
где е = 2,71 828 — основание натурального логарифма;? = 3,14 159; т и? — параметры распределения, определяемые по результатам испытаний.

Колоколообразная кривая плотности распределения приведена на рис. 4.2.

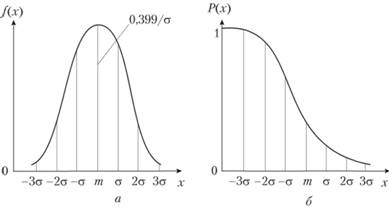
Рис. 4.2. Кривые плотности вероятности (а) и функции надежности (б) для нормального распределения.

Параметр т = Мх представляет собой (в пределе, по теореме Гливенко) среднее значение случайной величины х, оцениваемое по формуле.

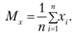
Параметр? — среднее квадратическое отклонение случайной величины х, оцениваемое по формуле.

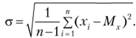
Интегральная функция распределения имеет вид.

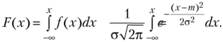
Вероятность отказа Q(x) = F(x), вероятность безотказной работы R(x) = 1 — F(x).

Вычисление интегралов заменяют использованием таблиц нормального распределения, в которых Мх = 0 и? = 1 (см. табл. П6.1 приложения 6). Для этого распределения функция плотности вероятности имеет одну переменную t и выражается зависимостью.

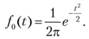
Величина t является центрированной (так как Мt = 0) и нормированной (так как? t = 1). Функцию распределения соответственно можно записать в виде.

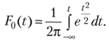(4.2).

Из уравнения (4.2) следует, что F0(t) + F0(-t) = 1, или F0(-t) = 1-F0(t).

При использовании табл. П6.1 приложения 6 в формулу (4.2) вместо t следует подставить значение.

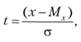
при этом t называют квантилем нормированного нормального распределения (в литературе часто обозначают ир).

Плотность распределения и вероятность отказа соответственно равны f(x) = f0(t)/? и Q(x) = F0(t). Тогда вероятность безотказной работы R(x) = 1 — f0(t), где f0(t) и F0(t) определяют по таблицам^[1].

В работах по надежности часто вместо интегральной функции распределения F0(t) используют функцию Лапласа.

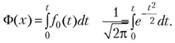
Очевидно, что.

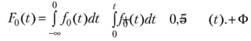
Вероятности отказа и безотказной работы, выраженные через функцию Лапласа:

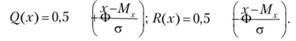
Вероятность попадания случайной величины X в заданный интерват значений от, а до? вычисляют по формуле.

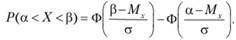(4.3).

Пример 4.3.

Определить вероятность безотказной работы в течение t = 2 • 104 ч ротора механического устройства, если ресурс по износу подчиняется нормальному закону распределения с параметрами М, — 4 • 104 ч;? = 104 ч.

Решение

Находим квантиль:

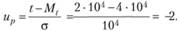
Используя данные табл. П6.1 приложения 6, определяем, что R(t) = = 0,0228.

Ответ: R(t) = 0,0228.

Пример 4.4.

Пусть случайная величина X представляет собой предел текучести кремния. Опытные данные показывают, что предел текучести имеет нормальное распределение с параметрами М, = 650 МПа,? = 30 МПа. Найти вероятность того, что слиток кремния имеет предел текучести в интервале 600−670 МПа.

Решение

Для определения искомой вероятности воспользуемся формулой (4.3):

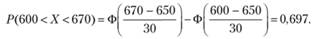
Ответ: 0,697.

Пример 4.5.

Случайная величина X распределена по нормальному закону и представляет собой ошибку измерения датчика давления. При измерении датчик имеет систематическую ошибку в сторону завышения измеряемого значения давления на 0,5 МПа, среднее квадратическое отклонение ошибки измерения составляет 0,2 МПа.

Найти вероятность того, что отклонение измеряемого значения от истинного не превзойдет по абсолютной величине 0,7 МПа.

Решение

По формуле (4.3) с использованием данных табл. П6.1 приложения 6 определим.

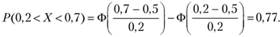
Ответ: Р(Х) = 0,77.

• [1] См. приложение 6 и работу: Оуэн Д. Б. Сборник статистических таблиц. М.: Вычислительный центр ΛΗ СССР, 1973.