Фактор времени в финансовых операциях

Развиваемые компетенции:

знать

• • концепцию временной стоимости денег;
• • методы, используемые для учета фактора времени в долгосрочных финансовых операциях;

уметь

• производить расчеты величины денежных потоков;

владеть

• методами учета фактора времени в финансовых операциях.

Концепция временной стоимости денег

В условиях рыночной экономики при проведении финансовых операций важнейшую роль играет фактор времени.

• «Золотое» правило бизнеса гласит: рубль, полученный сегодня, больше рубля, полученного завтра Проиллюстрируем это ключевое правило бизнеса с помощью следующего примера.

Пример 8.1. Предположим, что некто X обладает суммой 10 000 ден. ед. в момент времени ¢=0 (например, сегодня) и с достоверностью получит еще столько же в момент времени t=1 (например, завтра или через год). Кроме того, существует беспрепятственная возможность положить деньги в банк на этот период либо получить кредит на такой же срок. Банковская ставка по обеим операциям 10%.

Определите величину максимально возможного объема потребления X в текущем и будущем периоде.

Пусть St — сумма, которой обладает X в соответствующем периоде t; Сt — сумма, направленная на потребление в периоде V, r — процентная ставка по банковским операциям.

Наиболее простым считается случай, если X предпочитает полностью тратить свои денежные средства в соответствующем периоде. Определим величину максимально возможного потребления для периодов t = 0 и t = 1 при таких условиях:

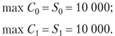
Нетрудно заметить, что суммарное потребление за рассматриваемый период в этом случае.

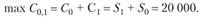
Если же часть полученной в периоде суммы 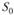будет помещена в банк под 10%, доступные для потребления средства в периоде составят.

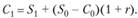
Предположим, что X решил поместить в банк всю сумму 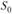, полученную в текущем периоде . Тогда общая сумма, доступная для потребления в период , составит.

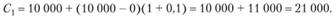
Отметим, что результат соответствует максимально возможному в данном примере общему объему потребления.

При полной гарантии получения 10 000 ден. ед. в периоде t = 1, X может увеличить потребление и в текущем периоде, воспользовавшись возможностью получения кредита в счет будущих доходов. Определим предел объема потребления в текущем периоде. Он будет равен полученному доходу S0 плюс максимальная сумма кредита, которая может быть погашена за счет будущего дохода S1.

Обозначим искомую сумму через у. С учетом платы за кредит в 10% уравнение примет следующий вид:

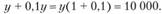
Тогда предельная сумма кредита для X

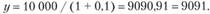
Соответственно максимальный объем потребления для периода 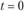составит.

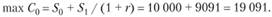
Нетрудно показать, что любые допустимые решения этой задачи будут лежать на прямой, заданной уравнением.

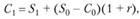
или с учетом заданных значений:

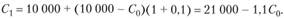
Как следует из полученных соотношений, коэффициент наклона данной прямой равен величине -(1 + r) или -1,1. Однако для нас значительно больший интерес представляет экономическая интерпретация этого показателя, который в данном случае определяет коэффициент обмена текущих денег на будущие и обратно. Другими словами, величина (1 + r) позволяет оценить стоимость денежной единицы в зависимости от времени получения. Нетрудно заметить, что она прямо зависит от значения процентной ставки r.

Так как каждая денежная единица, инвестированная в текущем периоде, дает возможность заработать сумму (1 + r), обладание суммой 5 сегодня эквивалентно обладанию суммой S • (1 + r) в будущем.

Соответственно каждая денежная единица будущих поступлений обладает меньшей ценностью по сравнению с текущей, поскольку отсрочка ее получения лишает возможность заработать в перспективе дополнительный доход в размере (1 + r). Следовательно, она должна стоить меньше текущей на величину (1 + r).

Действительно, в нашем примере обладание суммой S = 10 000 ден. ед. в будущем эквивалентно обладанию суммой S /(1 + r) = 9091 в настоящем, т. е. стоимость будущего рубля при ставке 10% составит 0,9091 коп.

Продемонстрированная неравноценность двух одинаковых по величине (S0 = S1), но разных по времени получения денежных сумм (???0 ф) — явление, широко известное и осознанное в финансовом мире. Его существование обусловлено целым рядом причин. Вот лишь некоторые из них:

• • предпочтение в общем случае индивидуумами немедленного потребления отложенному;
• • имеющаяся в наличии денежная сумма может быть инвестирована и спустя некоторое время принести доход;
• • в реальном мире будущее всегда связано с неопределенностью, поэтому будущие поступления всегда более рисковые, чем текущие;
• • даже при небольшой инфляции покупательная способность денег со временем снижается и др.

Исследования этого явления нашли свое воплощение в формулировке принципа временной стоимости денег (time value of money), который остается краеугольным камнем в современном управлении финансами. Согласно этому принципу сегодняшние денежные поступления ценнее будущих. Соответственно будущие денежные поступления обладают меньшей ценностью, по сравнению с текущими.

Из принципа временно? й ценности денег следуют, по крайней мере, два важных следствия:

• • необходимость учета фактора времени, в особенности при проведении долгосрочных финансовых операций;
• • некорректность (с точки зрения финансового менеджмента) суммирования денежных величин, относящихся к разным периодам времени.

Необходимость учета фактора времени в финансовом менеджменте требует применения специальных методов его оценки.