Бивариативные корреляционные модели

В результате изучения данной главы студент должен:

знать

• • понятия корреляции, ковариации и регрессии;
• • способы вычисления коэффициентов корреляции, ковариации и регрессии для двух переменных;
• • основные положения фиксированной линейной модели корреляционного анализа и ее значение для проверки гипотез о коэффициентах корреляции и регрессии;
• • возможности проверки статистических гипотез о равенстве коэффициента корреляции произвольно заданному значению;
• • возможности сравнения двух коэффициентов корреляции;

уметь

• • оценивать коэффициенты корреляции и строить уравнение простой линейной регрессии аналитическим путем и с помощью статистических пакетов;
• • выдвигать и проверять статистические гипотезы, касающиеся коэффициентов корреляции и регрессии;
• • правильно интерпретировать результаты корреляционного и регрессионного анализа для двух переменных;

владеть

• • базовым понятийным аппаратом корреляционного и регрессионного анализа для двух переменных;
• • навыками «ручной» и компьютерной оценки коэффициентов корреляции и регрессии.

В гл. 3 был рассмотрен простейший однофакторный экспериментальный план, в котором каждое значение зависимой переменной приобретается независимо от другого. Однако такой экспериментальный план слишком неэкономен. Очень часто в эксперименте требуется сократить число испытуемых так, чтобы каждый из них давал не одно, а несколько значений зависимой переменной. В этом случае используется экспериментальный план со связными (зависимыми) выборками. Особенности такого плана, который также называется планом с повторными измерениями, были рассмотрены в гл. 4. Было выяснено, что в таком экспериментальном плане общая дисперсия включает в себя уже не два, а три источника: эффект экспериментального воздействия, эффект испытуемого и эффект экспериментальной ошибки. Для того чтобы извлечь эффект испытуемого из анализа, необходимо оценить меру зависимости данных в повторном измерении. Это же требование присутствует и в более сложных факторных экспериментальных планах, если повторение осуществляется по одной или нескольким независимым переменным.

При этом, как отмечалось, такое требование может быть реализовано с помощью оценки корреляции и ковариации связных значений или переменных. В этой главе познакомимся с данными понятиями более детально.

Статистическая связь признаков

Корреляция

Начнем рассмотрение новых теоретических понятий с анализа конкретного примера (J. Cohen et al. [21]). Предположим, что в эксперименте с помощью специально разработанных психодиагностических процедур оценивалось развитие у детей вербальных и арифметических способностей. Возможные результаты такого эксперимента представлены в табл. 7.1.

В крайней левой колонке табл. 7.1 приведен список испытуемых, участвовавших в эксперименте. Этот список мог бы содержать конкретные имена испытуемых, однако, поскольку сами эти имена не представляют какого-либо значительного интереса для экспериментатора, они часто заменяются условными номерами или иными условными обозначениями испытуемого. В двух других колонках табл. 7.1 приведены результаты каждого испытуемого в тестовых баллах. Как видно, результаты, но арифметическому тесту находятся в определенном соотношении с результатами по вербальному тесту. Так, минимальный результат по обоим тестам демонстрирует испытуемый № 1 — 5 баллов по вербальному тесту и 12 баллов — по арифметическому; максимальный результат опять же по обоим тестам демонстрирует испытуемый № 9 — 10 и 20 баллов соответственно. Испытуемые со средними результатами по вербальному тесту, как правило, демонстрируют средние результаты по арифметическому тесту.

Оказывается, результаты, приведенные в табл. 7.1, могут быть представлены и более наглядно — в виде графика. Для этого будем откладывать по горизонтальной оси координат значения переменной X, по вертикальной оси — значения переменной Y. Таким образом, результат каждого испытуемого будет представлять собой точку на координатной плоскости, а данные по всем испытуемым — как бы поле значений, которое принято называть корреляционным полем. Результаты такого рода работы представлены на рис. 7.1. Такое графическое представление данных принято называть диаграммой рассеивания. Видно, что при возрастании балла, полученного испытуемым, но вербальному тесту, наблюдается аналогичное изменение результата по арифметическому тесту. В таких случаях принято говорить, что связь двух признаков имеет положительный характер. В случае, когда при увеличении значения по одной шкале наблюдается уменьшение значения другой, говорят об отрицательной связи.

Таблица 7.1

Данные, но вербальному и арифметическому тестам для 15 испытуемых дошкольного возраста (адаптировано из работы J. Cohen et al. [21]).

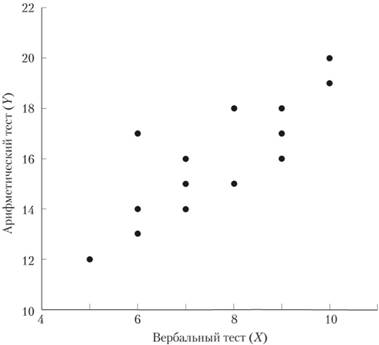
Рис. 7.1. Диаграмма рассеивания.

Кроме того, можно заметить, что выявленная в этом эксперименте связь имеет линейный характер. Однако это соотношение не абсолютно. Имеется тенденция к расположению данных на одной прямой, но в целом данные образуют лишь вытянутое вдоль этой воображаемой прямой облако. Очевидно, чем больше это облако размыто относительной прямой линии, тем меньше связь признаков и наоборот.

Теоретически возможно получить результат, когда связь между двумя признаками не является линейной. В этом случае она может быть монотонной или немонотонной. Монотонной, но нелинейной, является, например, логарифмическая связь признаков. Немонотонной будет связь, описываемая, например, с помощью параболы. В дальнейшем, говоря о статистической связи признаков, будем иметь в виду линейную связь. Это не означает, что нелинейная связь не может быть оценена и выражена с помощью статистических процедур. Просто в данном учебнике мы ее не рассматриваем.

Оценив связь между вербальными и арифметическими способностями на глаз, попробуем теперь их выразить количественно, в виде числа. Нетрудно понять, что основная проблема количественной оценки статистической связи будет заключаться в том, чтобы найти соотносимые между собой единицы измерения.

Как показано в табл. 7.1, балл по тесту арифметических способностей изменяется в диапазоне от 12 до 20, тогда как балл по вербальным способностям изменяется в диапазоне от 5 до 10. Не совсем ясно, насколько возможно сравнение этих данных в исходных единицах. По-видимому, еще большие сложности должны возникнуть, например, при соотнесении между собой роста, выраженного в сантиметрах или дюймах, и веса, выраженного в килограммах или фунтах, хотя совершенно ясно, что и между этими переменными имеется какая-то связь: ведь при увеличении роста должно наблюдаться, по крайней мере, некоторое увеличение веса.

Нельзя, однако, сказать, что такие разнородные величины невозможно вообще сравнивать. В гл. 1, а также в ряде других не раз упоминалась статистическая характеристика, зависящая от исходных величин, но все же позволяющая оценивать связь двух признаков. Эта мера, как мы помним, называется ковариацией. Она по сути является дисперсией, но характеризует распределение не одной, а одновременно двух переменных, и может быть оценена по следующей формуле:

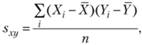(7.1).

где п — объем выборки (число испытуемых в группе).

Так же как и дисперсия, оценка ковариации может быть смещенной или несмещенной. Формула (7.1) представляет собой вариант смещенной оценки. Если необходимо получить несмещенную оценку ковариации, мы можем воспользоваться несколько скорректированной формулой:

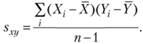
У ковариации как способа оценки статистической связи есть два существенных недостатка. Дело в том, что если статистическая связь между двумя переменными отсутствует, ковариация должна быть равна нулю. Однако обратное неверно: сама по себе связь двух переменных может быть выражена любым числом. К тому же само значение ковариации зависит от выбранного масштаба переменных. Поэтому, например, при оценке ковариации роста и веса мы получим разные ее значения при использовании в качестве меры роста сантиментов и дюймов, а в качестве меры веса — килограммов и фунтов.

Именно поэтому стоит все же перевести имеющиеся у нас данные в сопоставимые величины, например, выразить их в единицах стандартного отклонения. И тогда мера связи, которую мы получим в итоге, никак не будет зависеть от исходных шкал измерения. Такой способ линейной трансформации первоначальной шкалы результатов известен как способ нормализации данных.

Обозначим результат, который получил первый испытуемый по тесту арифметических способностей, как X1, а результат, который получил этот же испытуемый по тесту вербальных способностей, — Y1. Аналогично результаты десятого испытуемого по этим тестам могут быть обозначены соответственно — X10 и Y10. В общем случае будем обозначать результат, полученный г-м испытуемым, но одному тесту, — Xi, а его же результат по другому тесту — Yi. Чтобы соотнести между собой значения X и Y, необходимо перевести их в сопоставимые величины, например, выразить исходные значения X и Y в единицах стандартного отклонения. Для этого воспользуемся линейной трансформацией X и Y в z-величины. Смысл такой трансформации будет состоять в том, чтобы из каждого исходного значения X или Y извлечь среднее арифметическое по выборке и разделить полученные таким образом значения на величины стандартного отклонения. Формально эти манипуляции будут выражаться следующими соотношениями:

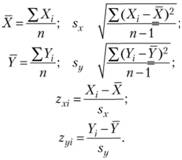
Теперь результат i-го испытуемого по тесту арифметических способностей будем обозначать zxi, его же результат по тесту вербальных способностей — zyi. Эти данные показывают, на сколько единиц стандартного отклонения результаты i-го испытуемого по этим тестам отличаются от среднего арифметического результатов по данным выборкам.

Как нетрудно убедиться, проведенная линейная трансформация исходных значений не изменила структуры полученных данных. Но теперь данные по X и по Y легко могут быть соотнесены друг с другом. Ясно, что если бы в эксперименте была обнаружена абсолютная линейная положительная связь между двумя рассматриваемыми признаками, то любое изменение гх в сторону увеличения или уменьшения должно было бы приводить к аналогичному изменению zy Иными словами, в этом случае для каждого испытуемого значения zx и zy должны быть одинаковыми, а суммарная разность между zx и zy, следовательно, должна равняться нулю. С другой стороны, чем больше различий между 2-значениями х и у и чем больше суммарная разность между ними, тем меньше связь между исходными переменными. Однако по некоторым теоретическим соображениям лучше оценивать не суммарную разность между 2-величинами ?, а сумму квадратов таких разностей 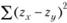. Тогда при оценке статистической связи двух признаков можно воспользоваться следующей формулой:

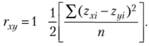(7.2).

Если необходимо оценить статистическую связь двух переменных в генеральной совокупности, то представленная формула будет иметь следующий вид:

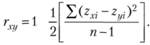(7.3).

Величина r в уравнениях (7.2) и (7.3) представляет собой коэффициент корреляции. В честь английского математика К. Пирсона, впервые предложившего эту формулу в конце XIX в., этот коэффициент еще принято называть коэффициентом корреляции Пирсона.

Коэффициент корреляции является количественной мерой, отражающей величину статистической связи между двумя переменными. Он может изменяться лишь в определенных пределах, а именно, от -1 до +1. Если коэффициент корреляции равен нулю, это означает отсутствие связи двух признаков, т. е. их статистическую независимость. В этом случае на диаграмме рассеивания мы наблюдаем случайное распределение точек по всей плоскости диаграммы. Чем больше коэффициент корреляции отличается от нуля в ту или иную сторону, тем больше связь признаков. Корреляционное поле становится все более вытянутым, постепенно превращаясь в прямую.

Знак корреляции означает характер связи. Положительное значение коэффициента корреляции означает, что при возрастании X соответственно увеличивается значение Y, отрицательное значение свидетельствует о том, что при увеличении X происходит соответствующее уменьшение У. Если коэффициент корреляции оказывается равным +1, связь между переменными оказывается абсолютной, так что одна переменная дублирует другую. Столь же абсолютной является связь двух переменных в случае, когда коэффициент корреляции равен -1. В этом случае в корреляционном поле все данные располагаются на одной прямой.

Таким образом, знак корреляции указывает не на силу связи, а лишь на ее характер. Чем больше коэффициент корреляции отличается от нуля, тем сильнее связь. Поэтому, например, коэффициент корреляции, равный -0,72, обозначает более сильную связь, чем коэффициент корреляции, равный +0,36.

Если попытаться оценить величину коэффициента корреляции Пирсона для нашего случая, можно обнаружить, что он окажется равным 0,82. Однако не стоит торопиться с расчетами.