Иммунизация портфеля из облигаций

Иммунизация портфеля — техника формирования портфеля, позволяющая получить к заданному времени необходимую стоимость портфеля независимо от изменения процентных ставок.

Сама техника довольно проста. В ее основе лежит равенство дюрации портфеля облигаций дюрации обязательств. Например, если вы должны заплатить некоторую сумму одним платежом через два года, то дюрация этого обязательства (в соответствии с правилом 1) равна двум годам. Следовательно, чтобы портфель был иммунизированным, необходимо, чтобы его дюрация также равнялась двум годам.

Дюрация портфеля является средневзвешенной дюрацией отдельных облигаций, входящих в его состав:

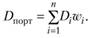(3.18).

В уравнении (3.18) дюрация является либо модифицированной дюрацией, либо дюрацией Маколея, а вес соответствующей бумаги определяется как суммарная стоимость этих бумаг (если она не одна) к суммарной стоимости портфеля на момент формирования. Поясним, почему в уравнении (3.18) неважно, какая используется дюрация. Модифицированная дюрация отличается от дюрации Маколея только множителем, а уравнение можно умножать и делить на любое число, отличное от нуля. Таким образом, главное, чтобы справа и слева были одинаковые дюрации: либо обе модифицированные, либо дюрации Маколея.

Уравнение (3.18) позволяет найти веса каждой бумаги в иммунизированном портфеле, поскольку мы знаем как дюрации отдельных бумаг, так и требуемую дюрацию портфеля.

Изначально в уравнении (3.18) подразумевается условие 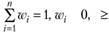т. е. для формирования такого портфеля можно использовать только собственные средства, без привлечения заемных. Кроме того, из уравнения (3.18) следует тот факт, что для формирования подобного портфеля необходимо включение в портфель бумаг с дюрацией, меньшей и большей необходимой дюрации. В противном случае требуемая дюрация при заданных условиях никогда не будет достигнута.

Иммунизация портфеля при этом достигается за счет того, что при изменении процентных ставок стоимость купонов, получаемых по облигациям, меняется ровно на величину изменения стоимости самих облигаций. При этом при росте ставок стоимость купонов растет, а стоимость облигаций падает, а при падении ставок стоимость купонов падает, а стоимость облигаций растет. Таким образом, в иммунизированном портфеле содержатся две силы, изменяющиеся всегда разнонаправленно, причем изменения по модулю равны. Последнее достигается специальным подбором весов бумаг, а значения весов облигаций в портфеле зависят от их дюрации.

Пример 3.13. Фонду HCRV необходимо через два года заплатить 500 000 долл, по контракту. Аналитики рынка планируют увеличение волатильности процентных ставок, поэтому уже через год ставки могут как упасть на один процентный пункт, так и возрасти на такую же величину по сравнению с текущими 10%. Чтобы минимизировать риск неплатежа, фонд решает создать такой портфель из имеющихся двух облигаций, чтобы к моменту осуществления платежа иметь необходимую сумму. Рассчитайте параметры данного портфеля и убедитесь в том, что желаемый результат будет получен. Облигация А: номинал 1000 долл., купонная ставка 8% с годовыми выплатами, текущая доходность к погашению равна 10% при сроке до погашения три года. Облигация Б: номинал 1000 долл., купонная ставка 7% с годовыми выплатами, текущая доходность к погашению 10% при сроке до погашения один год.

Решение

Для защиты стоимости портфеля от параллельного изменения кривой доходности (когда все ставки падают или растут на одну и ту же величину) используют технику иммунизации. Основной принцип построения иммунизированного портфеля: дюрация этого портфеля должна совпадать с дюрацией обязательства. Дюрация единственного платежа совпадает с его сроком. Поэтому дюрация нашего портфеля должна составлять ровно два года.

Для начала рассчитаем текущие стоимости облигаций. Облигация, А стоит 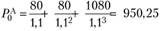долл., а облигация 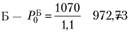долл. Рассчитав дюрации Маколея для обеих облигаций (см. пример 3.11), составим портфель с дюрацией в два года. Дюрация облигации, А равна 2,78 года, а облигации Б — 1 год. Так как дюрация портфеля равна средневзвешенной из дюраций облигаций, в него входящих, то решаем уравнение следующего вида (долю х вкладываем в одногодичные облигации, а сумма долей равна единице):

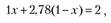
откуда .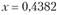

Всего денег в настоящий момент на формирование необходимого нам портфеля понадобится 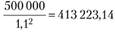долл., при этом в облигации, А необходимо вложить 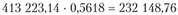долл., а в акции Б — 181 074,38 долл. Таким образом, портфель формируем из 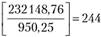облигаций, А и облигаций Б, т. е. на сумму, равную только 950,25 • 244 + 972,73 • 186 = 412 788,78 долл., следовательно, неиспользованными остаются 434,36 долл, в виде наличности, которые можем просто держать в банке под среднерыночный процент.

Таким образом, мы сформировали иммунизированный портфель. Давайте в этом убедимся. Предположим, что если все хорошо, то процентные ставки не поменяются и останутся на уровне 10% годовых. Также рассмотрим два сценария: 1) через год процентные ставки упадут до 9% годовых; 2) через год процентные ставки поднимутся до 11% годовых. Наши предположения представлены на схеме (рис. 3.8).

Рис. 3.8. К примеру 3.13.

Сформируем портфель и определим источники дохода, но нему. Таких источников четыре:

• — 244 облигации А, которые можно продать в нужный момент;
• — 186 облигации Б, которые можно продать в нужный момент;
• — купоны от облигаций А, которые можно реинвестировать;
• — наличность в банке, которую можно снять со счета в нужный момент.

Для каждого сценария ниже приводятся расчеты стоимости портфеля в разрезе каждого из источников (в долл.):

Таким образом, стоимость портфеля составляет всегда требуемую сумму, что бы ни случилось с процентными ставками, другими словами, сформированный портфель является иммунизированным. Сумма незначительно больше требуемой получается вследствие невозможности покупки дробного количества облигаций, чтобы не оставалось свободных денежных средств.

Рассмотренная техника иммунизации пригодна лишь для случая изменения всех ставок на одну и ту же величину (параллельный сдвиг кривой доходности). Для непараллельных сдвигов кривой доходности также существуют техники иммунизации, но они являются более сложными и обычно рассматриваются в специализированных учебниках по управлению портфелем.