Проверка статистических гипотез

В статистическом анализе данных мы всегда имеем дело со случайными переменными, а значит, с вероятностями. Рассчитывая параметр распределения или характеристику связи переменных, мы на самом деле получаем не одну, а две оценки. Первая из них отражает интересующее нас статистическое свойство совокупности объектов, а вторая, не менее важная, показывает степень надежности полученного результата. Сомнения тоже поддаются измерению, и в этой главе мы покажем, как рассчитать меру уверенности в закономерном характере статистических оценок политического мира.

Стандартное нормальное распределение

Стандартное нормальное распределение — очень важный практический инструмент, широко используемый как в анализе данных, так и в создании измерительных методик для политической науки. Умение работать с ним необходимо и для установления степени точности статистических оценок, и для анализа связей между переменными, и для построения индексов.

Начнем с математического определения. Стандартное нормальное распределение — это распределение, подчиняющееся нормальному закону (3.39) с параметрами.

Таким образом, центром (средним значением) стандартного нормального распределения является ноль, а дисперсия и стандартное отклонение равны единице. Другими словами, переменные, обладающие стандартным нормальным распределением, колеблются вокруг нуля, в среднем отклоняясь от него на единицу. Будучи приведенными к стандартному виду, величины становятся сопоставимыми за счет общности параметров распределения.

Первым шагом в стандартизации переменной является центрирование — представление вариации переменной через ее отклонения от среднего значения'.

С помощью операции центрирования достигается выполнение условия (5.1) — центром распределения становится ноль.

Вторым шагом является нормировка (нормирование) — деление всех центрированных значений переменной на ее стандартное отклонение:

Таблица 5.1

Полученные величины называются центрированнонормированными или (чаще в английской литературе) г-баллами. Процедура приведения переменных к такому виду часто носит название ^-преобразования. Объединяя (5.3) и (5.4), получаем общую формулу:

Рассмотрим вычисление стандартного нормального распределения на практическом примере, используя данные российских президентских выборов 2008 г. в разрезе субъектов Федерации (табл. 5.1; файл доступен по ссылке http:// polit.msu.ru/kaf/lab_quant/). Проведем z-преобразование сразу для двух переменных — электоральной поддержки Д. Медведева (ДМ, %) и электоральной поддержки В. Жириновского (ВЖ, %).

Упражнение 5.1

1. Проверьте распределения переменной, воспользовавшись опцией «Гистограмма» в надстройке «Анализ данных» (рис. 5.1а, б).

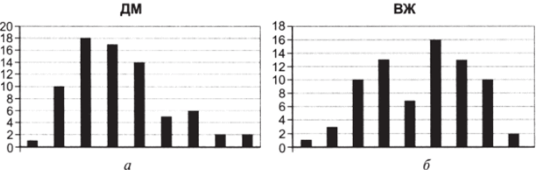
Рис. 5.1.

В целом распределения близки к нормальным.

2. Постройте график вариации переменных ДМ и ВЖ (рис. 5.2). Для этого воспользуйтесь опцией «Вставка — диаграмма — график».

Очевидно, сейчас две переменные значительно различаются как своими средними, так и показателями вариации. Зафиксируем этот факт количественно.

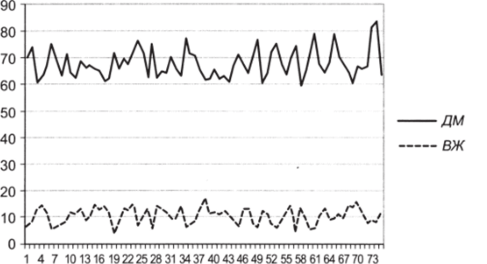
Рис. 5.2.

• 3. Используя функцию «=СРЗНАЧ», рассчитайте средние арифметические переменных в ячейках D2 и Е2. Они равны соответственно 67,77% и 10,44% (округляя до второго знака после запятой). В ячейках D3 и ЕЗ вставьте функции «=D2» и «=Е2» соответственно и растяните до последней строки. Благодаря такой операции в каждой строке будет значение среднего арифметического (рис. 5.5; функции показаны для переменной ДМ для переменной ВЖ все операции осуществляются таким же образом).
• 4. По аналогии с п. 3, рассчитайте в столбцах F и G стандартные отклонения переменных (функция «=СТАНДОТКЛОН»), Они составляют 5,41% для ДМ и 3% для ВЖ.
• 5. Центрируйте переменные по формуле (5.3), вычитая из каждого значения переменной соответствующее среднее.
• 6. Постройте графики центрированных переменных (рис. 5.3).

Теперь обе величины колеблются вокруг единого центра, равного нулю.

• 7. Нормируйте переменные (5.4), разделив центрированные значения на стандартные отклонения.
• 8. Постройте графики центрированно-нормированных переменных (рис. 5.4).

Величины колеблются вокруг нуля, отклоняясь от него в среднем на 1. В таком виде они являются сопоставимыми.

9. Проверьте последнее утверждение, рассчитав средние арифметические и стандартные отклонения полученных переменных.

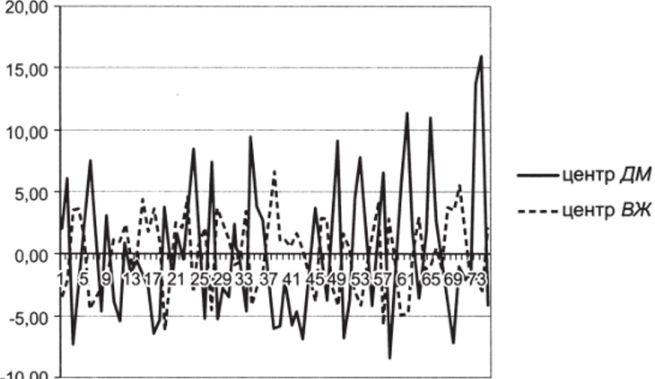
Рис. 5.3.

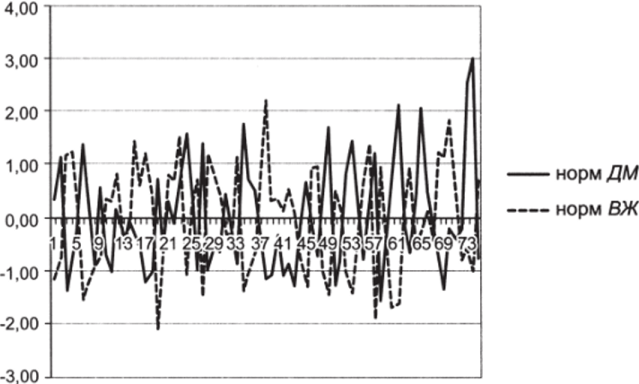
Рис. 5.4.

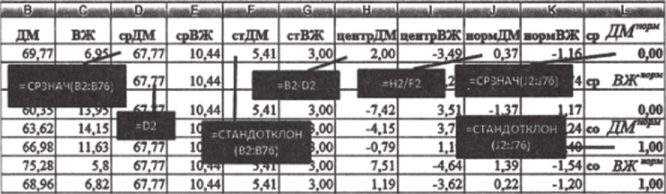
Рис. 55.

Стандартное распределение переменной отличается от ее исходного распределения только своими параметрами — средним и стандартным отклонением. В структурном смысле они идентичны.

10. Постройте гистограммы z-переменных ДМ и ВЖ и сравните их с рис. 5.1а, б. Относительная высота столбцов не изменилась (рис. 5.6а, б).

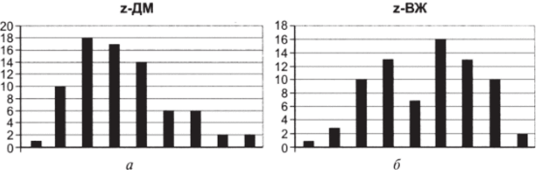
Рис. 5.6.

Еще раз проясним содержательную нагрузку центрированно-нормированных значений переменных, или z-баллов. Так, если электоральная поддержка Владимира Жириновского в Амурской области после z-преобразования составила 1,24, это означает, что в данном регионе результат лидера ЛДПР превышает его средний результат на 1,24 стандартных отклонения. В Брянской области (-0,9) результат В. Жириновского на 0,9 стандартных отклонения ниже по сравнению с его среднероссийским показателем поддержки.

Кроме обеспечения сопоставимости переменных, переход к z-распределению дает еще одну очень важную практическую возможность. Теперь мы можем оценивать вероятности появления значений величин в различных диапазонах, используя стандартные инструменты. К таким инструментам относится прежде всего таблица вероятностей нормального распределения, с помощью которой можно сопоставить z-балл и вероятность того, что величина примет значение меньше заданного — X < х. Другими словами, это функция нормального распределения вероятностей, заданная в табличной форме. Ниже мы приводим фрагмент таблицы нормального распределения для значений z от нуля до одного.

Покажем, как «устроена» эта таблица. В первом столбце даны значения z до первого знака после запятой включи;

тельно (выделены полужирным шрифтом). Выбор нужного значения определяет выбор строки. Как только выбрана строка, в столбцах таблицы мы ищем значение второго знака после запятой, — они приведены в первой строке и также выделены полужирным шрифтом. Как только выбран номер строки и номер столбца, мы получаем искомое значение вероятности.

В нашем примере электоральная поддержка В. Жириновского во Владимирской области составила 11,53%, что соответствует z-значению 0,36; z-значения можно брать из упражнения 5.1 или рассчитывать по формуле (5.5).

Определим вероятность того, что поддержка лидера ЛДП Р будет меньше 0,36. Первому знаку после запятой (0,3) соответствует пятая строка, второму знаку (0,06) — восьмой столбец. На пересечении получаем вероятность 0,64.

Таблица 5.3

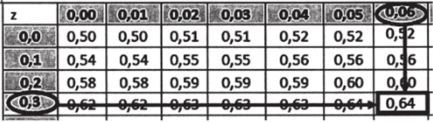
На рис. 5.7 это число соответствует заштрихованной площади под кривой плотности вероятности.

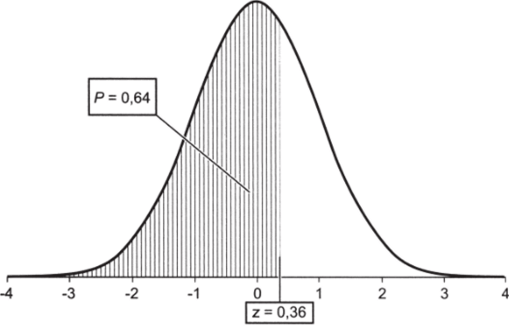
Рис. 5.7.

Другой инструмент, которым мы можем воспользоваться в данном случае, — функция «=НОРМРАСП» в программе Excel. Она находится в разделе «Статистические функции». Чтобы воспользоваться данной функцией, необходимо задать следующие аргументы:

• • значение переменной. В нашем примере это результат лидера ЛДПР во Владимирской области — 11,53%;
• • среднее арифметическое. Для В. Жириновского по взятому нами набору регионов оно составляет 10,44%;
• • стандартное отклонение. Как и среднее, мы рассчитывали его в рамках центрирования и нормировки; оно составляет 3%;
• • «Интегральная» — логическое значение, определяющее вид функции распределения. Нужно указать в этом поле значение «Истина» (рис. 5.8).

Для тренировки расчета вероятностей мы рекомендуем пользоваться табличными значениями, а функцию «=НОРМРАСП» использовать в качестве проверочного инструмента.

Теперь выясним, какова вероятность того, что поддержка главы ЛДПР на выборах 2008 г. окажется выше, чем 12,86%.

Рис. 5.8.

(результат в Вологодской области). Для данного уровня поддержки z-значение составляет 0,81. Табличное значение вероятности — 0,79 (десятая строка и третий столбец табл. 5.2). Но табличное значение дает нам вероятность того, что результат окажется ниже заданного, а это не то, что требуется в данном случае. Чтобы решить эту проблему, необходимо вспомнить формулу (3.12), в соответствии с которой площадь под кривой плотности вероятности всегда равна единице. Следовательно, вероятность того, что поддержка будет выше какого-то определенного значения, равна:

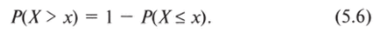
В нашем примере.

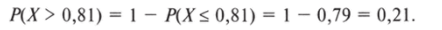
Эта вероятность соответствует площади под кривой справа от указанного значения (рис. 5.9).

Теперь рассчитаем вероятность того, что поддержка В. Жириновского окажется меньше 7,73% (результат в Брянской области). Соответствующее z-значение равно -0,9. Так как в этом регионе лидер ЛДПР получил результат ниже своего среднего по России показателя, z-значение отрицательное; в таблице же указаны только положительные.

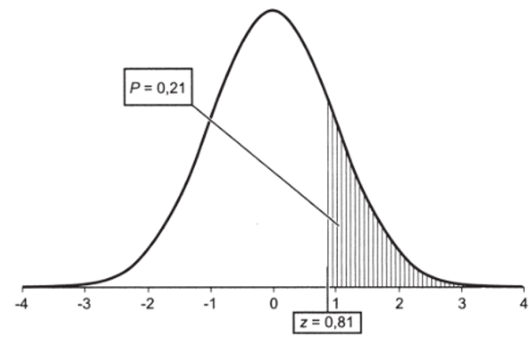
Рис. 5.9.

значения. Эту трудность мы преодолеем, используя замечательное свойство кривой плотности вероятности нормального распределения: она симметрична относительно центра. Поэтому сначала найдем по таблице вероятность того, что В. Жириновский получит результат меньше 0,9. В одиннадцатой строке и втором столбце табл. 5.2 находим значение 0,82. Затем определим вероятность того, что электоральная поддержка лидера ЛДПР будет больше 0,9. Как и в предыдущем примере, воспользуемся вычитанием из единицы:

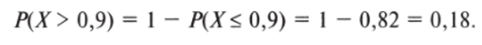
Так как кривая симметрична, справедливо следующее равенство:

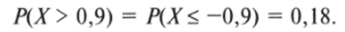
Таким образом, мы ответили на поставленный вопрос. Вероятность того, что на выборах 2008 г. лидер ЛДПР получает результат меньше, чем в Брянской области (или равный ему^[1]), составляет 0,18.

Графически последовательность действий представлена на рис. 5.10.

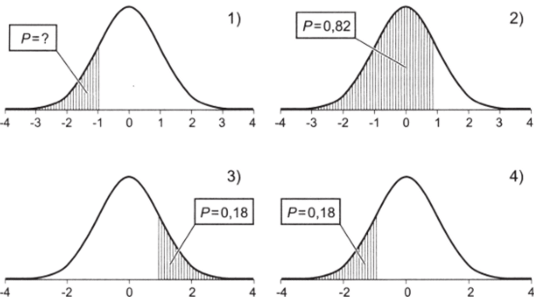
Рис. 5.10.

Наконец, рассчитаем вероятность того, что результат В. Жириновского на выборах 2008 г. окажется в интервале между показателями его поддержки в Воронежской (8,95%) и Калининградской (11,67%) областях:

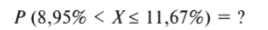
• 1. Дая нижней границы интервала z-значение составляет -0,49.
• 2. Найдем по таблице вероятность Р (Х < 0,49) = 0,69.
• 3. Рассчитаем Р (Х> 0,49) = 1 — Р (Х< 0,49) = 1 — 0,69 = 0,31.
• 4. За счет симметрии «колокола» получаем Р (Х > 0,49) = = Р{Х< -0,49) = 0,31.

Наш промежуточный результат выглядит следующим образом (рис. 5.11).

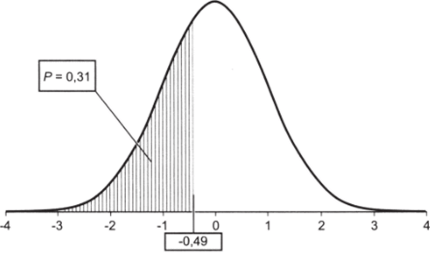
Рис. 5.11.

• 5. Для верхней границы интервала (11,67%) z-значение составляет 0,41.
• 6. Найдем по таблице вероятность Р{Х < 0,41) = 0,66.
• 7. Рассчитаем Р (Х> 0,41) = 1 — Р (Х < 0,41) = I — 0,66 = = 0,34.

Результат действий 5—7 см. на рис. 5.12.

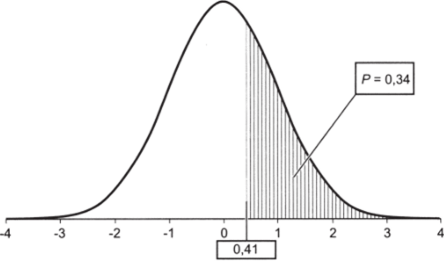
Рис. 5.12.

Итак, нам известна вероятность попадания значений слева от нижней границы интервала (рис. 5.11) и справа от верхней границы интервала (рис. 5.12). Нас же интересует то, что находится «посередине», — вероятность попадания значений в сам интервал. Вновь используем тот факт, что площадь под кривой плотности вероятности равна единице:

8. 1 — Д-0,49 < Х< 0,41) = 1 — Р (Х< 0,49) — FX> 0,41) = = 1 — 0,31 — 0,34 = 0,35.

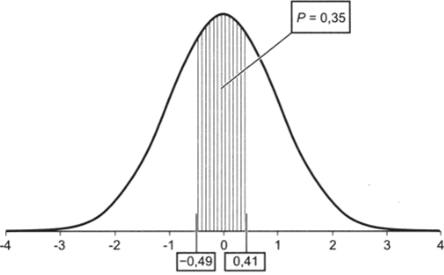
Рис. 5.13.

Итак, вероятность того, что результат В. Жириновского на выборах окажется в интервале между показателями его поддержки в Воронежской области и в Калининградской области, составляет 0,35:

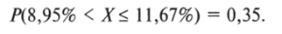
Проведенные нами расчеты позволяют понять основное эмпирическое правило нормального распределения — правило трех сигм. Как уже было отмечено в главе 3, это правило гласит, что для нормально распределенной совокупности в интервал от -1 до 1 стандартного отклонения от среднего значения попадают 68,3% всех значений, в интервал ±2 стандартных отклонения — 95,4% всех значений и, наконец, в интервал ±3 стандартных отклонения от центра — 99,7% всех значений (см. рис. 5.14).

Рис. 5.14.

Это правило, в частности, показывает, насколько редким является отклонение более чем на 2 стандартных отклонения от среднего: такое случается всего в 4—5 случаях из 100.

Проверим это правило для одного стандартного отклонения от среднего, используя алгоритм предыдущего примера.

Нам надо оценить вероятность того, что z-значение попадет в интервал от -1 до 1:

• 1. Найдем по табл. 5.2 вероятность того, что значение будет меньше или равно 1: Р (Х < 1) = 0,84.
• 2. Р (Х>) = 1 — 0,84 = 0,16.
• 3. Р (Х 1) = 0,16.
• 4. Л-1 < Х< 1) = 1 — Р (Х> 1) — FX< -1) = 1 — 0,16 — - 0,16 = 0,68.

Последнее выражение соответствует утверждению, что в интервал от -1 до 1 стандартного отклонения от среднего попадают примерно 68% всех значений (слово «примерно» возникает здесь потому, что точность таблицы ограничена вторым знаком после запятой).

Самостоятельно проверьте правило трех сигм для ±2 и ±3 стандартных отклонений от среднего.

• [1] В формальной записи используется знак «меньше или равно». Мы, какправило, будем говорить просто «меньше»: вероятность того, что непрерывная величина примет какое-то конкретное значение, равна нулю.