Статистическая проверка гипотез о параметрах генеральной совокупности

Мощность критерия равна вероятности того, что выборочная характеристика (статистика) критерия попадет в критическую область, когда #0 ложна, т. е. 1 — Р = P (fl |Я,). Обычно при проверке гипотезы уровень значимости, а (вероятность ошибки первого рода) выбирают достаточно малым (0,05 или 0,01). Затем для конкретных гипотез — нулевой #0 и альтернативной Я (- вычисляют мощность критерия 1 — (3… Читать ещё >
Статистическая проверка гипотез о параметрах генеральной совокупности (реферат, курсовая, диплом, контрольная)
Статистическая проверка гипотез для одномерной совокупности
- • гипотеза H0 верна, и се принимают согласно критерию;
- • гипотеза H0 неверна, и ее отвергают согласно критерию;
- • гипотеза H0 верна, но ее отвергают согласно критерию (ошибка первого рода),
- • гипотеза H0 неверна, но ее принимают согласно критерию (ошибка второго рода).
Уровнем значимости а называют вероятность совершить ошибку первого рола, т. е. ошибку, заключающуюся в том, что проверяемая статистическая гипотеза H() отклоняется в то время, как она верна, т. е. ошибка первого рода равна вероятности того, что выборочная характеристика (статистика) критерия попадет в критическую область, когда H0 верна (рис. 2.3).
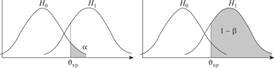
Рис. 2.3. Уровень значимости, а и мощность критерия 1 — Р.
С уменьшением, а возрастает вероятность ошибки (3 второго рода: принять Н{), когда она неверна.
Мощностью критерия называют вероятность отклонения нулевой гипотезы Я0, когда она неверна, т. е. вероятность 1 — (3 не совершить ошибку второго рода.
Мощность критерия равна вероятности того, что выборочная характеристика (статистика) критерия попадет в критическую область, когда #0 ложна, т. е. 1 — Р = P (fl |Я,). Обычно при проверке гипотезы уровень значимости, а (вероятность ошибки первого рода) выбирают достаточно малым (0,05 или 0,01). Затем для конкретных гипотез — нулевой #0 и альтернативной Я (- вычисляют мощность критерия 1 — (3, которая очень часто получается значительно меньше желаемого значения. В этом случае осторожно говорят, что Я0 не отвергается, что она не противоречит результатам наблюдений. Приняв в этом случае гипотезу Я0, можно с достаточно большой вероятностью р совершить ошибку второго рода.
Обозначим через Р (0* е WH) вероятность попадания статистики критерия 0* в критическую область IV, если верна гипотеза Я.
Тогда требования к критической области аналитически можно записать так:
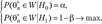 (2.18).
(2.18).
где второе условие выражает требование максимума мощности критерия.
Из условий (2.18) следует, что критическая область выбирается так, чтобы вероятность попадания в нее была бы минимальной (равной а), если верна нулевая гипотеза Я0, и максимальной — в противоположном случае.
В зависимости от вида конкурирующей гипотезы выбирают правостороннюю, левостороннюю или двустороннюю критические области. Границы критической области при заданном уровне значимости, а находят из соотношений:
- • для правосторонней критической области Р (в'" > 0кр) = а;
- • для левосторонней критической области /'(О* < 9кр) = а;
- • для двусторонней симметрической области Р (в'п > 0кр пр) = а/2, Р (0' < < йкрлсв) = а/2, причем 0крлсв< 0кр
Проверка гипотез о генеральной средней нормальной совокупности. Пусть из генеральной совокупности X, значения признака которой имеют нормальный закон распределения Я (р; ст) с неизвестными математическим ожиданием р и дисперсией а2, взята случайная выборка х, х2 х" объемом п, по данным которой получены среднее арифметическое х и дисперсия выборки S'1, и пусть р0 и р, — определенные нормативные значения признака. Тогда для проверки нулевой гипотезы Я0: р = р () при альтернативной гипотезе Я: р = р (используют статистику 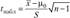 , которая при выполнении гипотезы Я0 имеет распределение Стьюдента (f-распределение) с и — 1 степенями свободы.
, которая при выполнении гипотезы Я0 имеет распределение Стьюдента (f-распределение) с и — 1 степенями свободы.
Согласно статистике при р, > р0 выбирают правостороннюю критическую область, при р, < р0 — левостороннюю, а при конкурирующей гипотезе Яр р = р, * р0 — двустороннюю критическую область, т. е. допускается Р] > ро и р| < р<|. В случае двусторонней критической области конкурирующая гипотеза Я| перестает быть простой, поэтому для этого случая мощность критерия обычно не определяют.
Границы критической области |{"а6д| определяют по таблице {-распределения для заданного уровня значимости, а и числа степеней свободы и — 1.
Границы критической области (fKp) находят по таблице функции {-распределения (5{(fTa6jI;v) = P (|{|>{та6л) = а (v — число степеней свободы)) из условий:
- • в случае односторонней критической области используется условие &({" «; п — 1) = 2а;
- • в случае двусторонней критической области — 5{({кр; п — 1) = а.
Проверка гипотезы сводится к следующему: если |{,^,| > <�кр, то гипотеза отвергается с вероятностью ошибки а, если | txa (a < Гкр, то делают вывод о том, что гипотеза не противоречит опытным данным [19, 23].
Мощность критерия в случае односторонней критической области можно определить по формуле.
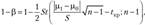 (2.19).
(2.19).
где fKp = St~l(2а; n-1) определяется по таблице {-распределения Стьюдента (см. табл. П2 приложения) для вероятности 2а и числа степеней свободы v = и — 1.
Пример 2.12
По результатам анализа темпов роста производительности на 10 предприятиях отрасли было установлено, что средний темп роста составляет х= 2,5% и S = 0,4%. Предполагая, что темп роста есть случайная величина, распределенная, но нормальному закону, проверим на уровне значимости, а = 0,05 гипотезу Я0: рп = 2,6% против альтернативной гипотезы Я: р, = 2,2% и вычислим мощность критерия.
Решение
В основе проверки гипотезы о значении генеральной средней при неизвестной дисперсии лежит статистика 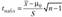 , которая при выполнении нулевой гипотезы имеет распределение Стьюдента (^-распределение) с п — 1 степенями свободы. Наблюдаемое значение статистики равно.
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента (^-распределение) с п — 1 степенями свободы. Наблюдаемое значение статистики равно.

Так как альтернативная гипотеза Я:  >, то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия
>, то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия 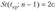 l.
l.
По таблицам-распределения имеем.
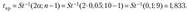
Так как наблюдаемое значение статистики критерия по модулю не превосходит критического фнабл| < гкр), то можно сделать вывод о том, что на уровне значимости, а = 0,05 гипотеза Я0: р0 = 2,6% не противоречит опытным данным.
Мощность критерия проверки гипотезы о значении генеральной средней при неизвестной дисперсии определяется по формуле (2.19):
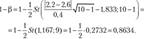
Проверка гипотезы о равенстве генеральных средних двух нормальных совокупностей при неизвестных генеральных дисперсиях. Пусть X и Y- нормальные совокупности с равными, но неизвестными дисперсиями ст;. = aj = а2 и математическими ожиданиями рг и р. Из этих совокупностей взяты две случайные независимые выборки с параметрами х, 5| и у, 5|. На уровне значимости, а требуется проверить нулевую гипотезу Я0: р, =.
В основу критерия для проверки нулевой гипотезы положена статистика.

которая при выполнении нулевой гипотезы Н0 имеет распределение Стьюдента с v = пх + Пу — 2 степенями свободы.
При заданном уровне значимости, а выбор критической области зависит от конкурирующей гипотезы: при Я: р, > р выбирают правостороннюю, при Н: рд.< - левостороннюю, а при Я (: рг^ р" - двустороннюю критические области.
Критерий проверки гипотезы заключается в следующем: если |гиа6л| > гкр, где fKp = 5f1(2a; пх + - 2) (для правосторонней и левосторонней критических областей) или Ск|) = St~'(a пх+ пц — 2) (для двусторонней критической области), то гипотезу отвергают, если же |Тна6л| < tK|), то делают вывод о том, что гипотеза не противоречит опытным данным.
Проверка гипотез о генеральной дисперсии нормальной совокупности. Пусть из генеральной совокупности, значения признака которой распределены, но нормальному закону с неизвестной дисперсией о2, взята случайная выборка из п независимых наблюдений и пусть S2 — выборочная дисперсия.
Требуется проверить нулевую гипотезу //": ст2 = ajj, где crjj — определенное заданное значение дисперсии при заданном уровне значимости а. Для проверки нулевой гипотезы используют выборочную характеристику:
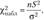
которая при выполнении гипотезы Я0 имеет распределение у2 с п — степенями свободы.
В зависимости от конкурирующей гипотезы выбирают правостороннюю, левостороннюю или двустороннюю критические области. Границы критической области ХкР определяют по таблице распределения у} для заданного уровня значимости а и числа степеней свободы п- 1. Рассмотрим три случая.
1. Если Н. а2 > ajj, то выбирают правостороннюю критическую область и %2р находят из условия.
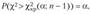 (2.20).
(2.20).
где x2,(a; п — 1) — табличное значение у2, найденное для уровня значимости, а и числа степеней свободы я — 1.
Правило проверки гипотезы следующее: если х2а (;, >ХкР. тн нулевую гипотезу Н0: а2 = отвергают, если Х2.Л:1 S х2р, то нулевая гипотеза не противоречит опытным данным.
Для вычисления мощности критерия можно воспользоваться формулой.
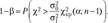 (2.21).
(2.21).
2. Если конкурирующая гипотеза Я: ст2 = af ф ajj, то строят двустороннюю критическую область. Левую (Хкрлсв) и правую (Хкр прав) границы критической области находят из условий.
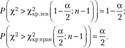 (2.22).
(2.22).
В этом случае правило проверки гипотезы сводится к следующему: если Хкрлсв — Хнабл — Хкрпмв’т0 У нас нет основания отвергнуть гипотезу. Если же Х?, абл ^ правто гипотезу отвергают.
3. При конкурирующей гипотезе Н{: a2=af <�а§ строят левостороннюю критическую область. Границу критической области определяют по таблице распределения у2 (см. табл. 1.13 приложения) из условия.
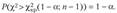 (2.23).
(2.23).
Если  , то гипотеза #0: a2 = ajj отвергается, если же
, то гипотеза #0: a2 = ajj отвергается, если же 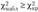 , то гипотеза Я0 не отвергается.
, то гипотеза Я0 не отвергается.
Для вычисления мощности критерия можно воспользоваться формулой.
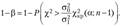 (2.24).
(2.24).
Пример 2.13
По результатам п = 18 независимых измерений найдено, что х = 115 мм, а 5= 0,5 мм. Допустив, что ошибки измерения имеют нормальное распределение:
а) проверим на уровне значимости a = 0,01 гипотезу Я0: = 0,2 мм² против кон;
курирующей гипотезы Я: of = 0,1 мм² и вычислим мощность критерия;
- б) проверим на уровне значимости a = 0,05 гипотезу Я (): о§ = 0,2 мм² против конкурирующей гипотезы Я: of = 0,3 мм² и вычислим мощность критерия;
- в) проверим на уровне значимости а = 0,1 гипотезу Я0: о§ = 0,2 мм² против конкурирующей гипотезы Я: of ф 0,2 мм².
Решение
а) В основе проверки гипотезы о значении генеральной дисперсии лежит статиcтика 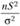 , наблюдаемое значение которой равно
, наблюдаемое значение которой равно 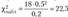 .
.
Так как альтернативная гипотеза 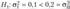 , то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.23).
, то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.23).
По таблицам распределения уы1 (см. табл. ПЗ приложения) имеем  1.
1.
Так как наблюдаемое значение статистики критерия не меньше критического значения, то можно сделать вывод о том, что на уровне значимости а = 0,01 гипотеза Я0: о§ = 0,2 мм² не противоречит опытным данным.
Мощность критерия проверки гипотезы о значении генеральной дисперсии в случае левосторонней критической области определяется по формуле (2.24):

б) Наблюдаемое значение статистики вычисляется аналогично и. а) и равно.

Так как альтернативная гипотеза 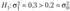 , то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в правостороннюю критическую область, границы которой определяются из условия (2.20). По таблицам распределения
, то гипотеза Я0 отклоняется в пользу гипотезы Я, при попадании статистики критерия в правостороннюю критическую область, границы которой определяются из условия (2.20). По таблицам распределения 
Так как наблюдаемое значение статистики критерия не превосходит критическое значение, то можно сделать вывод о том, что на уровне значимости a = 0,05 гипотеза 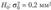 не противоречит опытным данным.
не противоречит опытным данным.
Мощность критерия проверки гипотезы о значении генеральной дисперсии в случае правосторонней критической области определяется по формуле (2.21): 
в) Наблюдаемое значение статистики аналогично предыдущим пунктам равно 
Так как альтернативная гипотеза 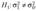 , то гипотеза //, отклоняется в пользу гипотезы Н| при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условий (2.22). По таблицам распределения х2 (см. табл. ПЗ приложения)
, то гипотеза //, отклоняется в пользу гипотезы Н| при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условий (2.22). По таблицам распределения х2 (см. табл. ПЗ приложения) 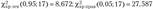
Так как наблюдаемое значение статистики критерия  , то можно сделать вывод о том, что на уровне значимости а = 0,1 гипотеза
, то можно сделать вывод о том, что на уровне значимости а = 0,1 гипотеза  ! мм2 не противоречит опытным данным.
! мм2 не противоречит опытным данным.
Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей. Пусть X и У — генеральные совокупности, значения признаков которых распределены по нормальному закону с дисперсиями 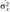 и
и 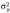 Из этих совокупностей взяты независимые случайные выборки объемом п, и пу, и пусть
Из этих совокупностей взяты независимые случайные выборки объемом п, и пу, и пусть 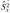 и
и 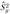 - исправленные выборочные дисперсии, причем
- исправленные выборочные дисперсии, причем 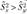
где 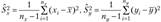
Требуется проверить нулевую гипотезу 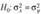 против альтернативной гипотезы
против альтернативной гипотезы 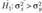 . Основу критерия для проверки нулевой гипотезы составляет статистика.
. Основу критерия для проверки нулевой гипотезы составляет статистика.

которая при выполнении нулевой гипотезы имеет распределение Фишера — Снедекора (Т-распределение) с пх — 1 и пу — 1 степенями свободы.
Для проверки гипотезы выбирают правостороннюю критическую область. Границу критической области Ткр (а; пх — 1; пу — 1) определяют по таблице F-распределения при заданном уровне значимости, а и числе степеней свободы пх- 1 и nt) — 1 из условия.
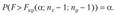
Критерий проверки гипотезы состоит в том, что при выполнении условия  полагают, что гипотеза не противоречит опытным данным; а если
полагают, что гипотеза не противоречит опытным данным; а если 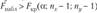 I, то гипотезу отвергают с вероятностью ошибки а.
I, то гипотезу отвергают с вероятностью ошибки а.
Пример 2.14
Для исследования состава работников предприятий были сделаны выборки по 10 предприятиям («j = п2 = 10) и определена доля мужчин в общей численности работников в каждой выборке. Для предприятий первой отрасли средняя доля составила .Vj = 68,2% со стандартным отклонением 5, = 0.7%. для предприятий второй отрасли — х2 = 67.0% с S2 = 0.74%. Имеются ли основания полагать, что состав работников различается в этих двух отраслях?
Решение
Так как проверка гипотезы о равенстве генеральных средних Н0: Mi = И2 основана на условии, что истинные значения генеральных дисперсий неизвестны, но равны (of = о|), то предварительно необходимо проверить гипотезу о равенстве генеральных дисперсий двух совокупностей.
Поэтому сначала проверим гипотезу о равенстве генеральных дисперсийдвух совокупностей, т. е. проверим на уровне значимости, а = 0.05 гипотезу 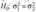 против конкурирующей гипотезы
против конкурирующей гипотезы  В основе проверки гипотезы о значении генеральной дисперсии лежит статистика
В основе проверки гипотезы о значении генеральной дисперсии лежит статистика 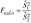 (в предположении о том, что
(в предположении о том, что 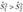 ), которая при выполнении нулевой гипотезы имеет распределение Фишера — Снедекора (^-распределение) с пх - 1 и п2- 1 степенями свободы.
), которая при выполнении нулевой гипотезы имеет распределение Фишера — Снедекора (^-распределение) с пх - 1 и п2- 1 степенями свободы.
Рассчитаем.
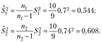
Так как 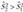 , то наблюдаемое значение статистики равно.
, то наблюдаемое значение статистики равно.
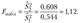
Границы критической области определяются по таблицам распределения Фишера — Снедекора (табл. 114 приложения) из условия 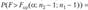 = а, откуда FKp (0,05; 9; 9) = 3.18. Наблюдаемое значение статистики критерия меньше критического значения
= а, откуда FKp (0,05; 9; 9) = 3.18. Наблюдаемое значение статистики критерия меньше критического значения  и можно сделать вывод о том. что различия между дисперсиями двух совокупностей несущественны на 5%-ном уровне значимости. Предположив, что две генеральные дисперсии равны друг другу, перейдем к проверке гипотезы о равенстве генеральных средних, т. е. проверке на уровне значимости, а = 0,05 гипотезы #(): р, = р2 против конкурирующей гипотезы
и можно сделать вывод о том. что различия между дисперсиями двух совокупностей несущественны на 5%-ном уровне значимости. Предположив, что две генеральные дисперсии равны друг другу, перейдем к проверке гипотезы о равенстве генеральных средних, т. е. проверке на уровне значимости, а = 0,05 гипотезы #(): р, = р2 против конкурирующей гипотезы 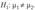 . В основе проверки гипотезы о равенстве генеральных средних (предполагается. что значения генеральных дисперсий неизвестны, но равны) лежит статистика
. В основе проверки гипотезы о равенстве генеральных средних (предполагается. что значения генеральных дисперсий неизвестны, но равны) лежит статистика  , которая при выполнении нулевой гипотезы имеет распределение Стьюдента (^-распределение) с я, + п2- 2 степенями свободы.
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента (^-распределение) с я, + п2- 2 степенями свободы.
Наблюдаемое значение статистики равно.
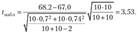
Так как альтернативная гипотеза //: р, * х2, то гипотеза И0 отклоняется в пользу гипотезы //, при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условия St (tKp, и, + п2 — 2) = а. По таблицам-распределения найдем tKp = &-1(0,05; 10 + 10 — 2) = 5f_,(0.05; 18) = 2,1.
Наблюдаемое значение статистики критерия по модулю превосходит критическое (1*набл1 > *кр. поэтому нулевая гипотеза отвергается и можно сделать вывод о том, что состав работников на предприятиях двух отраслей различен.
Проверка гипотез об однородности ряда дисперсий. Критерий Бартлетта. Пусть 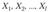 есть / нормальных генеральных совокупностей, из которых извлечены выборки объемом
есть / нормальных генеральных совокупностей, из которых извлечены выборки объемом 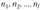 соответственно, и пусть
соответственно, и пусть 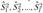 - исправленные выборочные дисперсии.
- исправленные выборочные дисперсии.
Требуется на уровне значимости, а проверить нулевую гипотезу о равенстве дисперсий / генеральных совокупностей, т. е. 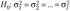
Введем обозначения:
- •
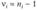 — число степеней свободы г-й выборки;
— число степеней свободы г-й выборки; - •
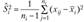 для
для  где
где  — результат j-го наблюдения г-й выборки;
— результат j-го наблюдения г-й выборки; - •
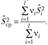
В качестве выборочной характеристики критерия Бартлетт предложил использовать статистику.

где 
При выполнении нулевой гипотезы #0 и при  приближенно имеет распределение
приближенно имеет распределение 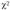 с / - 1 степенями свободы 22.
с / - 1 степенями свободы 22.
Для проверки нулевой гипотезы строят правостороннюю критическую область, границу которой определяют, но таблице распределения 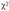 (см. табл. ПЗ приложения) для уровня значимости а и числа степеней свободы / - 1 из условия.
(см. табл. ПЗ приложения) для уровня значимости а и числа степеней свободы / - 1 из условия.
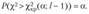
Критерий проверки гипотезы заключается в следующем: если выполняется условие 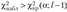 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 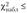
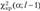 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.
Критерий Бартлетта весьма чувствителен к отклонениям законов распределений Xj для 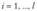 от нормального закона.
от нормального закона.
В случае когда гг, = … = И/, для проверки нулевой гипотезы Я0 используют критерий Кохрана.
Критерий Кохрана. Пусть 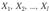 — нормальные генеральные совокупности с неизвестными дисперсиями
— нормальные генеральные совокупности с неизвестными дисперсиями 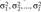 , из которых взяты независимые случайные выборки одинакового объема
, из которых взяты независимые случайные выборки одинакового объема  и пусть
и пусть 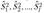 — исправленные выборочные дисперсии соответствующих совокупностей. Требуется проверить нулевую гипотезу Ни:
— исправленные выборочные дисперсии соответствующих совокупностей. Требуется проверить нулевую гипотезу Ни:  С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике.
С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике.
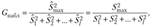
которая при выполнении нулевой гипотезы имеет G-распределение с v = п — 1 степенями свободы и к сравниваемыми совокупностями (табл. 1.19 приложения), где 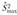 - наибольшая из исправленных выборочных дисперсий.
- наибольшая из исправленных выборочных дисперсий.
Для проверки нулевой гипотезы Нп на уровне значимости, а строят правостороннюю критическую область.
Границу критической области <7К|) находят по таблице G-распределения (см. табл. П9 приложения) из условия.

Критерий проверки гипотезы заключается в следующем: если выполняется условие 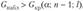 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 
 |, то считают, что гипотеза не противоречит опытным данным.
|, то считают, что гипотеза не противоречит опытным данным.
Проверка гипотез о вероятности в случае биномиального распределения. Пусть рассматривается генеральная совокупность, значения признака которой имеют биномиальный закон распределения с неизвестным параметром р, где р — вероятность появления события А, р0 и р, — определенные значения параметра р. Пусть из этой совокупности берется выборка объемом п, в которой значение признака наблюдалось т раз. Для проверки нулевой гипотезы Н0: р = р() при альтернативной гипотезе Н{р = Р используют при больших значениях выборки (п > 50) статистику.
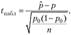
где 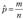 , которая при выполнении нулевой гипотезы имеет нормированное распределение Л'((); 1).
, которая при выполнении нулевой гипотезы имеет нормированное распределение Л'((); 1).
Согласно требованию (2.18) при 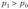 выбирают правостороннюю критическую область, при
выбирают правостороннюю критическую область, при 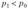 — левостороннюю, а при конкурирующей гипотезе
— левостороннюю, а при конкурирующей гипотезе 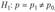 когда допускается
когда допускается 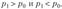 выбирают двустороннюю критическую область.
выбирают двустороннюю критическую область.
Границы критической области (Гкр) находят по таблице интегральной функции Лапласа Ф (г) (см. табл. П1 приложения) из условий:
- • в
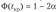 случае правосторонней и левосторонней критических областей
случае правосторонней и левосторонней критических областей - • при двусторонней критической области

Тогда проверка гипотезы сводится к следующему: если |Сна6л| > tKp, то гипотеза отвергается с вероятностью ошибки а, если |гна6л| < гкр, то делают вывод о том, что гипотеза не противоречит опытным данным.
Проверка гипотез об однородности ряда вероятностей. Пусть Xv Х2,… X/ - I генеральных совокупностей, каждая из которых характеризуется неизвестным параметром Рг где Р, — вероятность появления события А в соответствующей выборке.
Требуется по результатам выборочных наблюдений проверить нулевую гипотезу о равенстве вероятностей появления события А в генеральных совокупностях, т. е.  Для проверки гипотезы можно использовать статистику.
Для проверки гипотезы можно использовать статистику.

где 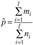 — средняя частость появления события А по всем выборкам.
— средняя частость появления события А по всем выборкам.
Или, переходя к частостям, но всем выборкам 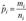 , получим статистику
, получим статистику 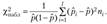
Статистика 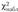 при выполнении нулевой гипотезы имеет асимптотическое распределение
при выполнении нулевой гипотезы имеет асимптотическое распределение 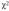 с / - 1 степенями свободы, где / - число генеральных совокупностей.
с / - 1 степенями свободы, где / - число генеральных совокупностей.
Для проверки нулевой гипотезы на уровне значимости, а строят правостороннюю критическую область, границу  которой определяют из условия.
которой определяют из условия.
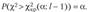
Критерий проверки гипотезы заключается в следующем: если выполняется условие  I, то гипотезу отвергают, если же
I, то гипотезу отвергают, если же 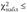
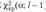 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.
Пример 2.15
Из 100 студентов одного факультета 35 отлично сдали экзамен по высшей математике, из 150 студентов другого факультета отличников оказалось 40. Проверим на уровне значимости, а = 0,02 гипотезу о том, что вероятность отличной оценки не зависит от того, на каком факультете проводится экзамен, т. е 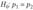
Решение
В основе проверки гипотезы об однородности ряда вероятностей лежит статистика 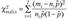 , которая при выполнении нулевой гипотезы имеет распределение
, которая при выполнении нулевой гипотезы имеет распределение 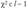 степенями свободы, где I — число сравниваемых совокупностей.
степенями свободы, где I — число сравниваемых совокупностей.
По данным задачи 
Наблюдаемое значение статистики равно.
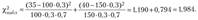
Границы критической области определяются из условия По таблицам распределения 

Так как наблюдаемое значение статистики критерия не превосходит критического значения, то можно сделать вывод о том, что на уровне значимости, а = 0,02 гипотеза 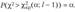 не противоречит опытным данным.
не противоречит опытным данным.
Проверка однородности ряда вероятностей в случае полиномиального распределения. Пусть 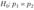 есть / генеральных совокупностей, из которых взяты случайные независимые выборки объемом
есть / генеральных совокупностей, из которых взяты случайные независимые выборки объемом  и пусть Tij элементов г-й выборки классифицируются по какому-либо признаку на h групп с числом элементов в каждой группе
и пусть Tij элементов г-й выборки классифицируются по какому-либо признаку на h групп с числом элементов в каждой группе  где
где 
Очевидно, что 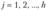 для всех
для всех 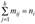 . В результате классификации элементов по h группам мы получим lh чисел, которые представим в табличном виде.
. В результате классификации элементов по h группам мы получим lh чисел, которые представим в табличном виде.
Номер выборки. | Число элементов в группах. | Итого по строкам. | |||
 |  |  |  | ||
 |  |  |  | ||
 |  |  |  | ||
Итого по столбцам. | 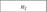 | 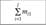 |  |  | |
Здесь  — общее число всех наблюдений по всем выборкам.
— общее число всех наблюдений по всем выборкам.
Требуется проверить гипотезу о том, что вероятность 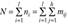 попадания элемента в соответствующую группу оавна для всех совокупностей, т. е. нулевую гипотезу для всех j = 1, 2,…, h.
попадания элемента в соответствующую группу оавна для всех совокупностей, т. е. нулевую гипотезу для всех j = 1, 2,…, h.
Нулевую гипотезу проверяют против конкурирующей гипотезы Я, состоящей в том, что вероятности не равны.
В качестве критерия можно использовать статистику.
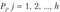
где 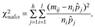 для всех
для всех 
При справедливости нулевой гипотезы Я0 статистика 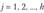 имеет распределение
имеет распределение  степенями свободы.
степенями свободы.
Для проверки нулевой гипотезы на уровне значимости, а строят правостороннюю критическую область, границы которой определяются из условия.
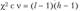
Критерий проверки гипотезы заключается в следующем: если  , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 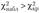 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.
Проверка гипотез о законе распределения генеральной совокупности.
Проверка гипотез о законе распределения значений признака X в генеральной совокупности осуществляется с помощью критериев согласия.
Критерий согласия — статистический критерий, предназначенный для проверки гипотезы //0 о том, что ряд наблюдений 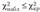 образует случайную выборку, извлеченную из генеральной совокупности X с функцией распределения
образует случайную выборку, извлеченную из генеральной совокупности X с функцией распределения 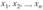 , где общий вид функции F (x) считается известным, а параметры
, где общий вид функции F (x) считается известным, а параметры 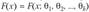 могут быть как известными, так и неизвестными. Критерий согласия основан на использовании различных мер расстояний между анализируемой эмпирической функцией
могут быть как известными, так и неизвестными. Критерий согласия основан на использовании различных мер расстояний между анализируемой эмпирической функцией  распределения, определенной по выборке, и функцией распределения F (x) генеральной совокупности X.
распределения, определенной по выборке, и функцией распределения F (x) генеральной совокупности X.
Математически нулевую гипотезу можно записать в следующем виде:
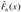
где  — вероятность попадания предполагаемой случайной величины X в г'-й интервал, где i = 1,…, /, или вероятность принятия ею i-ro значения.
— вероятность попадания предполагаемой случайной величины X в г'-й интервал, где i = 1,…, /, или вероятность принятия ею i-ro значения.
Критерий состоит в том, что выбирается некоторая случайная величина (статистика) Т", являющаяся мерой расхождения (рассогласования) между рядом наблюдений и предполагаемым теоретическим распределением.
При проверке нулевой гипотезы заранее задается уровень значимости, а (а = 0,1; 0,05; 0,01). Затем на основании закона распределения Тп находится такое значение 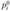 , что
, что 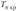
Критическое значение  обычно получают из таблиц соответствующей функции распределения.
обычно получают из таблиц соответствующей функции распределения.
Далее на основании выборки вычисляетсянаблюдаемая величина 
Наконец, сравниваются два значения:  и
и  . Если
. Если 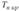 , то нулевая гипотеза отвергается. Если же
, то нулевая гипотеза отвергается. Если же 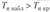 , то нулевая гипотеза не отвергается; в этом случае отклонения от предполагаемого теоретического закона распределения считаются незначимыми, т. е. данные наблюдения не противоречат гипотезе о виде распределения.
, то нулевая гипотеза не отвергается; в этом случае отклонения от предполагаемого теоретического закона распределения считаются незначимыми, т. е. данные наблюдения не противоречат гипотезе о виде распределения.
Случайная величина Т" есть функция наблюдаемых относительных частот, и в зависимости от вида этой функции распределение Т" будет задавать соответствующий критерий согласия.
Критерий согласия Пирсона. Данный критерий (другое название — критерий х2) имеет наибольшее применение. Согласно этому критерию.
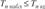
Для расчетов удобно ввести понятие теоретической частоты 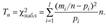 и воспользоваться формулой.
и воспользоваться формулой.

Как известно, распределение 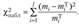 зависит от числа степеней свободы. При применении критерия Пирсона это число находится по формуле v = / - г — 1, где г — число параметров предполагаемого теоретического закона, использованных для вычисления теоретических частот и оцениваемых по выборке.
зависит от числа степеней свободы. При применении критерия Пирсона это число находится по формуле v = / - г — 1, где г — число параметров предполагаемого теоретического закона, использованных для вычисления теоретических частот и оцениваемых по выборке.
Гипотеза отвергается на уровне значимости а, если вычисленное значение Хда6л окажется больше критического x2p (ot, v), найденного по таблицам распределения /2 для уровня значимости, а и числа степеней свободы v = / - г — 1. [5 противном случае гипотеза не отвергается [27, 28].
При расчете Хтбл следует учитывать требование mj >5. Поэтому предварительно рекомендуется объединять соседние интервалы таким образом, чтобы т' > 5 для объединенных интервалов. При этом объем выборки должен быть достаточно велик (я > 50). Расчет х2айл удобно производить в табличном виде.
Варианты или интервалы. | Частоты тп. | Pi | Теоретические частоты mj = npi. |  | 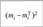 |
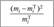 | 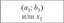 |  | 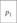 |  |  |
 | 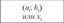 |  |  |  | 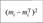 |
 | 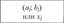 |  |  |  | 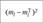 |
 |  |  |  |  |  |
Поясним некоторые моменты вычислений.
В столбце 4 таблицы некоторые соседние частоты могут суммироваться для удовлетворения условия mj >5. Тогда соответствующие соседние интервалы (варианты) объединяются в один интервал <�х<�х^+1у (г) — номер наименьшего, (г + 1) — номер наибольшего из объединяемых соседних вариантов. Расчеты в столбцах 2−6 проводятся для вновь образованного вариационного ряда, причем количество интервалов (вариантов) (/) в новом ряде учитывается при расчете числа степеней свободы.
Теоретические законы, как правило, определяются для всех действительных значений случайной величины. Это обстоятельство следует учитывать при получении вероятностей ph т. е. учитывать, если это необходимо, расширенные интервалы (-; />,) и (а,).
При расчете теоретических частот иногда производят округление до целых чисел, однако при этом должно выполняться равенство 
Критерий Колмогорова. Критерий применяется тогда, когда теоретическое распределение заранее полностью определено (например, известны все значения параметров, определяющие распределение).
Согласно этому критерию.

где 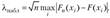 — эмпирическая функция распределения, т. е.
— эмпирическая функция распределения, т. е. 
для интервального ряда с центрами 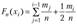 и
и 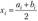 для дискретного ряда;
для дискретного ряда;  — теоретическая функция распределения (интегральная функция).
— теоретическая функция распределения (интегральная функция).
Для вычисления 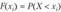 употребляется формула
употребляется формула  , где.
, где.
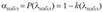
Функция k (X) (или Р (А)) табулирована.