Доказательство теоремы Гаусса—Маркова. 
Оценка дисперсии возмущений

Теперь мы имеем возможность привести доказательство теоремы Гаусса—Маркова, сформулированной в § 4.2.

Выше (§ 4.2) мы уже показали, что оценка метода наименьших квадратов b = (X' Х)~^х Х’У есть несмещенная оценка для вектора параметров р, т. е. М (Ь) = р. Любую другую оценку Ь вектора р без ограничения общности можно представить в виде.

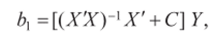
где С — некоторая матрица размера (p+l)x/j.

Так как рассматриваемые в теореме оценки относятся к классу несмещенных оценок, то и М (Ь) = р или М (Ь) = = MW’Xy’X' + Cl Y = р.

Учитывая, что матрица в квадратных скобках — неслучайная, а в силу предпосылки 2 регрессионного анализа Л/(е)=0, получим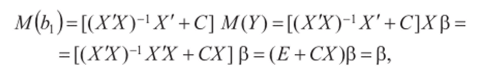

откуда следует, что СХ— 0.

Далее.

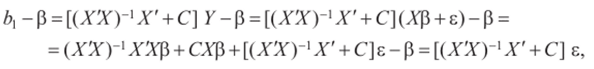
так как СХ= 0, (XX)-'ХХ$ = Е$ = $.

Теперь с помощью преобразований, аналогичных проведенным при получении формул (4.15), (4.16), найдем, что ковариационная матрица вектора оценок Ь, т. е.

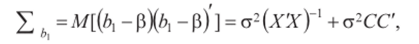
или, учитывая (4.16),.

Диагональные элементы матрицы СС' неотрицательны^[1], ибо они равны суммам квадратов элементов соответствующих строк этой матрицы. А так как диагональные элементы матриц Y и.

Y есть дисперсии компонент векторов оценок Ьц и b_h то дис-

ь

Персия а? >а^ (/=1,2,…, />+1). Это означает, что оценки коэффициентов регрессии, найденных методом наименьших квадратов, обладают наименьшей дисперсией, что и требовалось доказать.

Итак, мы доказали, что оцека b метода наименьших квадратов является «наилучшей» линейной оценкой параметра р. Перейдем теперь к оценке еще одного параметра — дисперсии возмущений а².

Рассмотрим вектор остатков е, равный в соответствии с (4.2') е= Y— ХЬ.

В силу (4.2) и (4.8)

или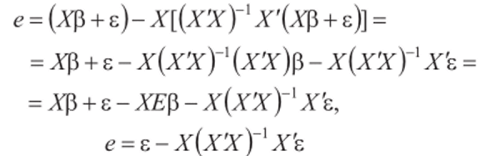

(учли, что произведение (X'Х)~^х(Х'Х)=Е, т. е. равно единичной матрице Е_р+ (р+ 1)-го порядка).

Найдем транспонированный вектор остатков е'. Так как при транспонировании матрица (Х'Х)~^] не меняется, т. е.

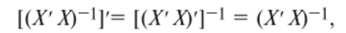
то.

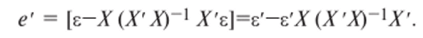
Теперь.

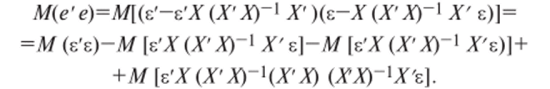
Так как последние два слагаемых взаимно уничтожаются, то.

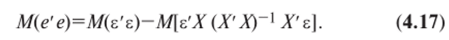
Первое слагаемое выражения (4.17) 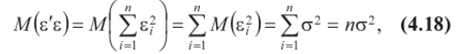ибо в силу предпосылок 2,3 регрессионного анализа.

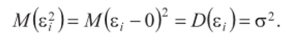
Матрица В =X (X'X)~^l X' симметрическая (§ 13.8), так как.

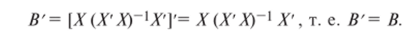
/г.

Поэтому 8'Be представляет квадратическую форму, е_у-;

*v=i.

ее математическое ожидание.

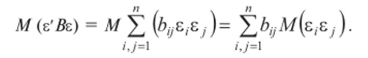
Последнюю сумму можно разбить на две составляющие суммы элементов на главной диагонали матрицы В и вне ее:

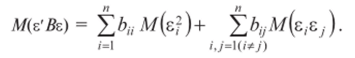
Второе слагаемое равно нулю в силу предпосылки 4 регрессионного анализа, т. е. m (s, s.)= 0. Сумма диагональных элементов матрицы В образует след матрицы tr (?)(§ 13.8). Получим.

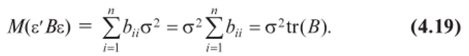
Заменив матрицу В ее выражением, получим.

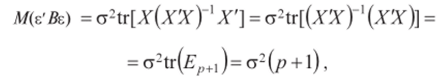
так как след матрицы не меняется при ее транспонировании (см. § 13.14), т. е. tr (y4C)= tr (C4), а след единичной матрицы (т.е. сумма ее диагональных элементов) равен порядку этой матрицы. Теперь по формуле (4.17), учитывая (4.18) и (4.19), получим: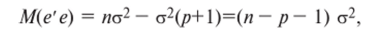

т. е.

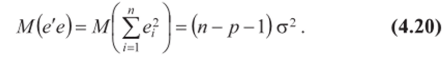
Равенство (4.20) означает, что несмещенная оценка s² параметра а² или выборочная остаточная дисперсия s² определяется по формуле:

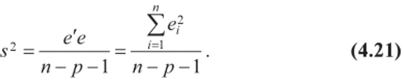
Полученная формула легко объяснима. В знаменателе выражения (4.21) стоит п — (р+), а не п—2, как это было выше в (3.26). Это связано с тем, что теперь (р+1) степеней свободы (а не две) теряются при определении неизвестных параметров, число которых вместе со свободным членом равно (/?+1).

Можно показать, что рассмотренные в этом параграфе оценки b и s¹ параметров р и а² при выполнении предпосылки 5 регрессионного анализа о нормальном распределении вектора возмущений е (е ~ N_n (0;а²?")) являются независимыми. Для этого в данном случае достаточно убедиться в некоррелированности оценок b и s².

• [1] Матрица СС' гак же, как и ковариационные матрицы Y ^ и Y «явяяетсянеотрицательно определенной (см. § 13.8). В этом смысле можно записать, чтоматрица V >У. , т.с. вектор оценок b = (Л» Х)~]Х' У, полученный методом Ь 1-~‘ п наименьших квадратов, обладает меньшим рассеиванием относительно параметра р по сравнению с любым другим вектором несмещенных оценок.