Основы финансовых вычислений

Определить размер наращенной суммы для различных способов расчета по простой годовой ставке ссудных процентов. Год не високосный. Сделать выводы.

Дано:

P = 100 млн руб.

r = 12,5%.

tвыд. = 8,03.

tвоз. = 15,12.

K = 360 дней.

• ? = 272 дня
• S — ?

Решение: Способ расчета процентов: французская практика.

Для этого пользуемся формулой.

S = P*(1+T/K*r).

S= 100 000 000*(1+272/360*0,125)=109 444 444 руб.

Вывод: При вкладе под германскую практику под 12,5% год 100 млн руб. получим сумму равную 109 444 444 руб.

Задача № 2.

RaiffeisenBANK предлагает компании ЗАО «Совтрансавто» разместить свободные денежные средства в сумме 5 млн руб. на его депозитных счетах с плавающей процентной ставкой сроком на один год. Процентный доход выплачивается ежемесячно — первые полгода по ставке 14% годовых, затем с увеличением доходности на 1,0% на каждые последующие 2 месяца. Составить график платежей по данному банковскому депозиту. Представить его в таблице. Вычислить сумму платежей. Сделать вывод.

Дано:

Р=5 млн. р

R1=14%.

R2=15%.

R3=16%.

R4=17%.

Найти S1,2,3,4.

Решение:

S = P*(1+(tn-t0)*r).

S1=5*(1+0,14*0,5)=5,35 млн. р

S2=5,35*(1+0,15*2/12) = 5,5 млн. р

S3=5,5*(1+0,16*2/12) =5,65 млн. р

S4=5,65*(1+0,17*2/12) = 5,81 млн. р процент начисление банковский депозит.

График 1. Изменение наращенной суммы в зависимости от плавающей процентной ставки.

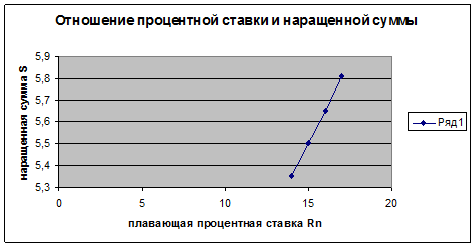
Таблица 1. Платежи по банковскому депозиту.

Вывод: Чем больше процентная ставка и чем чаше она начисляется, тем больше наращенная сумма.

Задача № 3.

Рассчитать наращенную сумму с исходной суммы в Р=8,5 млн руб. при размещении ее в банке на условиях начисления простых и сложных процентов, если: а) годовая ставка 17%, б) периоды наращения: 30 дней, 90 дней, 180 дней, 1 год, 5 лет, 10 лет. Год принять равным 360 дням. Представьте графически изменения наращенной суммы в зависимости от схемы начисления процентов (простая или сложная) и периода наращения процентов. Сделайте выводы по каждому пункту задачи.

Решение:

Начисление простых процентов происходит по формуле.

S1, пр. = P*(1+n*r).

Начисление сложных процентов происходит по формуле.

S1, сл. = P*(1+r)n.

Результаты расчетов представим в виде таблицы.

Таблица 1. Изменение наращенной суммы в зависимости от схемы начисления процентов.

График 1. Изменение наращенной суммы в зависимости от схемы начисления ссудных процентов.

Вывод: При начислении процентов в период менее одного года максимально выгодным является начисление простых ссудных процентов;

При начислении процентов в период более одного года максимальную наращенную сумму можно получить при начислении сложных ссудных процентов;

При начислении процентов сроком в 1 год, наращенная сумма по простым и сложным процентам будет одинакова.

Задача 4.

Пенсионер положил 12 000 руб на срочный пенсионный вклад на 5,5 лет под 12,5% годовых с начислением процентов 12 раз в год. Какая сумма у него накопится в конце срока, и какой процент он сможет снять? Каков коэффициент наращения?

Дано:

P=120 000 руб.

N=5,5 лет.

R=12,5%.

M=12.

Решение:

Для определения суммы, которую можно будет получить при предоставленных условиях, используют формулу.

S=P*(1+r/m)^n*m.

S=120 000*(1+0,125/12)^5,5*12=237 801 руб.

Кн=S/P=237 801/120000=1,98.

Вывод: по истечении срока у пенсионера накопится сумма в размере 237 801 руб. Коэффициент наращения равен 1.98, вложенная сумма увеличится на 98%.

Задача 5.

От продажи родительского дома у Вас оказалось P тыс.руб.Вы знаете, что в течение n лет Вам эти деньги не понадобятся. Вы решили открыть счет в банке при том, что годовая ставка r %. Банк предлагает следующие виды вкладов:

• 1)ежемесячное начисление процентов.
• 2)ежеквартальное начисление процентов
• 3)депозит на 6 месяцев
• 4)депозит на 12 месяцев.

Какой из вкладов принесет больший доход через n лет? Обосновать ответ.

Дано:

P=120 000 руб.

N=4 лет.

R=12,5%.

Решение:

Для определения суммы, которую можно будет получить при предоставленных условиях, используют формулу S=P*(1+r/m)^n*m.

При подстановке данных в формулы получим результаты для всех 4 случаев.

• 1)S=120 000*(1+0,125/12)^4*12=197 336 руб.
• 2)S=120 000*(1+0,125/4)^4*4=196 338 руб.
• 3)S=120 000*(1+0,125/2)^4*2=194 900 руб.
• 4)S=120 000*(1+0,125)^4=192 217 руб.

Вывод: Из предоставленных данных можно сделать вывод, что если вкладывать 120 000 руб. под сложный процент на 4 года, то наибольшую выгоду можно будет получить при ежемесячном начислении процентов. Из этого вытекает свойство: чем большее количество раз начисляется процент в год, тем больше полученная сумма S. В данном случае наибольшая наращенная сумма получилась при ежемесячном начислении процентов равная 1 500 944 руб.

Задача 6.

Сколько лет нужно копит деньги при первоначальном взносе P руб. годовой процентной ставке r % и ежеквартальных начислениях, чтобы накопить S руб.

Дано :

P=5000 руб.

S=10 000 руб.

r=8%.

m=4.

Решение:

Для расчета количества лет пролoгарифмируем формулу.

S= P*(1+r/m)^n*m.

и выразим n. Получим.

n=(ln (S/P)/(ln (1+r/m)*m).

При подстановке значений получим.

n=(ln (10 000/5000)/(ln (1+0,08/4)*4)=9 лет.

Вывод: Для того чтобы при первоначальном капитале 5000 руб. получить 10 000 руб. следует вложить первоначальную сумму в банк на 9 лет с ежеквартальным начислением процентов, и годовой процентной ставке равной 8%.