Актуализация личного опыта учащихся

В профессиональной математической деятельности обычно имеет место баланс интуитивных и логических компонентов опыта. Более того, судя по мемуарным источникам, основная идея и суть метода, как правило, интуитивно постигаются математиками задолго до того, как они находят рациональное (логическое) обоснование и оформление. По мнению М. Клайна, «великих математиков всегда отличала тонкая интуиция, позволявшая им избегать катастрофических ошибок» (Клайн, 1984, с. 195). При этом под интуицией Клайн понимал «…не веру в шаткое свидетельство чувств и не обманчивое суждение беспорядочного воображения, но понятие ясного и отчетливого ума, настолько простое и очевидное, что оно не оставляет никакого сомнения в том, что мы мыслим» (там же, с. 196). Нет никаких оснований полагать, что учебная математическая деятельность устроена принципиально иначе: разве что математик делает за свою жизнь небольшое число объективно новых открытий, тогда как школьник за десять лет обучения в школе — великое множество субъективно новых открытий, повторяя непростой путь всей истории математики.

Таким образом, одним из важнейших аспектов проблемы организации учебного текста является вопрос о соотношении интуиции и логики в изложении материала. Для этого, однако, нужно доверять личному опыту учащихся и создавать условия для его актуализации.

Одним из средств актуализации личного опыта школьников являются дидактические игры. В работах В. М. Букатова, В. В. Волиной, Л. С. Выготского, Е. А. Дышинского, Т. К. Жигалкиной, В. Г. Коваленко, Е. М. Минскина, В. А. Трайнева, С. А. Шмакова, Д. Б. Эльконина и др. рассматриваются функции игры, в том числе дидактической игры, особенности ее организации.

Д. Б. Эльконин отмечает значение игры для преодоления познавательного эгоцентризма, формирования умственных действий, развития произвольного поведения (Эльконин, 1999). Исследования С. А. Шмакова, Е. М. Минскина, В. М. Букатова показывают роль игры в развитии у учащихся кругозора, воображения, фантазии, уверенности в себе. Игра помогает учащимся лучше узнать свои учебные возможности, проявить себя как организатора учебной деятельности, научиться работать в коллективе, продемонстрировать необычность, виртуозность своего мышления.

С. А. Шмаков выделяет четыре черты, присущие играм: свободная развивающая деятельность; творческий, в значительной мере импровизированный, активный характер этой деятельности, ее эмоциональная приподнятость; соперничество, сосредоточенность, конкуренция; наличие прямых или косвенных правил, отражающих содержание игры, логическую и временную последовательности ее развития (Шмаков, 2003).

В учебных книгах «обогащающей модели» представлены тексты, которые предлагают учащимся сюжетные, ролевые, имитационные игры, игры-драматизации. Назовем такой тип текстов «текст — игра».

Так, в итоге изучения различных тем школьного курса мы предлагаем учащимся организовать интеллектуальные игры, такие как «Праздник знаний», «Бал», «Ярмарка», «Аукцион» и т. д. При конструировании этих текстов важным является представление игрового условия — правила, при этом оно не должно быть похоже на постановку учебной задачи.

Критикуя организацию дидактических игр в школе, В. М. Букатов справедливо отмечает: «Правила, которые в подлинных детских играх всегда нагнетают какую-то тайну (хотя бы — кто победит?), а потому гармонично сопрягаются с субъектностью, после учительских объяснений оказываются всего лишь образовательными целями» (Букатов, 2003, с. 83).

Как показывают исследования, введения в тексты — игры должны быть такими, чтобы они носили проектный характер, приглашали школьников к сотрудничеству, задавали эмоциональный тон предстоящей деятельности. Приведем фрагмент из введения к тексту «Праздник знаний» (тема «Положительные и отрицательные числа», 6-й класс).

Праздник знаний

Работа над книгой подошла к концу. Пора подводить итоги. Можно по этому поводу устроить праздник — праздник знаний, пригласить на праздник приятелей, придумать игры, забавы, подобрать интересные задачи, устроить конкурсы, приготовить угощение.

Входной билет на праздник может выглядеть, например, так:

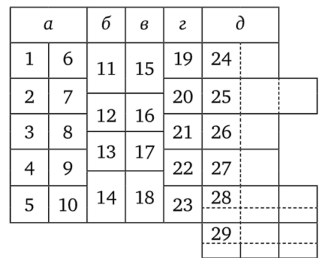
Чтобы войти в праздничный зал, нужно правильно ответить на 10 вопросов и заполнить первые 10 клеток на билете…

(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005, с. 22А— 227.).

Мы предлагаем учащимся игры, включающие не только те задания, которые в какой-то степени известны учащимся, но и задания, входящие в «зону их ближайшего развития». Это дает возможность школьникам проявить свою индивидуальность, в том числе и свою интуицию. Так, итогом работы по теме «Тождества сокращенного умножения» (7-й класс) является игра «Аукцион». Соответствующий макротекст состоит из следующих частей: вступление (раскрываются сюжет игры, роли участников, предполагаемые действия, игровое правило), основная часть (предлагается материал для проведения игры — «алгебраический банк»), заключение (предложения о том, как можно неформально подвести итоги аукциона, список книг, которые могут помочь в подборе заданий в алгебраический банк). Приведем фрагмент из вступления к данной игре.

Приглашаем на аукцион тождеств сокращенного умножения

Условия аукциона

На торг выставляются формулы, получаемые из тождеств сокращенного умножения.

Плата должна быть особой. Каждая задача, для решения которой применяется объявленная к продаже формула, оценивается в баллах. Эти баллы и будут «деньгами» на нашем аукционе.

Стартовая цена одного лота, т. е. одной формулы, — 5 баллов. Поэтому прежде чем участвовать в аукционе, следует запастись решениями задач из алгебраического банка. Задачи, придуманные вами и пополняющие этот банк, оцениваются дороже.

(Тождества сокращенного умножения, 2004, с. 144.).

Как показывает практика, во время этой игры и учитель, и школьники стараются сохранить атмосферу аукциона, выбрав либо форму работы в группах, либо определяя личное первенство.

Особое место среди текстов типа текст — игра занимают ролевые игры, в которых учащимся предлагается выступить в роли «рецензента», «учителя», «алгебраиста», «экспериментатора», «разработчика средств контроля» и т. д.

Остановимся еще на одной особенности текстов — игр. Они должны, на наш взгляд, предполагать соавторство, участие школьников в их усовершенствовании, развитии. Приведем фрагмент текста для школьников 6-го класса (тема «Положительные и отрицательные числа»), в котором им предлагается проявить инициативу при участии в празднике знаний по итогам изучения данной темы.

Любимое занятие

Вам потребуется шесть комнат (или шесть столов в праздничном зале), в каждой из которых вы можете устроить игры. Пусть ваши гости выберут комнату на свой вкус, только попасть в желанную комнату можно будет, поставив в табличке на двери вместо звездочки нужный знак («+» или «—»), а вместо «…» — нужное положительное число.

Таблички могут выглядеть так:

Заметим, что в двух последних примерах возможны два варианта решения.

Придумайте игры для каждого зала и играйте со всеми желающими…

(Математика-5. Ч. 2. Положительные и отрицательные числа, 2005,.

с. 226—227.).

Иногда приходится слышать, что строить все обучение на интересе нельзя, так как школьники могут привыкнуть делать только то, что интересно, и не станут выполнять работу не очень интересную, но необходимую. Мы считаем, что наличие интереса, стимулированного содержанием математической деятельности, не только является условием понимания учебного материала, но и создает в классе особую рабочую атмосферу сотрудничества.

Еще одним из приемов привлечения личного опыта учащихся в обучении является использование текстов, которые можно назвать «текст — метафора». Обычно понятие метафоры определяют следующим образом: метафора (греч. metaphora — перенос) — это фигура речи (в виде слова или словосочетаний), обозначающая некоторый объект или класс объектов для характеристики другого, сходного с данным объектом или классом объектов.

Понятие метафоры изучается представителями разных областей знаний: философии, психологии, герменевтики, семиотики, дидактики. Выделены важные функции метафоры как особого средства познания (Арутюнова, 1990; Бачков, 2004; Крюкова, 2000; Новикова, 2004 и др.):

• 1) объединение рационального и эмоционально-ценностного опыта личности в процессе познания;
• 2) усиление эмоциональной окраски содержания понятия (метафора выступает в виде «приятного интеллектуального сюрприза»);
• 3) облегчение понимания за счет привлечения внимания к некоторому ключевому признаку объекта («у этой женщины острый язык»);
• 4) появление скрытых смыслов на основе разрыва привычных содержательных связей, возможность увидеть новое содержание («архитектура — это застывшая музыка»);
• 5) одномоментное схватывание сути («между пальцами года протекают без следа, протекают как вода — кап, кап…»);
• 6) пробуждение творческих ресурсов воображения за счет эффекта необычности, неожиданности;
• 7) актуализация архетипического опыта (с этой точки зрения сказка — это своего рода метафора по отношению к базовым формам житейского опыта);
• 8) коммуникативное звено, облегчающее взаимопонимание между людьми;
• 9) метафора лаконична, она сокращает речь, устанавливает устойчивое подобие, обусловливает ассоциативное обращение к вещам и явлениям обыденного мира.

Н. Малара и Дж. Наварра раскрывают роль метафоры как «дидактического посредника» в обучении математике. Они отмечают, что метафора оказывает помощь в изучении трудных тем: «весы» — в изучении теории преобразований уравнений, «бусы» — в изучении свойств последовательностей, «пирамиды» — при изучении операции над числами и т. д. (Malara, Navarra, 2003).

Приведем примеры текстов в учебных книгах «обогащающей модели» обучения, которые можно отнести к типу «текст — метафора».

Обычно учащиеся испытывают затруднения при преобразовании алгебраических выражений. Одной из причин этого является то, что они не осознают («не принимают») цели предстоящей, иногда трудоемкой работы. В начале изучения тождественных преобразований с помощью разложения многочленов на множители мы используем метафору «превратить „слона“ в „муху“», что дает школьникам возможность одним взглядом охватить суть предстоящей деятельности. Приведем фрагмент этого текста («Тождества сокращенного умножения», 7-й класс).

Представьте, что вам предложили найти значение многочлена.

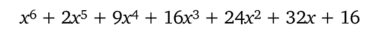
при х = 2 или при х = -13 821. Или вас попросили ответить на вопрос, каким — положительным, отрицательным или нулем — окажется значение этого многочлена прих = -13 821.

Вы уже, наверное, понимаете, что непосредственное вычисление займет у вас слишком много времени. Понравится ли вам идея разложения многочлена на множители? Идея, которая позволит превратить данного вам «слона» в «муху» и получить такое равенство:

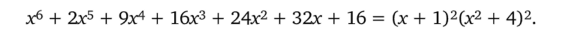
Неплохо, верно?

Давайте проследим, как получить такое равенство, и выясним, является ли оно тождеством…

(Тождества сокращенного умножения, 2004, с. 117.).

При изучении тождеств сокращенного умножения мы используем метафору «снять маску» для опознания учащимися выражений, которые могут быть преобразованы с помощью той или иной формулы. Приведем фрагмент текста, настраивающего учащихся на использование этого приема.

Если внимательно присмотреться к выражению (—а — Ь)², то в нем можно увидеть левую часть нашей знакомой формулы:

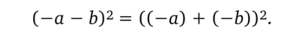
Формула как будто бы надела на себя маску, а мы эту маску сняли.

(Тождества сокращенного умножения, 2004, с. 10—11.).

Эта метафора в дальнейшем помогает учащимся выделить этап «снять маску» в процессе работы с алгебраическими выражениями.

Рассмотрим еще один пример использования метафоры. Для понимания природы иррационального числа важен тот факт, что каждой бесконечной десятичной дроби соответствует единственная точка на числовой оси, и наоборот, любой точке числовой оси соответствует единственная бесконечная десятичная дробь. Однако для учащихся этот факт далеко не очевиден. В качестве метафоры, позволяющей раскрыть сущность иррационального числа, предлагается текст, иллюстрирующий деятельность фантастического автомата. Приведем его фрагмент (тема «Действительные числа. Иррациональные выражения», 8-й класс).

Возьмем, например, бесконечную непериодическую дробь.

15,123 456 789 101 112…,.

где после запятой в ее записи одно за другим идут числа натурального ряда.

Как изобразить эту дробь? Как найти ее место на числовой оси? Обратимся за помощью к «технике». Представим, что у нас есть автомат, который может выполнять процедуры:

• 1) последовательно считывать цифры в записи десятичной дроби;
• 2) строить отрезок единичной длины;
• 3) делить любой отрезок на десять равных частей;
• 4) выбирать некоторый отрезок из числа построенных.

Такой автомат каждой бесконечной непериодической дроби может поставить в соответствие единственную точку числовой оси.

Работа автомата с дробью 15,123 456 789 101 112… идет по следующим шагам…

(Действительные числа. Иррациональные выражения, 2004, с. 49—50.).

По нашему замыслу, эта метафора «автомата» должна сыграть эвристическую функцию в изучении учащимися действительных чисел. М. Минский рассматривает связь метафоры и фрейма (особой разновидности когнитивной схемы), подчеркивая, что метафоры образуют непредсказуемые межфреймовые связи большой эвристической силы, обеспечивающие концептуализацию определенного фрагмента действительности по аналогии с уже сложившимися системами понятий (Минский, 1978).

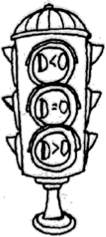
Соответственно в учебные книги включены тексты, которые позволяют с помощью метафоры схематично закрепить неизменные и меняющиеся свойства изучаемого понятия или явления. Так, одним из свойств квадратного уравнения является наличие или отсутствие у него корней в зависимости от значения выражения D = Ъ² — 4ас. Чтобы этот факт принял форму когнитивной схемы, учащимся предлагается текст, включающий метафору (тема «Квадратные уравнения», 8-й класс):

Дискриминант обозначается буквой D:

Попробуйте установить связь между понятиями «светофор» и «дискриминант». Приведите примеры таких ситуаций, в которых удобно использовать «устройства», аналогичные дискриминанту.

(Квадратные уравнения, 2002, с. 45.).

Отмечая эвристическую роль метафоры в математической деятельности, Д. Пойа пишет; «Достаточно часто отмечалось, что язык, которым мы пользуемся, полон метафор (слабых, посредственных и ярких). Однако мне не известно, замечено ли также то, что многие из этих метафор взаимозависимы: они могут быть как-то связаны между собой, как-то объединены, могут образовывать более или менее независимые или, наоборот, более или менее сцепленные между собой группы» (Пойа, 1970, с. 184).

Как эвристический прием для организации поиска решения задачи сконструирован текст, который оформлен в виде анкеты, включающей вопросы, на которые полезно отвечать, решая задачу. Работая с этим текстом — метафорой, школьники получают соответствующую когнитивную схему-процедуру решения текстовых задач. Приведем пример этой анкеты.

Анкета

• 1. Какой процесс рассматривается в задаче:
  • а) движение;
  • б) выполнение работы;
  • в) покупка товара;
  • г) измерение площади;
  • д) другой процесс?
• 2. Какие величины необходимы для описания процесса:
  • а) скорость движения (v); время движения (t); пройденное расстояние (s);
  • б) производительность труда (АО; время, потраченное на работу (t); объем

выполненной работы (А);

в) цена товара (р); количество приобретенного товара (п); общая сумма, потраченная на приобретение товара (с);

• г) длина участка (а); ширина участка (Ь); площадь участка (5);
• д) другие величины?
• 3. Каковы связи между величинами:
  • а) s = v • t;
  • б) А = N? t;
  • в) С = р? п)
  • г) S = а • Ь;
  • д) другая связь?
• 4. Какой способ наглядного представления условий задачи вы выбрали:
  • а) табличный;
  • б) рисунком;
  • в) графический?
  • (Квадратные уравнения, 2002, с. 122—123.)

Метафора может приобретать форму макротекста, участвуя в объяснении сложного процесса и помогая образно раскрыть сложную проблему. Например, с помощью метафоры «Планета Кварта» и «Планета Квинта», на которых действуют свои правила выполнения действий над числами, учащиеся знакомятся с важнейшими понятиями алгебры (тема «Алгебраические дроби», 7-й класс).

С нашей точки зрения, разработка текстов — метафор и их включение в школьный учебник является перспективным направлением методики преподавания математики. Неожиданность, непредсказуемость, оригинальность метафоры позволяют выходить за пределы привычных представлений, развивать интуицию и, главное, апеллировать к личному опыту ученика.