Гипотетический диалог Фишера, Хайска, Кейнса и Фридмана по поводу теорий экономических циклов

Рассмотрим динамическую систему, заданную дифференциальным уравнением.

где теК", а отображение / :К" —"R" обладает всеми свойствами, необходимыми для того чтобы решение этого уравнения существовало для достаточно обширного множества начальных состояний. Точкой над х обозначается производная по времени.

Точка х называется состоянием равновесия, если /(х) = 0, т. е. если x (t)-x, о), является решением уравнения (А.1). Состояние равновесия х называется (локально) асимптотически устойчивым, если для всех начальных значений, лежащих в некоторой окрестности точки х, динамическая система сходится к х (иначе говоря, 35 > 0, такое, что из ||л'₀ -х||<8 вытекает, что решение x (t) уравнения (А.1) с начальным условием х (0) = х₀ сходится к х при t—>°°). Если такая сходимость имеет место для любого начального х₀, то х называется глобально асимптотически устойчивым.

Рассмотрим сначала простейший одномерный случай (п = 1), предполагая, что функция /задана на некотором интервале (а, Ь) и удовлетворяет на этом интервале стандартным условиям теорем существования и единственности решения. Предположим, кроме того, что на интервале (а, Ь) имеется единственное решение х уравнения /(х) = 0, причем а<�х <�х => /(х)>0; х<�х /(х)< 0.

Предложение А.1. Пусть x (t) — решение рассматриваемого уравнения

для х (0) е (й, Ь). Тогда x (t) —> х, т. е. состояние равновесия х является гло-

г-«°°.

больно асимптотически устойчивым.

Некоторым аналогом этого утверждения в дискретном времени служит следующее предложение.

Предложение А.2. Пусть на интервале (а, b) заданы две непрерывные монотонно возрастающие функции ф (.г) и ф (х). Пусть, далее, уравнение ср (х) = |/(.г) имеет на (а, Ь) единственное решение х, причем й<�хф (х)>|/(х); х<�х<�Ь=$ ф (х) < ф (х). Тогда любая последовательность (х,)_/=01 постро

енная по правилу

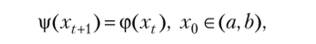
сходится к х.

Заметим, что условие монотонности функций ф (х) и V|/(x) является в дискретном случае существенным, хотя его и можно в значительной мере ослабить.

где А — линейное отображение, которое мы будем отождествлять с его матрицей в естественном базисе. Уравнение имеет по крайней мере одно состояние равновесия, а именно х = 0. Состояние равновесия х = 0 системы (А.2) глобально асимптотически устойчиво тогда и только тогда, когда вещественные части всех собственных чисел матрицы, А отрицательны.

Утверждение А.2. Рассмотрим систему (А.1) в общем виде. Пусть х — ее состояние равновесия. Мы предполагаем, что функция / непрерывно дифференцируема. Обозначим через А (х) матрицу частных производных отображения / в точке х. Для локальной асимптотической устойчивости состояния равновесия достаточно, чтобы вещественные части всех собственных чисел матрицы А (х) были отрицательны.

Напомним, что число А. называется собственным числом матрицы А, если Ах = Хх для некоторого х ^ 0, или, иначе, если это число является решением уравнения А-1=0, где I — единичная матрица. В двумерном случае, т. е. при п = 2, проверить (локальную) асимптотическую устойчивость равновесия относительно просто, так как можно заметить, что вещественные.

(^{а a}12l.

части всех собственных чисел матрицы А = отрицательны тогда.

a₂i ^а22)

и только тогда, когда ее след отрицателен, а определитель положителен. Иными словами, должно выполняться +а₂₂ <0 и а_па₂2 ~а2^а2 >0- Двумерный случай удобен еще и тем, что условия глобальной асимптотической устойчивости являются непосредственным обобщением условий локальной асимптотической устойчивости. А именно, имеет место следующее предложение.

Предложение А.З. Рассмотрим систему (А.1) в предположении, что п — 2. Для глобальной асимптотической устойчивости состояния равновесия х достаточно, чтобы для всех х вещественные части всех собственных чисел матрицы А (х) были отрицательными, т. е. чтобы выполнялись

з/, э/₂ _ э/, э/₂ а/, э/₂ _ э/, э/₂ _.

неравенства -^+—^-0, а кроме того, ¹⁰ или

ОХ] Эх₂ ОХ] Эх₂ Эх₂ Эх, Эх, Эх₂

Эх₂ Эх,.