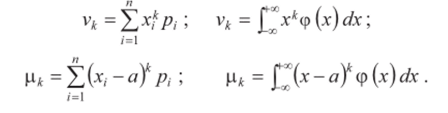Функция распределения случайной величины. 
Непрерывные случайные величины

Функцией распределения случайной величины X называется функция F (x), выражающая для каждого х вероятность того, что случайная величина X примет значение, меньшее х

? Пример 2.5. Дан ряд распределения случайной величины.

Найти и изобразить графически ее функцию распределения. Решение. В соответствии с определением.

F (jc) = 0 при х < 1; F (jc) = 0,4 при 1 < х < 4;

F (x) = 0,4 + 0,1 = 0,5 при 4 < д; < 5; F{x) = 0,5 + 0,5 = 1 при х > 5.

Итак (см. рис. 2.1):

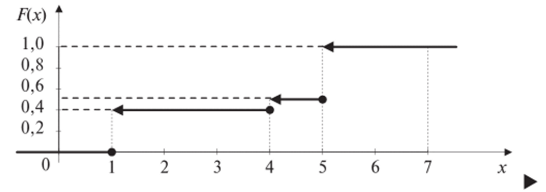
Рис. 2.1.

Свойства функции распределения:

1. Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: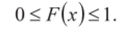

2. Функция распределения случайной величины есть неубывающая функция на всей числовой оси, т. е. при х₂>х

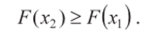
3. На минус бесконечности функция распределения равна нулю, на плюс бесконечности — равна единице, т. е.

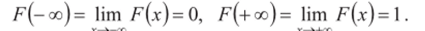
4. Вероятность попадания случайной величины X в интервал [x, x₂) (включая х) равна приращению ее функции распределения на этом интервале, т. е.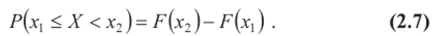

? Пример 2.6. Функция распределения случайной величины X имеет вид:

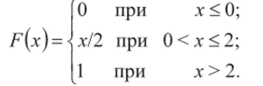
Найти вероятность того, что случайная величина X примет значение в интервале [ 1 ;3).

Решение. По формуле (2.7).

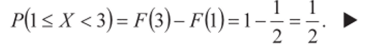
Случайная величина X называется непрерывной, если ее функция распределения непрерывна в любой точке и дифференцируема всюду, кроме, быть может, отдельных точек.

Для непрерывной случайной величины X вероятность любого отдельно взятого значения равна нулю, т. е. Р (Х = q)=0, а вероятность попадания X в интервал (q, Х2) не зависит от того, является ли этот интервал открытым или закрытым (т.е., например, Р (х₁ < X <�х₂ ) = P{_Xl2)).

Плотностью вероятности (плотностью распределения или просто плотностью) <�р (*) непрерывной случайной величины X называется производная ее функции распределения

Плотность вероятности ф (х), как и функция распределения F (x), является одной из форм закона распределения, но в отличие от функции распределения она существует только для непрерывных случайных величин.

Г рафик плотности вероятности называется кривой распределения.

? Пример 2.7. По данным примера 2.6 найти плотность вероятности случайной величины X.

Решение. Плотность вероятности ф (jc) = F'(x), т. е.

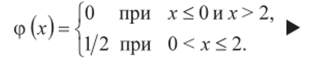
Свойства плотности вероятности непрерывной случайной величины:

1. Плотность вероятности — неотрицательная функция, т. е. ф (х)> 0.

2. Вероятность попадания непрерывной случайной величины в интервал [a, b] равна определенному интегралу от ее плотности вероятности в пределах от а до b (см. рис. 2.2), т. е.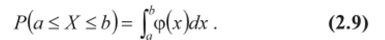

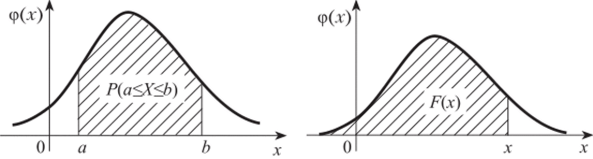
Рис. 2.2 Рис. 2.3.

3. Функция распределения непрерывной случайной величины (см. рис. 2.3) может быть выражена через плотность вероятности по формуле:

F (x)= Jp (*)</*. (2.10).

4. Несобственный интеграл в бесконечных пределах от плотности вероятности непрерывной случайной величины равен единице:

Геометрически свойства / и 4 плотности вероятности означают, что ее график — кривая распределения — лежит не ниже оси абсцисс, и полная площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице.

Для непрерывной случайной величины X математическое ожидание М (Х) и дисперсия D (X) определяются по формулам:

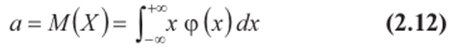
(если интеграл абсолютно сходится); или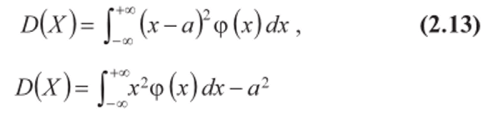

(если приведенные интегралы сходятся).

Наряду с отмеченными выше числовыми характеристиками для описания случайной величины используется понятие квантилей и процентных точек.

Квантилем уровня q (или q-квантилем) называется такое значение x_q случайной величины, при котором функция ее распределения принимает значение, равное q, т. е.

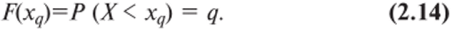
• 100q%-ou точкой называется квантиль X~_q.
• ? Пример 2.8.

По данным примера 2.6 найти квантиль xqj и 30%-ную точку случайной величины X.

Решение. По определению (2.16) F (xo_t3)= 0,3, т. е.

X

~Y~ = 0,3, откуда квантиль х_{0 3} = 0,6. 30%-ная точка случайной величины X, или квантиль Х)_о, з ⁼ xoj" находится аналогично из уравнения ^ = 0,7. откуда *,= 1,4. ?

Среди числовых характеристик случайной величины выделяют начальные v* и центральные р* моменты к-го порядка, определяемые для дискретных и непрерывных случайных величин по формулам: