Первообразные корни и индексы

Пусть (а, т) = 1, тогда а — элемент группы Z_m* порядка ф(т). Порядок элемента а в группе Z_m* (обозначение ordtf (modwz)) есть наименьшее натуральное 5, при котором а^ъ= l (modm). В ряде источников [13, 611 в таком случае пишут, что а принадлежит показателю 5 но модулю т. Если ordtf (modm) = 8, то (а) — циклическая подгруппа порядка 8 группы Z_rn*, отсюда 8|ф (/тг). Если (а) = Z,"*, т. е. ordtf (modm) = ф (т), то а называют первообразным корнем по модулю т. Например, 3 есть первообразный корень по модулю 4.

Утверждение 5.6.

• а) если ordtf (modm) = 8, то а¹ = a^k(modm) / = &(mod8);
• б) если orda (modm) = е8, то orde (modm) = 8;
• в) если orda (modm) = 8 и ordi (modm) = е, то ordab (modm) = НОК (е, 8).

А а) разделим / и к на 8 с остатками: / = 8г/ + г, к — 8? + 5, где г, s < 8. Тогда.

а¹ = а^к а^{Ъ (}1^+г = a^8t+s а' = a^s г = 5, так как элементы 1 = а°> я¹, …, а⁸⁻¹ группы (а) попарно различны.

б) и в) вытекают соответственно из следствия 1 из теоремы 4.10 и теоремы 4.8. ?

Теорема 5.12. Существуют первообразные корни по простому модулю.

р> 2.

Ч Пусть 8j, …, 8,. — различные порядки подгрупп (1), (2), …, (р — 1) группы Z* порядка р — 1, положим п = НОК (8₁,…, 8,.). Поскольку 8_УI (р — 1), i = 1,…, г, то п | (р — 1).

Вместе с тем, 8, I п при i = 1,…, г, поэтому все числа 1, 2,…, (р — 1) е Z_p* суть решения сравнения х^п = l (modp), и эти числа образуют приведенную систему вычетов, т. е. попарно несравнимы по модулю р. Число решений этого сравнения не превышает степени п по теореме 5.86, т. е. р- <�п. Следовательно, п = р — 1. Осталось указать в Z_f)* элемент г порядка п> который и является первообразным корнем по модулю р > 2.

В соответствии с каноническим разложением (2.1) числа п примариый.

к

делитель р-^} делит, по меньшей мере, одно из чисел 8_1? …, 8,., j = 1, …, 5,.

k-

поэтому 8,^ = ар' при некотором t (j) е {1, г). Если ord. r_;(mod/;) = 5,_(;),.

то ord ((x_y)")(modp) = pj по утверждению 5.66. Тогда, положив y_f = (xj)^a, j = 1,5, получаем по утверждению 5.6 В ord2(mod/j) = п, где 2 = y…y_s.? Гаусс доказал: при простом р > 2 имеются первообразные корни по модулю р^к и 2/А где к > 1.

Теорема 5.13. Пусть g — первообразный корень по простому модулю р > 2. Тогда найдется t такое, что на р не делится число и, определяемое равенством.

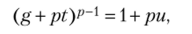
и при таком t число g + pt — первообразный корень по модулю р^к, где k > 1. Л Из малой теоремы Ферма следует, что gp^_1 = 1 + pt₀, тогда.

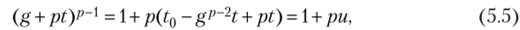
где и одновременно с t пробегает полную систему вычетов по модулю р, поэтому можно указать t такое, что и не делится на р. При данном из (5.5) следует:

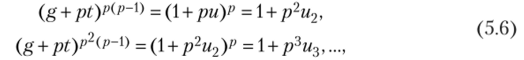
где и₂, м₃,… не делятся на р. Пусть ord (g' + pt)(modp^k) = 5, тогда.

Отсюда (g + pty= l (modp), значит, 5 кратно р — 1. Поскольку 8|ф (/А), где ср(р^к) = р^к~^{(р — 1), то 8 =р^гЛ{р — 1) при некотором re {1…к). Заменив левую часть сравнения (5.7) подходящим (в соответствии с 8) равенством из (5.5) или из системы (5.6), получим при и-и_гг-к, Ъ- ф(р^к), что 1 -г p’u_r — l (mod/j*), р' = 0(modp*). Значит, g + pt — первообразный корень, но mod/A ?

Следствие. Если g, — первообразный корень по модулю р^к при к > 1, то нечетное из чисел g‘₍ и g, + р^к есть первообразный корень по модулю 2/А Л Заметим, что ф (//) = ф (2//^;), и любое нечетное число х удовлетворяет обоим сравнениям: х''= 1(тобр⁴) и/ = l (mod2p^A). Поэтому любое нечетное число х есть первообразный корень по обоим модулям, при этом одно из чисел g₁ и g (+ р^к нечетное. ?

Лемма 5.2. orda (mod2^f) 12^f₂ для любого й е Z*₍ А > 3.

Л (Индукция по t). При t = 3 лемма верна, так как Zg = {1,3,5,7}, ordl = 1, ord3 = ord5 = ord7 = 2. Пусть лемма верна для t > 3, докажем для t + 1.

По предположению индукции orda (mod2') 12^г~², где а = (1 + /e2^c)(mod2^r+1), к е {0, 1}. Тогда, возведя а в квадрат, получаем а² = l (mod2^r+1). Значит, ordfl (mod2^r+1) 12^,_1. Вместе с тем, любой /?eZ*,₊₎ имеет вид: h = а + к2^с, где aeZ‘"/ee {0,1}. Возведя в квадрат, имеем: Z)²(mod2^t+1) = (а + /г2')²(пкх12^г+1) = = c²(mod2^f+1) з l (mod2^f+1). Значит, ord/?(mod2^t+1) | 2^м. ?

Следствие. Не имеется первообразных корней по модулю т, отличному от 2, 4, р^к и 2р^к при простом нечетном р и к > 1.

•4 Если модуль от — не степень 2, то от = rs, где г > 2, s > 2 и (г, s) = 1, тогда ср (г) и ф (л) — четные числа. Используя теорему Эйлера, имеем: _ач>(т)/2 ₌ (_аФ (0)ч>(0/2 = l (modr) для любого а е Z'_m. Аналогично, яф («0/2 = = l (mods), тогда а<�р («0/2 = 1 (modm), так как (г, .v) = 1.

Если от = 2', f > 3, то по лемме 5.2 а²'"² = l (mod2'). ?

Первообразные корни можно находить, пользуясь утверждением.

Утверждение 5.7. Пусть а, (3, … — разные простые делители числа ф (от). При (а, от) = 1 число а — первообразный корень не верно ни одно из сравнений:

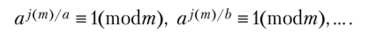
Л В циклической группе порядок образующего элемента равен порядку группы ф (от). Значит, порядок первообразного корня не может быть делителем числа ф (от). ?

Пусть Е, — первообразный корень по модулю от и у = 0, 1, …, ф (от) — 1 по модулю ф (от), тогда пробегает приведенную систему вычетов по модулю от, так как ?°, q,…, ?ф (^ш)-1 суть различные элементы группы (Е) порядка ф (от).

При (а, от) = 1 для числа а определен индекс или дискретный логарифм а, где основанием логарифма является Если а = ^(тойот), где у > О, то у называется индексом числа, а по модулю от при основании Е, обозначается у = ind"" или кратко у = inda. Отметим свойства:

• 1) любое а, взаимно простое с от, имеет единственный индекс среди О, 1,…, ф (от) — 1;
• 2) indaft = (inda + тй6)(тойф (от)); доказывается с помощью перемножения сравнений: а = ?'^пс|а(тойот) и b = ^'^пс16(тобот);
• 3) inda" = п ? тйа (тойф (от)); следует из свойства 2.

Используя таблицы индексов, показательные и степенные сравнения решают с помощью индексирования (дискретного логарифмирования), так как равносильны сравнения:

4) сравнение (5.9) разрешимо d = (п, ф (от)); число решений равно d.

Л По теореме 5.7 сравнение (5.9) разрешимо inda кратен d, число решений равно d. Равносильное сравнение (5.8) имеет d несравнимых по модулю от решений для х; ?

5) в приведенной системе вычетов по модулю от число вычетов степени п равно ф (от) / d; в этой системе вычетов имеется ф (от) / d чисел, кратных d.