Кольца, поля, векторные пространства

Множество R с бинарными операциями + и • называется кольцом, если:

• 1) /? — абелева группа относительно операции +;
• 2) операция умножения ассоциативна;
• 3) выполнены законы дистрибутивности, т. е. для всех a, b, с е R

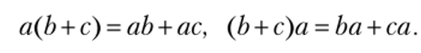
Нейтральный элемент аддитивной группы кольца называется нулем кольца (обозначается 0). Обратный элемент к а по сложению обозначается {-а).

Кольцо называется кольцом с единицей, если оно имеет мультипликативную единицу, т. е. элемент е, где ае = еа = а для любого а е R. Кольцо называется коммутативным, если операция умножения коммутативна.

Подкольцо кольца R — это подмножество R', являющееся кольцом, обозначается R' < R.

Правым {левым) идеалом кольца R называется его подкольцо R' (подкольцо L') со свойством R’R с R' {RL' с L'). Двусторонним идеалом или просто идеалом кольца R называется его подкольцо /?', являющееся правым и левым идеалом, т. е. R’R u RR' с R'.

Пример 2.4.

Кольца, подкольца, идеалы:

• а) Z — кольцо, mZ — идеал кольца Z при т е N;
• б) {0, 1} — кольцо, где сложение и умножение выполняются по модулю 2;
• в) Q — кольцо. О

Коммутативное кольцо называется полем, если его ненулевые элементы образуют группу относительно операции умножения. Иначе, ноле есть множество с операциями сложения и умножения, обладающими свойствами коммутативности, ассоциативности и дистрибутивности, где относительно обеих операций имеются нейтральные элементы и любой элемент а (любой b Ф 0) обратим относительно операции сложения (умножения).

Пример 2.5.

Полями являются множества Q, R, {0, 1} с операциями по модулю 2. О Уравнение вида ах + b = с разрешимо в поле Р для любых а, b, с е Р и в кольце R с единицей для любых b, с е R и для обратимого элемента а: х = а~^х(с — Ь).

Пусть Р — поле, и на множестве V заданы внутренняя бинарная операция сложения и операция умножения элементов на элементы поля, где результат умножения принадлежит V. Множество V называется векторным пространством над нолем Р, а его элементы — векторами, если V — абелева группа относительно + и для любых а, (3 е Р и х, у е V выполнено:

• 1) Ох = 0, где 0 е Р, 0 е V, где 0 — нуль пространства;
• 2) 1х = х, где 1 е Р;
• 3) (а (3)х = a ((ir);
• 4) (а + (3)х = ах + $х;
• 5) а (х + у) = ах + аг/.

Вектор apq + … + a_fJx_ni где ctj, а" е Р, называется линейной комбинацией векторов x_lf …, из V. Линейная комбинация векторов называется тривиальной, если оц = … = а_и = 0, и нетривиальной — в противном случае.

Система векторов {x_if…, х_п} линейно зависимая, если имеется нетривиальная линейная комбинация векторов, равная 0, и линейно независимая в противном случае.

Пространство Vназывается п-мерным, а п — числом измерений, или ряз- мерпостыо пространства V (обозначается dim У = п), если в У существуют п линейно независимых векторов, а любые п + 1 векторов из V линейно зависимы.

Если в пространстве V имеется линейно независимая система из любого числа векторов, то пространство V называется бесконечномерным.

Система {х_{,…, х_п} линейно независимых векторов /г-мерного пространства называется базисом пространства. Любой элемент пространства V представляется однозначно в виде линейной комбинации элементов базиса: х = а_{х_х + … + а_Г1х_п. Элементы поля …, а_п называются координатами вектора х в базисе {х_{, …, х_п}. При разных базисах координаты вектора х в общем случае различны.

Пример 2.6.

Векторными пространствами являются множества:

а) слова (сс₀,…, ot^) длины п над полем Р (обозначается Р¹), сложение векторов определено формулой: (а₀,…, а,_м) + (р₀, …, = (а₀ + р₀, …, a_n__t + р^), и умно;

жение вектора на скаляр Р (элемент поля) определено формулой: P (oCq, а_п_,) = = (ра₀, pa"__t). Пример базиса пространства Р^п — система п векторов, где в i-м векторе на i-м месте записана 1 е Р, а остальные элементы равны 0, i = 1,п;

6) бесконечные последовательности над Р, пример базиса — система последовательностей, где в i-Pi последовательности на i-м месте записана 1, а на других местах О, /=1,2, …>

Подмножество V' пространства V, являющееся пространством, называют подпространством пространства V. Подмножество V', замкнутое относительно обеих операций, образует подпространство, при этом dimV' < dim V. Пересечение подпространств есть подпространство.

Если ЯсУ, то наименьшее подпространство V' пространства V, содержащее в качестве подмножества Я, т. е. ЯсУ’с V, называют линейной оболочкой множества Я или подпространством, порожденным множеством Я. Это подпространство (обозначается (Я)) состоит из всевозможных линейных комбинаций векторов множества Я. Базисом пространства (Я) является, в частности, максимальная линейно независимая подсистема множества Я.

Биекция ф: V <-" V' между пространствами V' и V над полем Р называется изоморфизмом пространств, если изоморфны соответствующие абелевы группы и ф (осг) = аф (.г) для любых, а е Р и х е V. При этом dimV" = dim К.