Решение задачи Дирихле для уравнения Лапласа

Еще один наглядный пример применения метода статистических испытаний — решение задачи Дирихле для уравнения Лапласа с использованием алгоритма «блужданий, но сетке». Строгое обоснование этих алгоритмов можно найти в классических работах по методу Монте-Карло.

Напомним, что уравнением Лапласа называется уравнение в частных производных.

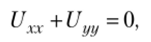
задачей Дирихле для уравнения Лапласа — задача нахождения функции, удовлетворяющей уравнению Лапласа в ограниченной связной области D и граничным условиям.

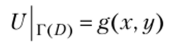
на границе области 1(D).

Сформулируем задачу следующим образом: требуется применить статистическое моделирование для вычисления значения в точке Л (0,8; 0,6) функции U> удовлетворяющей в квадрате D = {Q 0 < г/ < 1} уравнению Лапласа и на границе квадрата — граничным условиям.

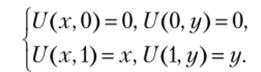
Для вычисления U (A) введем в области {0<�х<1, 0< г/<1} квадратную сетку с шагом h = 0,2. В практических задачах шаг сетки выбирают достаточно малым, поскольку от него зависит погрешность, возникающая при замене границы области сеточным контуром. В нашем учебном примере возьмем шаг крупным для удобства вычислений. Узлы сетки пронумеруем таким образом, чтобы пара номеров (i, j) соответствовала точке (x_jf i/j), Xj = ih, i = 0,1,…, 5, Uj = jh, j = 0,1,…, 5 (рис. 2.22).

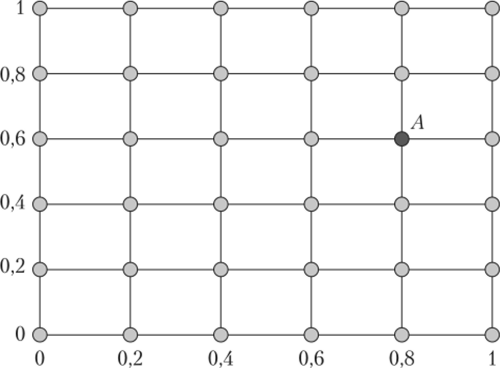
Рис. 2.22. Сеточная область, аппроксимирующая квадрат {0<�лг< 1, 0 <�у< 1}.

Значение функции в узле (г, у) обозначим _;. С помощью разностных аппроксимаций производных во внутренних узлах.

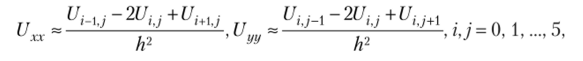
приведем уравнение Лапласа к виду.

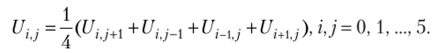
Алгоритм «блужданий, но сетке» построим следующим образом.

• 1. Начало траектории «блуждания» поместим в точку А (0,8; 0,6), т. е. в узел (4, 3).
• 2. Очередной шаг из узла (i, j) делается в узел:
  • (г, у + 1) с вероятностью р_{ = 0,25;
  • (г, у — 1) с вероятностью р₂ = 0,25;
  • (г + 1,7) с вероятностью р₃ = 0,25;
  • (г — 1,7) с вероятностью р_А = 0,25.
• 3. Если новый узел (г, у) внутренний, то повторяем шаг 2, т. е. делаем очередной шаг траектории, если узел (г, у) граничный, то траектория «блуждания» обрывается, граничное значение ?/,• •, соответствующее той граничной точке, в которой оборвалась траектория, считается выборочным значением случайной величины

Доказано, что с вероятностью 1 траектория за конечное число шагов достигнет границы области. Таким образом, построив требуемое число траекторий «блуждания по сетке», можно вычислить приближенное значение решения.

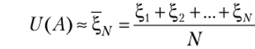
и оценить его погрешность, но формуле (2.20).

Выполним расчет, используя случайные числа, полученные с помощью датчика псевдослучайных чисел rand системы MATLAB.

Очередной шаг «блуждания» будем делать в узел:

• (г, у + 1), если случайное число принадлежит промежутку [0; 0,25);
• (г, у — 1), если случайное число принадлежит промежутку [0,25; 0,5);
• (г + 1,7), если случайное число принадлежит промежутку [0,5; 0,75);
• (г — 1,7), если случайное число принадлежит промежутку [0,75; 1). Первые две траектории «блуждания», полученные по такому алгоритму, изображены на рис. 2.23. Покажем, как построены эти траектории (в скобках над стрелкой указывается случайное число, в соответствии с которым осуществляется переход в следующий узел):
  • 1) (4,3) —(°-^j226> _>(5_> 3) — конец первой траектории;
  • 2) ₍₄,₃₎ <�°-⁸⁸°0 >(3,3) ^((Ш30) >(3,4) ⁽⁰'⁹⁷⁹⁷⁾ >(2,4) ⁽⁰'²⁷¹⁴⁾ >
• (0'^{27|4) >(2,3) <2 523) >(2,2) <�°-8757) >(1,₂) (0-7373) >}
• (0,7373) 2) («1365) g) (0.0118) 4) (0.8939) ₎
• —⁽⁽⁾'⁸⁹³⁹⁾ >(1,4) —^(0,1991) >(1,5) — конец второй траектории.

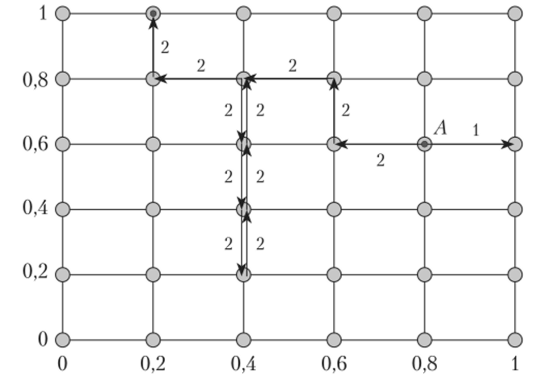
Рис. 2.23. Две траектории алгоритма «блужданий по сетке»

Полученные по такому алгоритму 10 значений случайной величины? оказались равными 0,3980, 0,0000, 6,5940, 0,7726, 0,5881, 0,3941, 0,5823, 0,0000, 0,5794, 0,9561.

По формулам (2.19), (2.21), (2.22) получим.

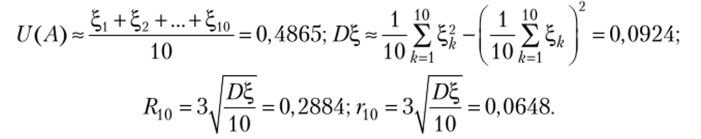
Обратите внимание!

При оценке погрешности решения задачи Дирихле для уравнения Лапласа с использованием статистического моделирования следует иметь в виду, что она складывается из погрешности разностного метода, определяемой шагом сетки, и статистической оценки погрешности, возникающей при реализации статистических испытаний.