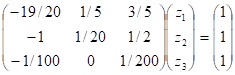Заключение. 
Понятие приближенного решения некорректно поставленных задач

Для реализации численного примера был выбран метод Тихонова решения плохо обусловленных СЛАУ. В качестве исходной была взята СЛАУ Az=u, имеющая в матричной записи вид:

Определитель матрицы коэффициентов этой системы близок к нулю — он равен 0.125. Попробуем решить эту систему с помощью обратной матрицы:

z=A^-1u.

Получим z₁=316.

z₂=-990.

z₃=832.

Теперь предположим, что правая часть нам известна приближенно, с погрешностью 0.1 Изменим, к примеру, третий элемент вектора-столбца с 1 на 1.1 :

Попробуем решить новую систему также с помощью обратного оператора. Мы получаем другой результат:

z₁=348.

z₂=-1090.

z₃=916.

Мы видим, что малому изменению правой части данной системы отвечают весьма значительные изменения решения. Очевидно, эта система — плохо обусловленная, и здесь не может идти речи о нахождении решения близкого к точному с помощью обратного оператора.

Будем искать решение методом Тихонова. В теоретической части было показано, что целесообразно использовать регуляризирующий оператор следующего вида:

(aE + A^TA)z^a=A^Tu_d ,.

где E — единичная матрица, z^a———приближенное нормальное решение, A^T — транспонированная исходная матрица, a———параметр регуляризации,.

u_d — —правая часть, заданная неточно. Эту задачу можно решать стандартными методами, задав предварительно функцию a=a (d)—,—удовлетворяющую условиям теоремы Тихонова. В моем примере это функция a (d)=d/4^d.—Далее будем решать регуляризованную задачу с точностью e=_.001, последовательно изменяя значения a.

В качестве контр-примера можно подставить в программу любую функцию a (d), не удовлетворяющую условиям теоремы Тихонова. Любая положительная функция монотонно возрастающая, не обладающая свойством a (d)0 при d0, не будет минимизировать невязку.

Текст программы приведен в приложении 1. Полная распечатка результатов приведена в приложении 2. Здесь же представлены окончательные значения на выходе из программы.

Приближение к нормальному решению.

Z (1)= 3.4 783 481 917 4013E+0002.

Z (2)=-1.894 839 497 5175E+0003.

Z (3)= 9.1 556 644 313 7791E+0002.

Значение правой части при подстановке прибл. решения.

U1(1)= 9.9 999 771 701 2495E-0001.

U1(2)= 1.74 197 0775E+0000.

U1(3)= 1.994 840 239 4883E+0000.

Значение параметра регуляризации:

2.61 934 474 110 603 E-0010.