Определение углов полной рефракции при больших зенитных расстояниях

Обычно при получении формул углов рефракции полагают, что атмосфера является сферической, и слои газовой среды или воздуха одинакового коэффициента преломления (изодиоптрические слои) являются сферами с центром, совпадающим с центром Земли. Полагаемое для такой модели дифференциальное уравнение угла полной рефракции имеет вид:

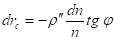
(1).

где ц — угол между радиусом сферы и направлением оптического луча в текущей точке; n — коэффициент преломления газовой среды или воздуха, с" = 206 265″ [1].

Недостатком этого уравнение является то, что при ц = 900 dц = ?, хотя известно, что в горизонте угол астрономической рефракции равен не бесконечности, а примерно 35'. Поэтому выражение (1) используют обычно при углах ц, отличающихся от 900. Кроме того, при статическом состоянии атмосферы изодиоптрические поверхности обычно совпадают с уровенными, положение которых в пространстве более точно аппроксимируется поверхностями, параллельными поверхности Земного эллипсоида. Поэтому при определении углов рефракции необходимо учитывать и это обстоятельство.

Для больших зенитных расстояний целесообразно получить дифференциальное уравнение рефракции, свободное от этих недостатков. В первую очередь получим выражение, которое позволяло бы определять углы рефракции при любых зенитных расстояниях, включая и 900.

В инварианте Снеллиуса.

(2).

Примем.

.

Тогда.

.

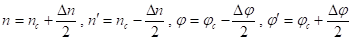
С учетом этих значений инвариант Снеллиуса примет вид.

.

После преобразований имеем.

. (3).

Полученная формула является строгой и ее можно использовать при любых значениях ц. Учитывая малое значение Дц, можно принять.

.

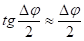
Тогда, принимая во внимание.

.

где N — индекс преломления,.

.

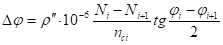
Угол полной рефракции.

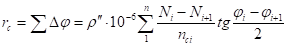
(4).

где.

— индекс преломления.

Для определения входящих в формулу (4) углов цi, цi+1 в сферической модели атмосферы используют известный инвариант, откуда.

(5).

Где.

а1 — расстояние от центра Земли до начальной точки траектории оптических волн, аi — до текущей точки i; n1, n — коэффициенты преломления в начальной и текущей точках соответственно; ц1, ц — углы между нормалью к изодиоптрической поверхности и траекторией луча в начальной и текущей точках.

Более строго атмосферные слои целесообразно аппроксимировать эллипсоидами вращения, изодиоптрические слои которых параллельны поверхности Земного эллипсоида, т. е. слои эллипсоидальной атмосферы совпадают с уровенными поверхностями.

Для эллипсоидальной атмосферы необходимо учитывать следующее обстоятельство. Радиус кривизны нормального сечения определяют по формуле.

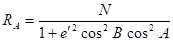
(6).

где радиус кривизны первого вертикала.

. (7).

В формулах (6), (7) е2 и е'2 — квадраты первого и второго эксцентриситетов эллипса; а, с — радиус кривизны экватора и полярный радиус кривизны; В — геодезическая широта; А — азимут нормального сечения.

Значения RA, вычисленные по формуле (6) для различных значений широты В и азимута А, показали, что максимальная разность RA достигает 64,146 км в плоскости меридиана. Выясним, на каком расстоянии от пункта наблюдения оптический луч будет выходить из атмосферы. Известно, что на высоте 30 км в стандартной атмосфере ГОСТ 4401–81 давление р = 1,93 гПа, Т = 226,509 К. На уровне моря р0 = 1013,25 гПа, Т0 = 288,15 К, N0 = 278,24. С учетом этих значений.

.

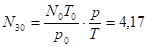
На высоте 40 км р = 0,287 гПа, Т = 250,350 К, а значение N40 = 0,091.

Следовательно, на высотах более 30 км атмосфера является разреженной и определение углов рефракции в слое 30 — 100 км можно принимать сферическую модель атмосферы с радиусом кривизны RA на высоте 30 км. Для слоев одинакового коэффициента преломления, параллельных поверхности с изменяющимся радиусом кривизны целесообразно получить формулу, позволяющую определять углы ц между нормалью к этой поверхности и направлением оптического луча. Положим, что для элементарного участка трассы электромагнитных волн атмосфера является сферической. Тогда для участка трассы имеем.

.

для отрезка.

1 — 2 ,.

для отрезка.

2 — А .

Подставляя из последнего выражения.

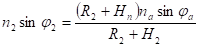
во второе, получим.

.

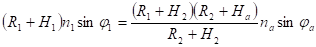
Подставляя из полученного выражения в первое, находим.

.

Или.

.

После небольших преобразований с учетом величин первого порядка малости имеем сферический преломление изодиоптрический рефракция.

.

Учитывая бесконечно малые отрезки трассы электромагнитных волн G — 1, 1 — 2, …, n — A, получим.

. (8).

Используя при интегрировании теорему о среднем значении, находим.

. (9).

Значения N для изотермической атмосферы, в которой температура с высотой изменяется по линейному закону, вычисляют по формуле.

.

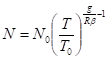
Сравнение значений rc, вычисленных по формуле (4) для цg = 890 и цg = 900 и условий стандартной атмосферы ГОСТ 4401–81 численным интегрированием с шагом по высоте 0,25 км и путем удвоения шага (0,50 км) показало, что разности значений rc не превышают для цg = 890 0,15″, а для цg = 900 при Н через 0,1 км и для Н через 0,2 км, практически дают одинаковые результаты (разности не превышают 0,07″), что свидетельствует о высокой точности полученной формулы и ее возможности определять углы rc при любых значениях цg, включая и цg = 900. т. е. точность определения углов rc является достаточно высокой.

• 1. В. И. Куштин. Учет влияния атмосферы на результаты измерения длин радиоэлектронными системами. Монография. Москва, МИИГАиК, 2003, 179с.
• 2. Атмосфера стандартная. Параметры ГОСТ 4401–81.-М.: Издательство стандартов, 1981, 280с.