Метод последовательных разностей

Этот метод применим для обнаружения изменяющейся во времени систематической погрешности. Дисперсию результатов наблюдений можно оценить двумя способами:

Обычным.

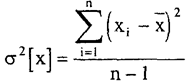
(4.1).

или вычислением суммы квадратов последовательных (в порядке последовательности измерений) разностей.

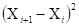
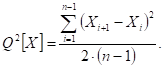
(4.2).

Если в процессе измерений происходило смещение центра группирования результатов наблюдений, т. е. имела место временная систематическая погрешность, то даёт преувеличенную оценку дисперсии результатов наблюдений. Это объясняется тем, что на влияют вариации. В то же время изменения центра группирования весьма мало влияют на последовательные разности, и смещения почти не отразятся на значении. Вследствие этого отношение.

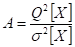
(4.3).

является критерием для обнаружения систематических смещений центра группирования результатов наблюдений.

Критическая область для этого критерия (критерия Аббе) определяется как. Значения для различных уровней значимости и чисел наблюдений «n» приведены в таблице 4.1. Если полученное значение критерия Аббе меньше при заданном и «n», то нулевая гипотеза о постоянстве центра группирования результатов наблюдений отвергается, т. е. обнаруживается переменная систематическая погрешность (СП) результатов измерений (таким образом: если Aб, то СП есть).

Значения критерия Аббе Таблица 4.1.

Для заданного в задании ряда результатов измерений линейного размера L элемента конструкции строящегося здания (см. таблицу № 2. 1) вначале вычислим среднее арифметическое значений этого ряда:

(м). (4.4).

Полученное среднее арифметическое значение, как и другие промежуточные результаты для применения критерия Аббе, сведены в таблицу 4.2.

Таблица 4.2.

Промежуточные результаты для применения критерия Аббе.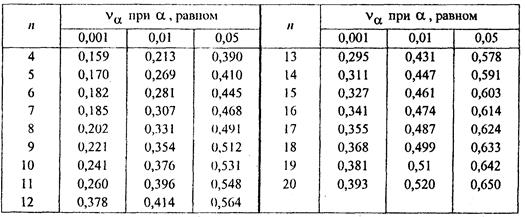

№ измерения.	X=Li, м.
		;	;	— 0,6.	0,36.
		— 2.		— 2,1.	4,41.
		— 5.		— 6,6.	43,56.
				2,4.	5,76.
		— 8.		— 5,1.	26,01.
				— 0,6.	0,36.
				0,9.	0,81.
		— 5.		— 3,6.	12,96.
				— 0,6.	0,36.
		— 2.		— 2,1.	4,41.
				0,9.	0,81.
				2,4.	5,76.
		— 3.		— 0,6.	0,36.
				3,9.	15,21.
		— 2.		2,4.	5,76.
				5,4.	29,16.
		— 6.		— 0,6.	0,36.
		— 2.		— 2,1.	4,41.
		— 2.		— 3,6.	12,96.
		— 5.		— 8,1.	65,61.
				— 5,1.	26,01.
				— 2,1.	4,41.
				— 0,6.	0,36.
				2,4.	5,76.
				3,9.	15,21.
		— 2.		2,4.	5,76.
				6,9.	47,61.
		— 5.		2,4.	5,76.
				3,9.	15,21.
				3,9.	15,21.
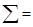		380,7.

Используя выражение (4.2) и суммарный результат 4-го столбца таблицы 4.2, определим значение дисперсии :

.

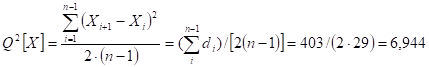
Применяя выражение 4.1 и суммарный результат 6 -го столбца таблицы 4.2, определим значение дисперсии :

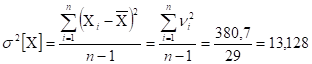
Тогда расчётное значение критерия Аббе с использованием выражения 4.3, будет равно:

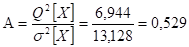
Сравнивая расчётные значения критерия Аббе «А=0,529» с табличными «» из таблицы 4.1. при трёх уровнях значимости () и при «n=20» (максимальное значение числа измерений в таблице 4.1 и наиболее близкое для исследуемых результатов измерений «n=30») можно сделать следующий вывод: для уровней значимости (доверительных вероятностей) (0,529>0,393) и (0,529>0,520) выполняется неравенство A>A_б, что свидетельствует об отсутствии систематической погрешности в результатах измерений, а при уровне значимости выполняется неравенство A.