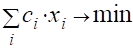Определение кратчайшего остова неориентированного графа на основе упорядочения ребер графа (алгоритм Прима-Краскала)

Такая задача возникает при прокладке дорог, газопроводов, линий электропередач и т. д., когда необходимо связать n точек так, чтобы общая длина «линий связи» была минимальной. Следует отметить, что «кратчайший остов графа» не имеет никакого отношения к дереву, дающему все кратчайшие пути, выходящие из некоторой выбранной вершины. Так, для графа (рис. 3.4), где числа, стоящие около ребер, являются их весами, дерево, дающее все кратчайшие пути, выходящие из вершины х₁, изображено на рис. 3.5, а кратчайший остов графа представлен на рис. 3.6.

X1.

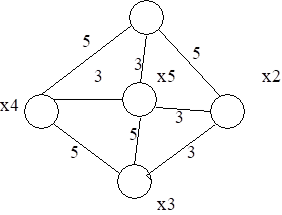
Рис. 3.4.

X1.

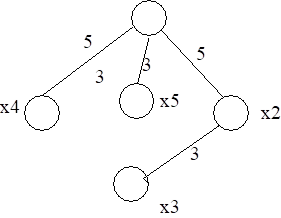
Рис. 3.5.

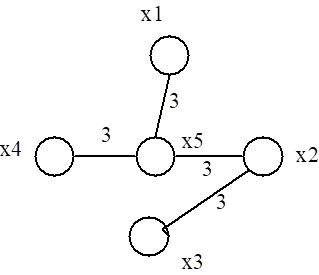
Рис. 3.6.

Итак, кратчайший остов графа связывает кратчайшим образом все вершины графа, а не только х₁ с другими вершинами.

Для построения кратчайшего остова с помощью алгоритма, изложенного в п. 3.5.3, необходимо в п. 2 сформировать последовательность ребер в порядке возрастания их весов.

Решение задачи о кратчайшем пути в графе на основе линейного программирования [1,4]

Рассмотрим решение задачи на примере исходного графа, изображённого на рис. 3.7. Необходимо для него сформировать минимальное остовное дерево.

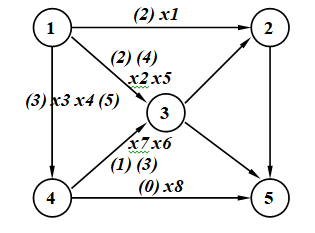
Рис. 3.7 Исходный граф

Решать данную задачу, как задачу линейного целочисленного программирования. Для этого необходимо сформировать целевую функцию и ограничения, накладываемые на переменные.

Ограничения записываются следующим образом.

Для исходной вершины: ,.

где все xi выходят из исходной вершины, а N число вершин графа.

Для остальных вершин: сумма дуг (переменных), прилегающих к рассматриваемой вершине, равна единице, причём дуги, входящие в вершину, берутся со знаком «+», а выходящие со знаком.

««.

Вид целевой функции будет следующим:

.

где значения коэффициентов целевой функции Сi характеризуют стоимости потоков (рис. 3.7) .

На переменные xi необходимо наложить условия неотрицательности и целочисленности.

Cистема ограничений и целевая функция для данной задачи имеют вид:

x1 + x2 + x3 = 4.

x1 + x5 x4 = 1.

x2 x5 x6 + x7 = 1.

x3 x7 x8 = 1.

x4 + x6 + x8 = 1.

xi 0.

xi целые F = 2×1 + 2×2 + 3×3 + 5×4 + 4×5 + 3×6 + x7 + 0×8 min.

Решение задачи имеет вид:

x1 = 1.

x2 = 1.

x3 = 2.

x4 = 0.

x5 = 0.

x6 = 0.

x7 = 0.

x8 = 1.

Fmin = 10.

В этом случае получаем граф оптимального решения, изображённый на рис. 3.8.

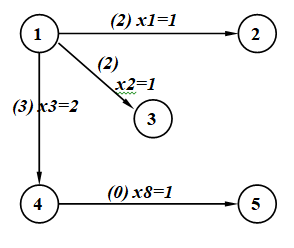
Рис. 3.8. Граф оптимального решения.

Дуги, не принадлежащие остовному дереву, имеют поток по ним равным нулю (переменные X_i=0) .