Дисперсионный анализ. 
Политический анализ и прогнозирование в 2 ч. Часть 2

Дисперсионный анализ (английское название «ANalysis Of VAriance», ANOVA) является одним из основополагающих статистических методов. Важность умения работать с его алгоритмами определяется не только теми возможностями, которые дисперсионный анализ предоставляет исследователю как самостоятельный метод анализа данных. Сравнение дисперсий переменных входит во многие более сложные статистические методы, например в регрессионный анализ. Кроме того, это хороший пример практического использования проверки статистических гипотез (см. главу 5).

Одна из основных задач, решаемых дисперсионным анализом, — проверка гипотезы о статистической значимости различий между средними значениями в нескольких группах наблюдений. Например, имеется гипотеза о влиянии фактора урбанизации (А) на поддержку либеральных партий (Y). В качестве объектов анализа выступают территории — города и районы. Каждая территория характеризуется двумя признаками: урбанизацией и уровнем поддержки либеральных партий.

Признак «урбанизация» может быть операционализирован несколькими способами. Первый заключается в том, чтобы измерять долю (или процент) городского или сельского населения, в результате чего мы получим параметрический показатель. Такой стратегией мы воспользуемся, когда будем изучать корреляцию и регрессию, ориентированные на работу с параметрами. Для дисперсионного анализа, который работает с группами наблюдений, уместен другой подход, — представить урбанизацию как номинальную переменную с двумя значениями: 1 — сельская территория, 2 — городская территория. Фактически, в соответствии с правилами номинального измерения, мы формируем два непересекающихся класса (группы) территорий — сельские и городские. Что касается поддержки либеральных партий, то здесь мы будем использовать суммарный процент голосов, отданных за них на последних парламентских выборах (исходные данные см. в табл. 7.1).

Таблица 7.1

Для математического описания модели дисперсионного анализа прибегнем к использованию формальной записи вида Уу, где у — процент поддержки либеральных партий, индекс У показывает номер территории: У = 1,2, …, п. Индекс j указывает принадлежность наблюдения к одной из выделенных групп, всего групп к к = 1,2, …, к. В нашем случае групп всего две — городские и сельские территории, т. е. к = 2. Например, в табл. 7.1 третий объект можно записать как у₃| =6.

Проведя описательный статистический анализ обеих групп, мы обнаружим, что они существенно различаются по средним значениям переменной «поддержка либеральных партий». Избиратели сельских территорий в среднем значительно менее охотно голосуют за либералов, нежели избиратели городских территорий: средние арифметические У и у₂ составляют 4% и 12% соответственно.

Теперь мы должны ответить на следующий вопрос. Насколько значимо различие между средними значениями в двух группах, не является ли это различие случайным? Другими словами, насколько вероятно, что городские избиратели в среднем отличаются своим отношением к либеральным политическим партиям от сельских не только в нашей выборке (где очевидно, что уу ф у₂), но и в генеральной совокупности (р, ф р₂)?

Сформулируем две гипотезы, нулевую и альтернативную. Нулевая гипотеза гласит, что различия средних являются случайными, зависимость между переменной «принадлежность к городскому населению» и переменной «поддержка либеральных партий» отсутствует:

Альтернативная гипотеза содержит противоположное утверждение:

Логика дисперсионного анализа базируется на сопоставлении дисперсий двух типов. Во-первых, это межгрупповая дисперсия, обусловленная колебаниями средних значений в группах по отношению к общей средней, рассчитанной без учета группировки наблюдений. Величина межгрупповой дисперсии будет тем больше, чем больше различаются средние значения групп, другими словами — чем более точен группирующий признак. Во-вторых, это внутригрупповая дисперсия, обусловленная колебаниями наблюдений внутри групп. Такие колебания обусловлены случайными с точки зрения группирующего признака факторами. Требуется понять, насколько колебания переменной, обусловленные разбиением на группы, сильнее случайных колебаний, не связанных с группирующим признаком. Другими словами, требуется найти отношение межгрупповой дисперсии к внутригрупповой дисперсии. Это отношение Фишера, или /?" -отношение, названное так в честь создателя метода — Рональда Фишера:

где а? и а₂ — межгрупповая и внутригрупповая дисперсии соответственно.

Чем больше это отношение, тем существеннее различие групповых средних и значительнее влияние группирующего признака.

Вычислительный аппарат дисперсионного анализа основан на одном очень важном разложении. Так, отклонение наблюдения от обшей средней может быть представлено как сумма двух компонент: 1) отклонения наблюдения от групповой средней и 2) отклонения групповой средней от общей средней:

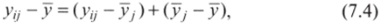
где У) — средняя в группе.

Так, на рис. 7.1 отображены значения поддержки либералов в сельских территориях (группа 2); сплошной линией показана групповая средняя (4%), пунктирной — общая средняя (8%). Например, отклонение пятого наблюдения от общей средней по формуле (7.4) составит:

Рис. 7.1.

Теперь нам понадобится более сложное разложение, обобщающее (7.4):

Первое слагаемое¹ в правой части представляет собой внутригрупповую дисперсию, второе — межгрупповую дисперсию. В сумме они формируют общую дисперсию переменной (левая часть):

Суммарная дисперсия = внутригрупповая дисперсия + межгрупповая дисперсия.

Разберем эту пугающего вида формулу в деталях. Сначала рассчитаем по шагам суммарную дисперсию данных (левая часть 7.5).

Упражнение 7.1

• 1. Для удобства работы организуем данные из таблицы (доступна по ссылке http://polit.msu.ru/kaf/lab_quant/) следующим образом. В первый столбец листа Excel поместим данные по сельским территориям (группа 1), во второй — по городским (группа 2).
• 2. Рассчитайте общую среднюю арифметическую у, используя функцию «=СРЗНАЧ». Результат должен составить 8. Не забудьте, что аргументами этой функции должны быть наблюдения из обеих групп! Все функции показаны на рис. 7.2.
• 3. Рассчитайте отклонения наблюдений в первой группе от общей средней — у_п — у.
• 4. Возведите получившиеся разности в квадрат —
• (у_л — у)², используя функцию «=СТЕПЕНЬ».
• 5. Суммируйте квадраты отклонений наблюдений в первой группе от общей средней — 096, используя функцию «=СУММ». В результате получится 252.
• 6. Рассчитайте отклонения наблюдений во второй группе от общей средней — у_а — у.
• 7. Возведите получившиеся разности в квадрат —
• (Уа-У)².

'Двойной оператор суммирования IX показывает, что сначала складываются случаи внутри групп (правая сигма), а затем — суммы по группам (левая сигма).

8. Суммируйте квадраты отклонений наблюдений во.

П₂

второй группе от общей средней — ^(Уп~У)². Результат составит 260. ¹⁼¹

9. Сложите сумму квадратов отклонений от общей средней в первой группе и сумму квадратов отклонений от общей средней во второй группе:

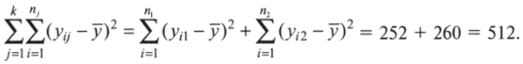
Вы получили суммарную дисперсию данных.

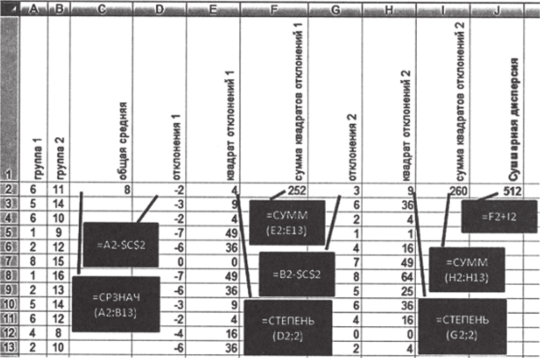
Рис. 7.2.

Теперь рассчитаем внутригрупповую дисперсию (функции см. на рис. 7.3).

Упражнение 7.2

• 1. Рассчитайте среднюю в первой группе — у. Результат составит 4.
• 2. Рассчитайте отклонения наблюдений в первой группе от групповой средней — у_п — у.
• 3. Возведите получившиеся разности в квадрат —

О'/I «уУ4. Суммируйте квадраты отклонений в первой группе от.

П,

групповой средней — ^(у,| -у))² В результате получится 60.

/=1.

• 5. Рассчитайте среднюю во второй группе — у₂. Результат составит 12.
• 6. Рассчитайте отклонения наблюдений в первой группе от групповой средней — у_а — у_г.
• 7. Возведите получившиеся разности в квадрат — (Уа ~ Уг)²-
• 8. Суммируйте квадраты отклонений наблюдений во

П_:

второй группе от групповой средней — ^(у, 2^-у)². Результат составит 68. ¹⁼¹

9. Сложите сумму квадратов отклонений от групповой средней в первой группе и сумму квадратов отклонений от групповой средней во второй группе:

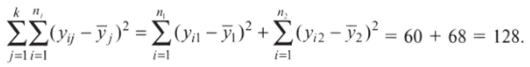
Вы получили внутригрупповую дисперсию данных. В англоязычной и переводной литературе часто используется также запись 55 error (sum of squared errors — сумма квадратов ошибки).

Рис. 7.3.

Рассчитаем межгрупповую дисперсию.

Упражнение 7.3

1. Рассчитайте отклонение средней первой группы от общей средней — — у. Получится -4.

• 2. Возведите полученное отклонение в квадрат — (у, — у)². Получится 16.
• 3. Умножьте квадрат отклонения на число наблюдений в первой группе — (ё| — у)²я,. У нас 12 объектов, и результат составит 192.
• 4. Рассчитайте отклонение средней второй группы от общей средней — у₂ — у. Получится 4.
• 5. Возведите полученное отклонение в квадрат — (у₂ ^— У)²— Получится 16.
• 6. Умножьте квадрат отклонения на число наблюдений во второй группе; их столько же, сколько и в первой, — (у₂ — у)²п₂. Результат составит 192.

Вообще говоря, в дисперсионном анализе группы не обязательно должны быть одинаковыми по числу наблюдений, как в нашем примере. Если бы выборки были разными по объему, в результате выполнения операций в п. 3 и п. 6 мы получили бы разные числа.

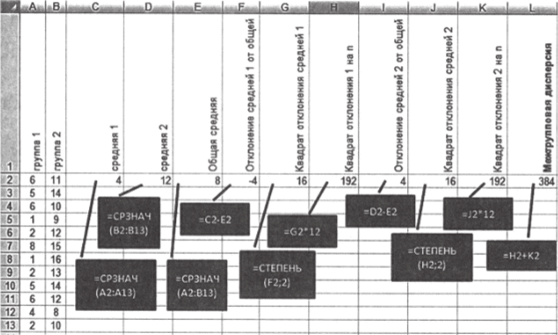
Рис. 7.4.

7. Суммируйте результаты п. 3 и п. 6, в результате получится 384. Мы получили межгрупповую дисперсию —

к

Х (?, -У)Ч ⁼Си ~У)^{1п +}(У2 ~У)^1п2. В англоязычной лите;

i=1.

ратуре — SS effect (sum of squared effect — сумма квадратов эффекта).

Итак, у нас есть возможность проверить справедливость равенства (7.5):

Что еще более важно, у нас имеется почти все необходимое для расчета отношения Фишера (7.3). «Почти» — потому что для выполнения дисперсионного анализа нам потребуется еще одно понятие — понятие степеней свободы. Напомним, что для одномерных распределений число степеней свободы рассчитывается по формуле:

где п — общее число наблюдений.

Так, в нашем примере для каждой группы по отдельности мы имеем 12−1 =11 степеней свободы. При расчете межгрупповой дисперсии степени свободы рассчитываются по формуле.

где к — число групп.

В нашем примере df_x = 2 — 1 = 1.

Для расчета внутригрупповой дисперсии используется формула

где п — число наблюдений, к — число групп.

В нашем примере df₂ = 24 — 2 = 22 (это число равно сумме степеней свободы каждой из групп: 11 + 11= 22).

Межгрупповую и внутригрупповую дисперсии требуется скорректировать на соответствующие числа степеней свободы, и мы получим окончательные формулы их расчета. Итак, межгрупповая дисперсия:

В статистических программах для межгрупповой дисперсии, скорректированной на степени свободы, используется также запись «MS effect» (mean square effect — средний квадрат эффекта).

Внутригрупповая дисперсия:

Для нее также используется обозначение «MS error» (mean square error — средний квадрат ошибки).

В нашей задаче межгрупповая дисперсия составляет 384/1 = 384. Внутригрупповая дисперсия составляет 128/22 = 5,8.

Отношение Фишера (7.3):

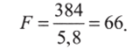
Выше мы говорили о том, что чем больше F, тем существеннее различие групповых средних. Но насколько велико рассчитанное нами значение — 66?

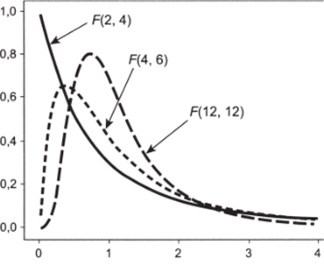
Рис. 7.5.

Для ответа на этот вопрос используется специальное распределение — распределение Фишера, или /'-распределение. Его управляющими параметрами являются числа степеней свободы межгрупповой и внутригрупповой дисперсии. Распределение обладает правой асимметрией; чем больше значения df_{ и df₂, тем более симметричной становится функция плотности вероятности (рис. 7.5'; в скобках указаны степени свободы df и df₂).

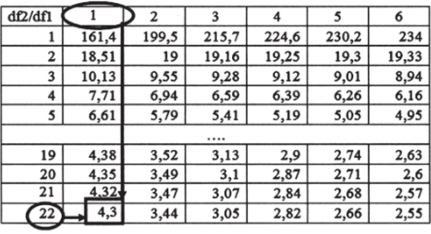
Для поиска критических значений воспользуемся таблицей^[1]

распределения и функцией Excel. Начнем с таблицы: мы приводим здесь небольшой ее фрагмент (см. табл. 7.2).

Критическое значение зависит от степеней свободы межгрупповой и внутригрупповой дисперсии, которые в нашем случае составляют 1 и 22 соответственно. Первое число находим в столбцах, второе — в строках.

Таблица 7.2

То же критическое значение можно получить, используя функцию Excel «=FPACnOBP». Эта функция имеет три аргумента:

• • вероятность — уровень статистической значимости;
• • степени свободы 1 — степени свободы межгрупповой дисперсии;
• • степени свободы 2 — степени свободы внутригрупповой дисперсии.

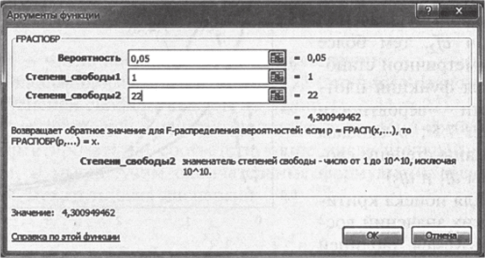
Рис. 7.6

Несмотря на то, что нулевая гипотеза (7.1) сформулирована в форме равенства, в дисперсионном анализе достаточно правосторонней проверки: для отклонения нулевой гипотезы рассчитанное^должно быть больше критического значения. Это и имеет место в нашем примере: 66 > 4,3 (рис. 7.7).

Рис. 7.7.

Таким образом, мы принимаем альтернативную гипотезу. В результате анализа мы убедились, что разделение территорий на городские и сельские влияет на средний уровень поддержки либеральных партий.

Дисперсионный анализ может быть целиком реализован в программе Excel. Для этого используется надстройка «Анализ данных» — «Однофакторный дисперсионный анализ» (см. рис. 7.8). Слово «однофакторный» означает, что имеется только один группирующий признак, в нашем случае — принадлежность к городскому или сельскому населению.

Рис. 7.8.

В меню дисперсионного анализа следует указать входной интервал, наличие названий групп в первой строке, и ауровень (см. рис. 7.9).

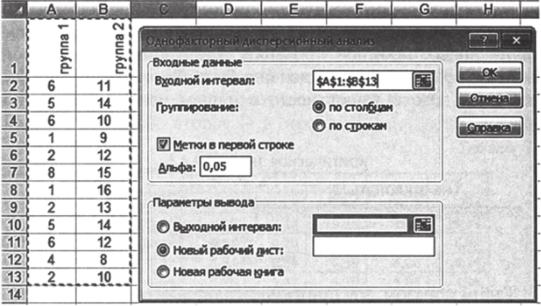
Рис. 7.9.

Результаты дисперсионного анализа Excel формирует в виде таблицы на отдельном листе.

Таблица 7.3

Напомним, что аббревиатура SS относится к межгрупповой и внутригрупповой дисперсиям, не скорректированным на число степеней свободы, a MS — к тем же дисперсиям с учетом степеней свободы.

Все результаты в табл. 7.3 мы уже получили расчетным путем, за исключением наблюдаемого уровня значимости (/^-значения). Напомним, что /^-значение представляет собой наименьшую вероятность отвергнуть нулевую гипотезу, если она истинна, — совершить ошибку первого рода. В рассматриваемой задаче такая вероятность исчезающе мала — 0,5, что придает нам уверенности в полученных результатах.

В заключение назовем основные требования к данным, которые являются условиями адекватного применения дисперсионного анализа:

юо.

• 1. Наблюдения и группы не зависят друг от друга.
• 2. Дисперсия всех совокупностей постоянна (существенно не меняется от одной группы к другой).
• 3. Распределение совокупностей не должно сильно отличаться от нормального.

Донне.ыи Р. Статистика. М., 2006. С. 292—296.

Иванов О.В. Статистика. Учебный курс для социологов и менеджеров. М" 2005. Ч. 2. С. 123−146.

Кремер Н.Ш. Теория вероятностей и математическая статистика. М" 2007. С. 379−395.

Интернет-ресурсы.

Clayton State University, School of business. Electronic Textbook on Business Statistics: ANOVA. http://business.clayton.edu/arjomand/book/ sbk27.htm.

• [1] Рисунок взят с сайта https://onlinecourses.science.psu.edu/.