Упрощения при расчете рам на устойчивость

Для целого ряда расчетных схем использование метода перемещений в расчетах на устойчивость в общем виде является нецелесообразным из-за сложности получаемых уравнений устойчивости. В таких случаях используются те же приемы упрощения решений, что и при решении задач прочности: основная система без постановки линейных связей и учет симметрии.

Основная система без постановки линейных связей. Основная система без постановки линейных связей может быть использована для расчетных схем типа консольной стойки ступенчатого сечения (рис. 16.13, а), когда ничто не препятствует горизонтальному смещению узлов, за которые принимаются места ступенчатого изменения сечений, а поперечные силы во всех сжатых стержнях равны нулю. К указанному типу расчетных схем можно отнести раму (рис. 16.13, б) и статически определимую балку ломаного очертания (рис. 16.13, в).

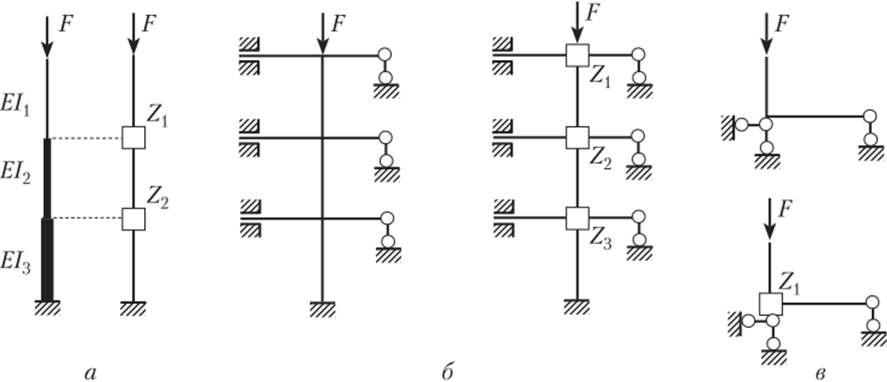
Рис. 16.13.

В приведенных расчетных схемах основную систему получают введением только узловых дополнительных связей («плавающих» заделок), препятствующих только угловым смещениям.

Как и при расчете на прочность, будем иметь дело с двумя дополнительными типами стержней, которые были показаны в подпараграфе 14.3.1 (см. рис. 14.13), но в расчетах на устойчивость они загружены сжимающими силами.

Чтобы воспользоваться основной системой без постановки линейных связей, необходимо знать значения реакций для указанных двух типов стержней. Эти значения получают с помощью непосредственного интегрирования дифференциального уравнения изогнутой оси стержня.

Рассмотрим консольный стержень (рис. 16.14, а), который по своей работе равнозначен стержню, изображенному на рис. 14.13, б_} и зададим единичный угол поворота защемления (рис. 16.14, б).

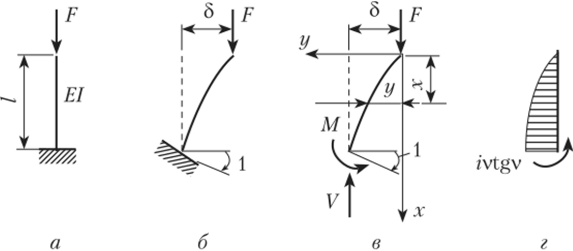
Рис. 16.14.

По полученному для стержня равновесному состоянию (рис. 16.14, в) определим изгибающий момент в произвольном сечении с координатами х и у: М (х) = Fy.

Подставив полученное выражение изгибающего момента в дифференциальное уравнение (10.19), получим.

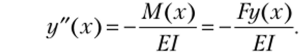
Введя обозначение, а = F_Kp/EI, представим дифференциальное уравнение в канонической форме: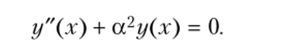

Получаем уже знакомое дифференциальное уравнение с известным решением.

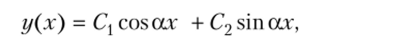
производная которого.

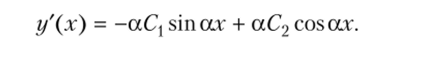
Записав граничные условия для рассматриваемого стержня, получим.

• 1) при х = 0 у = 0, следовательно, С_х = 0;
• 2) при х = 1 у' — 1, следовательно, аС₂ cos а/ = 1, откуда

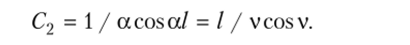
Определив С₂, можем записать уравнение изогнутой оси стержня.

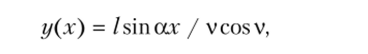
на основании которого определим относительное смещение концов стержня:

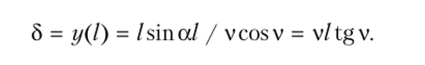
Изгибающий момент в заделке при F= v²EI/l² [см. формулу (16.2)] согласно рис. 16.14, г

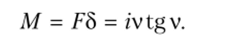
Аналогично получают значения реакций и для второго типа стержня. Выражения для реакций приведены в прил. 12 (и. 5 и 6), а значения специальных функций, входящих в эти выражения — в прил. 14.

Учет симметрии. Рассмотрим симметричную и симметрично загруженную раму (рис. 16.15, а), являющуюся трижды кинематически неопределимой, т. е. при получении основной системы метода перемещений необходимо ввести три дополнительные связи — две угловые и одну линейную. В силу симметрии расчетной схемы можно воспользоваться способом группировки неизвестных для симметрично расположенных неизвестных. Соответственно, рассмотрим три вспомогательных состояния от принудительного смещения связей.

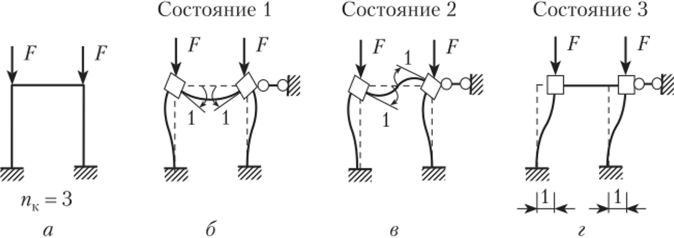
Рис. 16.15.

В силу симметрии побочные коэффициенты r₁₂ = r₂₁ ⁼ Пз ^{= Г}31 ⁼ О, в результате чего общий определитель (16.7) при п_к = 3 распадается на два определителя:

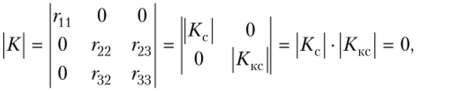
что позволяет рассматривать отдельно |/С_с| = 0 и К_кс = 0.

Таким образом, при определении устойчивости симметричных и симметрично загруженных рам упрощение расчета сводится к отдельному рассмотрению симметричной и кососимметричной форм потери устойчивости.

Рассмотрим формы потери устойчивости (рис. 16.16, а) для имеющих одинаковые геометрические размеры несвободной (не имеющей горизонтальных смещений ригеля) и свободной (ригель имеет горизонтальные смещения) рам. Нетрудно заметить, что симметричная форма потери устойчивости у этих рам (рис. 16.16, б) одинакова, а кососимметричные формы (рис. 16.16, в) разнятся, и существенно.

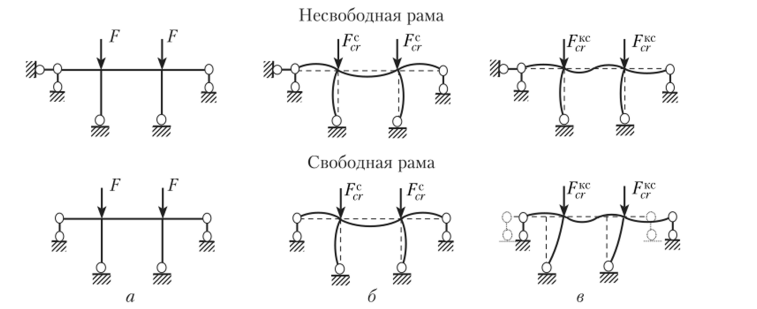
Рис. 16.16.

Приведенные формы потери устойчивости позволяют сделать выводы, доказанные инженерной практикой:

• • для несвободных рам F?_r < F™;
• • для свободных рам F*^c < F₍⁽_r.

Так же как и при решении задач прочности, расчетную схему при выбранной форме потери устойчивости можно представить в виде ее симметричной части.

На рис. 16.17 рассмотрены симметричная несвободная рама и расчетные схемы ее симметричной части для обеих форм потери устойчивости. Степень кинематической неопределимости рамы п_к = 2. Для симметричной формы потери устойчивости (рис. 16.17, а) имеем п_к = 1, для кососимметричной формы (рис. 16.17, б) — также п_к = 1.

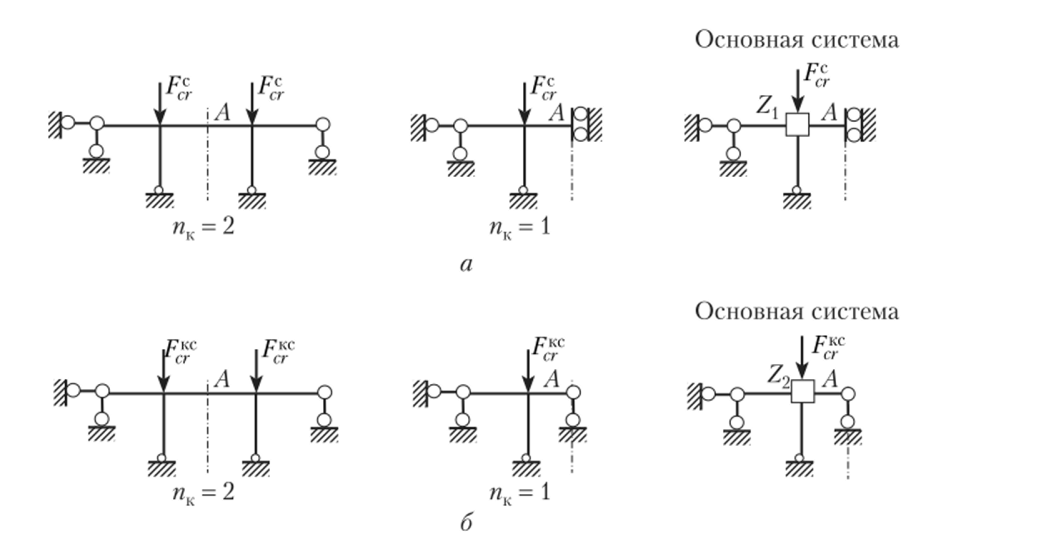
Рис. 16.17.

По аналогии для свободной рамы (рис. 16.18) при п_к = 3 имеем: для симметричной формы потери устойчивости (рис. 16.18, а) п_к = 1; для кососимметричной формы (рис. 16.18, 6) п_к = 1. Общее число уравнений меньше трех, так как при рассмотрении кососимметричной формы возможно использование основной системы без постановки линейной связи.

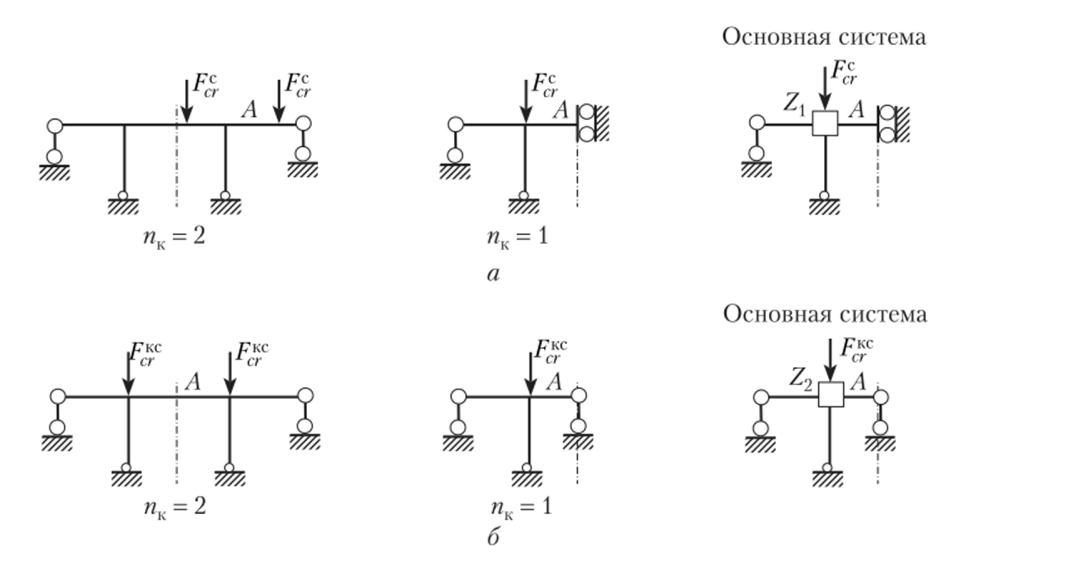
Рис. 16.18.

Пример 16.7

Требуется определить наименьшее значение критической силы для симметричной расчетной схемы, показанной на рис. 16.19, а.

Рис. 16.19.

Относительные жесткости стержней схемы, приведенные к единому множителю:

• — стоек ij = El / 1 = i;
• — ригеля i₂ = 2El / l = 2i.

Решение. 1. Расчетная схема имеет несмещаемый по горизонтали ригель, следовательно, наименьшей будет критическая сила при симметричной форме потери устойчивости (рис. 16.19, б).

• 2. Представим расчетную схему в виде ее симметричной части, которая имеет один жесткий узел, закрепленный от горизонтальных и вертикальных смещений (рис. 16.19, в). Следовательно, п_к = 1.
• 3. Уравнение устойчивости на основании (16.7) при п_к = 1 имеет вид г_п = 0.
• 4. Основная система, полученная введением одной угловой связи, показана на рис. 16.19, г.
• 5. Зададим введенной дополнительной связи принудительное единичное смещения (угол поворота), покажем деформированную схему основной системы от этого смещения (рис. 16.19, д) и построим в основной системе эпюру М,° (рис. 16.19, ё). При этом для ригеля схемы, не испытывающего влияния сжимающих сил, эпюру изгибающих моментов строим по табл. 6 прил. 10, а для сжатой вертикальной стойки — по табл. 5 прил. 12.
• 6. Реакция в дополнительной связи из условия равновесия r_n = -ivtgv+4i.
• 7. Подставляя значение г, _t в уравнение устойчивости, получим уравнение vtgv = 4, решение которого по прил. 14: v = 1,26.

Величина критической силы согласно формуле (16.2) F_cr = 1,26²Е1 / Р = 1,59El/1², а расчетная длина стержня согласно формуле (16.5) /₀ = (к / 1,26)/ = 2,49/.

Пример 16.8.

Требуется определить критическую силу и расчетные длины сжатых стоек для симметричной рамы, показанной на рис. 16.20, а. Рама имеет один абсолютно жесткий ригель. Для всех остальных стержней El — const.

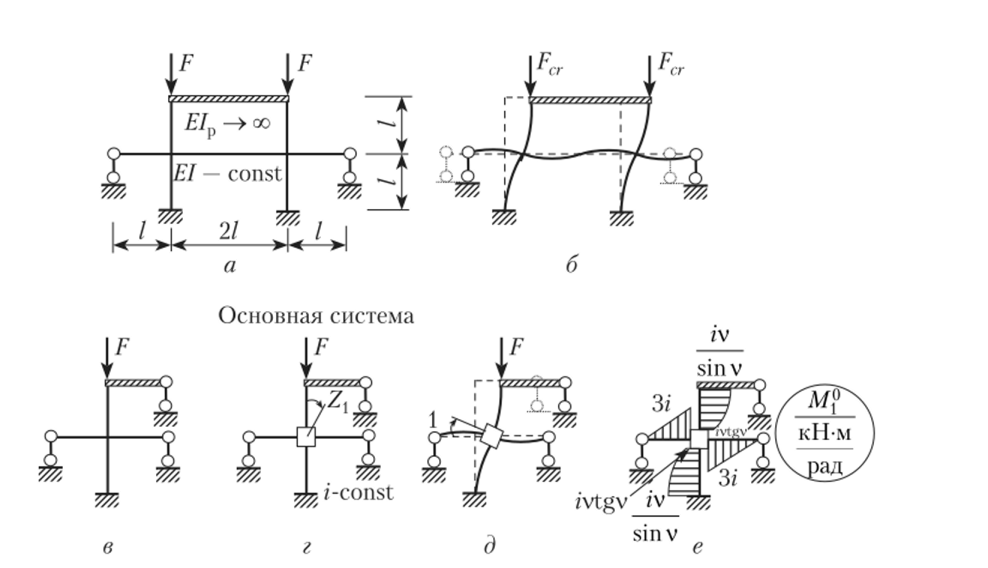
Рис. 16.20.

Для сжатых стоек рамы при одинаковых длинах, жесткости и сжимающей силе величина критического параметра v-const.

Решение. 1. Ригели рамы способны смещаться по горизонтали, т. е. рама является свободной. Следовательно, наименьшей будет критическая сила при кососимметричной форме потери устойчивости (рис. 16.20, 6).

• 2. Представим расчетную схему в виде ее симметричной части (рис. 16.20, в), которая имеет один жесткий узел, способный к повороту. Поперечные силы в сжимаемых стойках равны нулю, поэтому для полученной схемы можно использовать основную систему без постановки линейных связей. Следовательно, п_к= 1.
• 3. Уравнение устойчивости на основании (16.7) при п_к = 1 имеет вид г_п = 0.
• 4. Основная система, полученная введением одной угловой связи, показана на рис. 16.20, г.
• 5. Задаем введенной дополнительной связи принудительное единичное смещение (угол поворота), показываем деформированную схему основной системы от этого смещения (рис. 16.20, д) и строим в основной системе эпюру М{* (рис. 16.20, е). При этом для ригеля схемы, не испытывающего влияния сжимающих сил, эпюру изгибающих моментов строим по прил. 10, а для сжатой вертикальной стойки — по прил. 12.
• 6. Реакция в дополнительной связи из условия равновесия г_{{ {} = 2iv / tgv + 6/.
• 7. Подставляя значение г_п в уравнение устойчивости, получим уравнение v / tgv = = -3, решение которого по прил. 14: v = 2,45.

Критическая сила согласно формуле (16.2) F_cr= 2,45²?7 / Р = 6,00/f/ / Р, а расчетная длина стержня согласно формуле (16.5) /₀ = (тс / 2,45)/ = 1,28/.