Сигналы с угловой модуляцией

Обратимся к аналоговым модулированным сигналам, полученным путем изменения по закону передаваемого сообщения в несущем колебании (2.63) частоты со₀ или начальной фазы (р₍₎. Поскольку в этих случаях происходит линейное влияние на аргумент косинуса, а сам аргумент гармонического колебания = со₀t + ср₍₎ определяет мгновенное значение фазы, такие сигналы называют сигналами с угловой модуляцией (УМ). Если в несущем колебании изменяется частота со₀, то имеем дело с частотной модуляцией (ЧМ), если же изменяется начальная фаза ср₀ — то с фазовой модуляцией (ФМ). По существу различие между фазовой и частотной модуляцией заключается лишь в том, как именно мгновенная фаза ц/(?) связана с модулирующим сигналом. Чтобы оценить связь частотной модуляции с фазовой, введем понятие мгновенной модуляции, равной производной от полной фазы по времени со (?) = dj/dt.

Частотная модуляция. Начало широкого практического применения ЧМ в радиовещании положил в 1935 г. Э. Армстронг^[1].

При частотной модуляции (frequency modulation — FM) мгновенное значение несущей частоты со(t) связано с модулирующим сигналом e (t) зависимостью.

где &_ч — размерный коэффициент пропорционачьности между частотой и напряжением, радДВс).

Рассмотрим однотопальпую частотную модуляцию, когда модулирующий сигнал — гармоническое колебание e (t) = E_{)cosQt, у которого для упрощения начальная фаза 0₍₎ = 0. Пусть и начачьная фаза несущего колебания ф₍₎ = 0. При необходимости начальные фазы (р₍₎ и 0₍₎ легко можно ввести в окончательные соотношения. Полную фазу ЧМ-сигнала в любой момент времени t определим путем интегрирования мгновенной частоты (2.79):

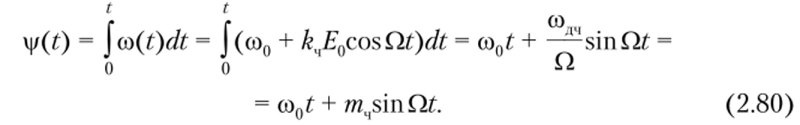
В формуле (2.80) со_дч = k_ч?₀ — максимачьное отклонение частоты от значения со₀, или девиация частоты {frequency deviation) при частотной модуляции; т_ч = со_лч/П = k_X]E₀/Q — максимальное отклонение от текущей фазы со₀?, или девиация фазы несущего колебания, которая называется индексом частотной модуляции. Данный парамер определяет интенсивность колебаний начальной фазы радиосигнала.

С учетом соотношений (2.63) и (2.80) частотно-модулированный сигнал запишется в следующем виде:

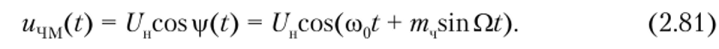
На рис. 2.36 представлены упрощенные временные диаграммы сигналов при частотной модуляции. Несущее колебание u_n{t) с начальной фазой 0_О = = 90° показано па рис. 2.36, а, модулирующий сигнал e (t) с начальной фазой Ф₀ = 90° — на рис. 2.36, б и полученный в процессе частотной модуляции ЧМ-сигнал и_чм(?) — на рис. 2.36, в. Нетрудно заметить, что по форме временная диаграмма ЧМ-сигнала напоминает сжатые и растянутые меха русской гармошки. Форма и уровень сжатия или растягивания несущего колебания зависят от значения индекса частотной модуляции т_г

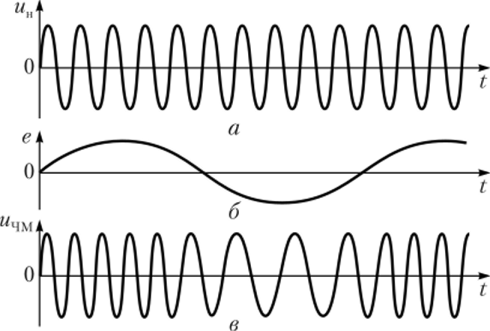
Рис. 2.36. Частотная однотональная модуляция:

а — несущее колебание; б — модулирующий сигнал; в — ЧМ-сигиал.

Спектр ЧМ-сигнала при однотональной модуляции. Используя известные тригонометрические преобразования, запишем формулу (2.81) следующим образом (здесь и далее индекс у коэффициента модуляции т_ч опущен, т. е. т_к{ = т)

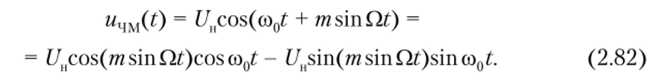
Проанализируем выражение (2.82) отдельно для малых (т 1) и больших (т > 1) индексов модуляции.

Спектр ЧМ-сигнала при т 1. Такую угловую модуляцию называют узкополосной. В этом случае имеют место приближенные равенства

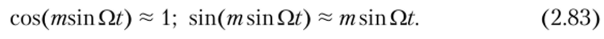
Подставив равенства (2.83) в формулу (2.82), после несложных преобразований получим (при начальных фазах модулирующего и несущего колебаний 0_О = 0 и ф₀ = 0).

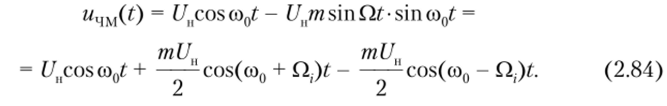
Сравнение формул (2.84) и (2.69) показывает, что по аналитической записи спектр ЧМ-сигнала при однотональной модуляции напоминает спектр AM-сигнала и также состоит из несущего колебания и двух боковых составляющих с частотами (со₀ + Q) и (со₀ — Q), причем и их амплитуды рассчитываются аналогично (только вместо коэффициента амплитудной модуляции М в формуле для ЧМ-сигнала фигурирует индекс угловой модуляции т). Но есть и принципиальное отличие, превращающее амплитудную модуляцию в частотную: знак «минус» перед одной из боковых составляющих.

На рис. 2.37, а показана спектральная диаграмма для однотоналыюго ЧМ-сигнала при индексе модуляции т 1. Отметим очевидное: ширина спектра ЧМ-сигнала, как и спектра AM-сигнала, равна 2Q.

Построим векторную диаграмму ЧМ-сигнала аналогично тому, как это было сделано для однотоналыюй амплитудной модуляции (рис. 2.37, б).

На диаграмме показано, как поворот фазы вектора AD нижней боковой составляющей U_HB на 180° влияет на вектор результирующего колебания 05, который изменяет свое направление относительно вектора несущей.

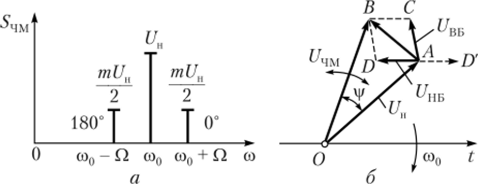
Рис. 237. Диаграммы ЧМ-сигнала при т <�ЗС 1:

а — спектральная; б — векторная.

ОА. Такое изменение направления вектора ОБ характерно для угловой модуляции и это отличает ее от амплитудной. В то же время изменение направления вектора AD на 180° не влияет на вектор модуляции АВ, который всегда перпендикулярен вектору несущей ОА (для сравнения направление вектора AD нижней боковой составляющей при AM-сигнале обозначено штриховой линией — вектор AD'). Итак, вектор результирующего ЧМ-колебания ОБ изменяется по фазе, т. е. с течением времени «качается» вокруг центрального положения. При этом вектор изменяется и по амплитуде, хотя теоретически этого не должно быть. Этот нюанс связан с тем, что формула (2.84) является приближенной, поскольку равенства (2.83) имеют приближенный характер. Однако при т 1 изменения амплитуды вектора результирующего колебания ОБ настолько малы, что ими можно пренебречь и модуляцию рассматривать как частотную.

Спектр ЧМ-сигнала при т > 1. Этот случай представляет основной практический интерес, поскольку при больших т помехоустойчивость передачи сигнала существенно выше, чем при амплитудной модуляции. Здесь при расчетах оказывается удобным аппарат функций Бесселя^[2]. Из математики известно, что эти функции косвенно определяются следующим образом:

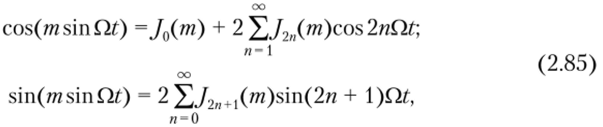
гдеJ_tl(nг) — функция Бесселя 1-го рода п-го порядка.

В теории функций Бесселя доказывается, что функции с положительными и отрицательными индексами связаны между собой формулой.

Ряды (2.85) подставим в формулу (2.82) и заменим произведение косинусов и синусов полусуммами косинусов нужных аргументов. Тогда, с учетом формулы (2.86).

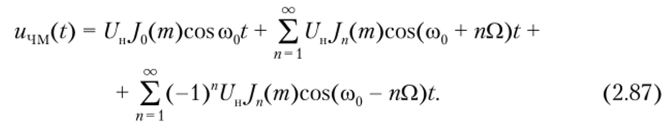
Спектр ЧМ-сигнала с однотоналыюй модуляцией при т > 1 состоит из множества гармоник: несущего колебания и бесконечного числа боковых составляющих с частотами со₀ + пЛ и со₀ — пЛ, расположенных попарно и симметрично относительно несущей со₀. Исходя из выражения (2.87) можно отметить, что начальные фазы боковых колебаний с частотами со₀ + пЛ и со₀ — пЛ совпадают, если п — четное число, и отличаются на 180°, если п — нечетное.

Теоретически спектр ЧМ-сигнала (также и ФМ-сигнала) бесконечен, однако в реальных случаях он ограничен. Для детального анализа и построения спектральных диаграмм необходимо знать поведение функций J_rl(m) при различных т в зависимости от п.

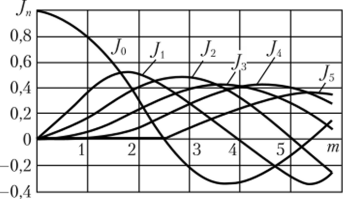
Рис. 2.38. Графики функций Бесселя.

На рис. 2.38 показаны графики ряда функций Бесселя. Отметим, что чем больше индекс функции Бесселя, тем протяженнее область аргументов, при которых функция мала. Поэтому считают, что начиная с номера п > т + 1 значения функций Бесселя становятся весьма малыми и практическая ширина спектра сигналов с угловой модуляцией.

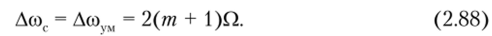
ЧМи ФМ-сигналы, применяемые на практике, имеют т > 1, поэтому.

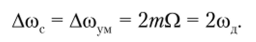
Полоса частот ЧМ-сигнала с однотональной модуляцией равна удвоенной девиации частоты и не зависит от частоты модуляции. Спектр ЧМ-сигнала с угловой модуляцией при негармоническом модулирующем сигнале определить трудно. Но он всегда сложнее, чем спектр AM-сигнала при том же модулирующем сигнале. Спектр простейшего ЧМ-сигнала при т = 3 показан на рис. 2.39.

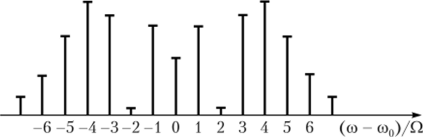
Рис. 2.39. Спектр простейшего ЧМ-сигнала.

Фазовая модуляция. В ФМ-сигнале полная фаза несущего колебания изменяется пропорционально модулирующему сигналу:

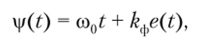
где Аф — размерный коэффициент пропорциональности, рад/В.

При однотональной модуляции фаза несущего колебания.

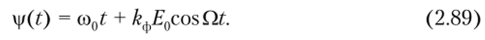
Из формулы (2.89) следует, что, как и в случае частотной модуляции, полная фаза несущего колебания при фазовой модуляции изменяется по гармоническому закону. Максимальное отклонение фазы несущего колебания от начальной фазы характеризует индекс фазовой модуляции

Подставляя выражения (2.89) и (2.90) в соотношение для несущей (2.63), получим.

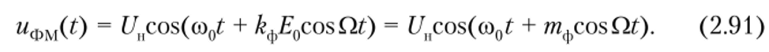
Дифференцируя формулу (2.89), находим мгновенную частоту ФМ-сигнала:

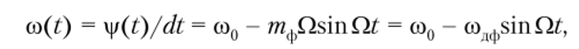
где со_дф = т_(])П = E₀Q — максимальное отклонение частоты от значения несущей со₀, т. е. девиация частоты при фазовой модуляции.

Пример 2.6.

ФМ-сигнал амплитудой U_H = 5 В и несущей частотой/₀ = 200 МГц модулирован однотональным гармоническим колебанием с частотой F— 20 кГц при индексе модуляции т = 10. Запишем выражение для ФМ-сигнала, определим пределы, в которых изменяется частота, и рассчитаем ширину спектра.

Решение

Воспользовавшись формулой (2.91), запишем ФМ-сигнал:

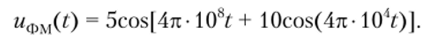
Определим девиацию циклической частоты:

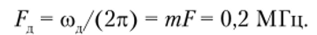
Значит, при фазовой модуляции мгновенная частота изменяется в пределах.

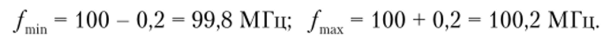
Ширина спектра ФМ-сигнала по формуле (2.88) будет.

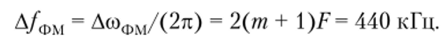
В сводной табл. 2.2 показано, как связаны с модулирующим однотональным сигналом различные характеристики модулированного колебания при фазовой и частотной модуляции. Наглядное представление о законах изменения частоты и фазы при частотной и фазовой однотональной модуляции дают графические построения колебаний, представленные на рис. 2.40.

Выражения (2.84), (2.91) и приведенные на рис. 2.40 соответствующие им графики показывают, что при однотональной угловой модуляции невозможно определить, является ли сигнал частотноили фазомодулированным. Различия между этими достаточно близкими видами угловой модуляции проявляются только при изменении значений амплитуды Е₀ или.

Таблица 2.2

Сигналы с угловой модуляцией.

Закон модуляции.	e (t) = ?0cosQ?
Вид сигнала.	ЧМ.	ФМ.
Аналитическая запись.
Изменение частоты.
Девиация частоты.
Индекс модуляции.
Отклонение фазы.

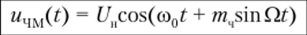
Рис. 2.40. Графики изменения частоты и фазы при угловой однотональной модуляции:

а, 6 — модулирующий сигнал; в, г — частота; д, е — фаза частоты Q модулирующего сигнала e (t). При частотной модуляции девиация частоты со_дч пропорциональна амплитуде Е₀ и не зависит от частоты Q модулирующего сигнала. Индекс же модуляции т_ч прямо пропорционален амплитуде Е₀ и обратно пропорционален частоте Q модулирующего сигнала. При фазовой модуляции девиация частоты со_дф изменяется пропорционально амплитуде и частоте модулирующего сигнала. Индекс модуляции т_ф пропорционален амплитуде Е₀ и не зависит от частоты Q модулирующего сигнала.

Из проведенного анализа данных сигналов можно сделать два вывода:

• • если пропустить модулирующий сигнал через идеальное дифференцирующее устройство, а затем подать его на частотный модулятор, получится сигнал с фазовой модуляцией (верхняя ветвь на рис. 2.41);
• • если пропустить модулирующий сигнал через идеальный интегратор и подать его на фазовый модулятор, получим ЧМ-сигнал (нижняя ветвь на рис. 2.41).

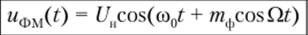
Рис. 2.41. Формирование сигналов с угловой модуляцией

• [1] Эдвин Армстронг (Е. Armstrong, 1890—1954) — американский изобретатель и инженер-электрик, внесший фундаментальный вклад в развитие радио.
• [2] Фридрих Бессель (Е Bessel, 1784—1846) — немецкий математик и астроном.