Теория сборки разнородных модулей

Метод сборки модулей в новые программные системы сложной структуры разработан Е. М. Лаврищевой и В. Н. Грищенко [5−7]. Метод включает в себя математические формализмы определения связей (по данным и по управлению) между объектами сборки и генерации интерфейсных модулей для каждой пары объединяемых модулей. Связь или сопряжение модулей задается оператором вызова CALL, RMI, в котором представлены фактические параметры вызываемому модулю.

Сущность задачи сборки пары разноязычных модулей состоит в определении взаимно однозначного соответствия между задаваемым множеством фактических параметров V = {v_b v₂ v_K} вызывающего модуля и соответствующим множеством формальных параметров F = {f, fi, вызываемого модуля, а также в отображении типов данных одних параметров в другие. Если отображение не удается выполнить, то задача автоматизированной связи для данной пары модулей считается неразрешимой.

Преобразование типов данных осуществляется путем построения алгебраических систем, содержащих для каждого типа множество значений и операций над ними. Каждой операции преобразования типов данных соответствует изоморфное отображение одной алгебраической системы в другую.

Алгебраические системы построены в классе простых типов данных ЯП (/ = b (bool), с (char), i (ini), г (real)), сложных типов данных (I = a (array), z (record), и (union), е (епит)) и допустимых видов их преобразования. Преобразования между типами массивов и записей сводятся к определению изоморфизма между основными множествами соответствующих алгебраических систем с помощью операций изменения уровня структурирования данных — селектора и конструирования. Для массива операция селектора сводится к отображению множества индексов на множество значений элементов массива. Аналогично такая операция определяется для записи как отображение между селекторами компонентов и самими компонентами.

Формально преобразование Р неэквивалентных типов данных в ЯП выполняется следующими этапами.

Этап 1. Построение операций преобразования типов данных Т = {Т_а‘} для множества языков программирования L = { /" }_a=i,".

Этап 2. Построение отображения простых типов данных для каждой пары взаимодействующих компонентов в 1_и и /"2 и применение операций селектора S и конструктора С для отображения сложных структур данных в этих языках.

Формализованное преобразование типов данных осуществляется с помощью алгебраических систем для каждого типа данных Т₍₁‘:

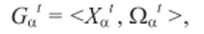
где t — тип данных; Х_а' — множество значений, которые могут принимать переменные этого типа; Q_a'- множество операций над этими типами данных.

Простым и сложным типам данных современных ЯП соответствуют классы алгебраических систем:

Каждый элемент класса простых и сложных типов данных определяется на множестве их значений и операций над ними:

где t = Ь, с, i, г, a, z, и, е.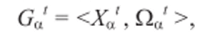

Операциям преобразования каждого t типа данных соответствует изоморфное отображение двух алгебраических систем с совместимыми типами данных двух разных ЯП. В классе систем Х| и Х₂ преобразование типов данных /-> q для пары языков /, и 1_Ч обладает такими свойствами отображений:

• 1) GJ и Gp⁴ — изоморфны (<7 определенный на том множестве, что и /);
• 2) между Ха и Хр⁴ существует изоморфизм, для которых множества С2_а‘ и Ор⁹ разные. Если Г2 = Q"' п Пр*⁷ не пусто, то рассматриваем изоморфизм между G «''= < X_tt', Q > и Gp¹⁷ =. Такое преобразование сводится к случаю 1;

Между множествами Х_а^! и Хр⁴ может не существовать изоморфного соответствия. В этом случае необходимо построить такое отображение между XJ и Хр, чтобы оно было изоморфным. Если такое отображение существует (в каждом конкретном случае оно может быть разным), то имеем условие случая I) с соответствующими изменениями в определении алгебраических систем;

3) мощности алгебраических систем должны быть равны I Gj I = I Gp*1.

Любое отображение 1, 2 сохраняет линейный порядок, так как алгебраические системы (1.1) линейно упорядочены.

Лемма 1. Для любого изоморфного отображения <�р между алгебраическими системами Ga И Gp* ВЫПОЛНЯЮТСЯ равенства ф (Xd . min) = Xf. min, ф (Ха¹. max) = Xf?^

Доказательство леммы тривиальное и простое. При условии, когда одно или два вышеприведенных равенства не выполняются, тогда для основных множеств алгебраических систем изменяется линейный порядок, что противоречит определению.

Формальные условия преобразования типов данных / = с b, г, а, z определяются теоремами 1 — 5 [5−7].

Теорема 1. Пусть ф — отображение алгебраической системы G_a^c в систему Gp^c. Для того, чтобы ф было изоморфизмом, необходимо и достаточно, чтобы ф изоморфно отображало Х_а^с на Хр с сохранением линейного порядка.

Необходимость. Пусть (р — изоморфизм. Тогда при отображении сохраняются все операции множества С2 = С1_а^с = Пр^с, в том числе и операция отношения, которая определяет линейный порядок Х_а^с и Хр

Достаточность. Пусть (р изоморфно отображает Х_а^с на Хр с сохранением линейного порядка. Операция отношения выполняется соответственно принципу упорядоченности. Операцию succ докажем с помощью леммы, согласно которой выполняется равенство ф (Х_а^с _mi_n)⁼ Хр. _mi_n;

Последовательно применяя операцию succ к этому равенству и учитывая линейную упорядоченность Х_и^с и Х^ср (х< succ (x)), получаем, что для любого х^с_а е Ха и х^с_а * Xd _min из равенства ф {Х^) = ]?р, где х^сре Хр, выполняется равенство.

Операция pred доказывается аналогично с помощью ф (Х_а^с «*, 0 = Хр^с _х.

Теорема 2. Любой изоморфизм (р между алгебраическими системами G_a^b и Gp^b является тождественным изоморфизмом:

Доказательство. При отображении G_a^b и Gp всегда справедливо Х_а, ыж < Хр aJ⁷. Поэтому, учитывая сохранение линейного порядка, единственно возможным изоморфизмом является (3).

Теорема 3. Любой изоморфизм между алгебраическими системами с соответствующими числовыми типами является тождественным автоморфизмом.

Доказательство этой теоремы тривиальное и является следствием свойств элементов числовых множеств.

Теорема 4. Пусть G_a" и Gp" - алгебраические системы, которые отвечают типам данных массива (а); <�р, и.

v — изоморфные отображения множеств индексов (/) и значений элементов (У) массивов, которые сохраняют линейный порядок. Тогда изоморфизм (р между алгебраическими системами целиком определяется изоморфными отображениями:

Изоморфизм <�р между алгебраическими 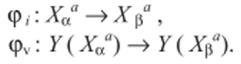системами G_a" и Gp" определяется отображениями (р< и.

v, которые сохраняют линейный порядок и упорядоченность элементов массива.

Теорема 5. Пусть G_a^: и Gp^z — две алгебраические системы, которые отвечают типам данных «запись» или структура и х_а^г € Х_а^:, х$ е Х$. Тогда, если между последовательностями компонентов записей х_а^: и, vp‘ существует взаимно однозначное соо тветствие, то изоморфизм <�р между Gd и Gp' определяется изоморфными отображениями алгебраических систем, которым соответствуют компоненты записи или структуры.

Преобразования между массивами и записями сводятся к преобразованию простых типов данных их элементов. Преобразования между действительными типами и другими числовыми значениями предполагают использование эмпирических случаев, так как отсутствует изоморфизм основных множеств этих алгебраических систем.

При преобразовании простых и структурных типов используются операции селектора S и конструирования С для изменения уровня структурирования данных. Операция селектора S для массива определяется в виде ограничения отображения: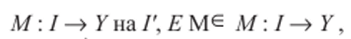

где Е — вложения /'^е /. Тогда МI {к} соответствует к — элемент массива при Г = {А). Аналогично эта операция определяется и для записи М I {S_lw}, где М — отображение между селекторами компонентов и самими компонентами, a S_vm определяет соответствующий компонент записи.

Операция конструирования С массива состоит в формальном приведении в порядок компонентов и определении соответствия между множеством индексов и множеством элементов массива. Аналогично эта операция определяется для записи.

Таким образом, множество операций Р, S и С определяет элементарные правила для конструирования сложных типов данных из более простых для взаимодействующих компонентов на разных МП.