Методика решения нормальных уравнений

Последнее уравнение «треугольной» системы должно содержать лишь одно неизвестное (), предпоследнее — два () и т. д. Решение полученной системы уравнений осуществляется последовательным («снизу-вверх») определением из последнего уравнения «треугольной» системы, из предпоследнего и т. д. Применительно к системе уравнений (2.6) преобразование к «треугольному» виду осуществляется за (m — 1) шагов… Читать ещё >
Методика решения нормальных уравнений (реферат, курсовая, диплом, контрольная)
Уравнения (2.7) представляют собой систему линейных алгебраических уравнений, где квадратная матрица A называется матрицей системы, вектор C — вектором-столбцом неизвестных системы, а вектор B — вектором-столбцом свободных членов.

(2.8).
Решение системы линейных уравнений сводится к отысканию значений элементов вектора-столбца С, называемых корнями системы. для получения единственного решения системы, входящие в нее m уравнений должны быть линейно независимыми. необходимым и достаточным условием этого является неравенство нулю определителя данной системы, то есть detA? 0.
Один из возможных способов минимизации критерия аппроксимации (2.2) предполагает решение системы нормальных уравнений (2.6). При выборе в качестве аппроксимирующей функции линейной функции искомых параметров нормальные уравнения представляют собой систему линейных алгебраических уравнений.
Методика вычислений методом Гаусса
Одним из наиболее широко используемых прямых методов является метод последовательного исключения неизвестных, или метод Гаусса. Согласно этому методу, исходная система линейных уравнений (2.6) преобразуется путем последовательного исключения неизвестных в эквивалентную систему уравнений, имеющую так называемый «треугольный» вид.
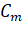
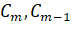
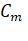
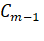
Последнее уравнение «треугольной» системы должно содержать лишь одно неизвестное (), предпоследнее — два () и т. д. Решение полученной системы уравнений осуществляется последовательным («снизу-вверх») определением из последнего уравнения «треугольной» системы, из предпоследнего и т. д. Применительно к системе уравнений (2.6) преобразование к «треугольному» виду осуществляется за (m — 1) шагов.
Процедура описанного выше преобразования будет следующая:


На первом шаге выделяется первое уравнение системы (2.6). Это уравнение не преобразуется, и оно объявляется ведущим уравнением. Затем исключается неизвестноеиз второго уравнения. Для этого ведущее уравнение умножается на коэффициент и вычитается из второго уравнения. В результате получим следующее уравнение:
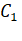
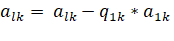
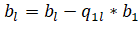
Очевидно, что коэффициент при равен нулю. Аналогичную процедуру можно проделать с третьим уравнением системы. Для исключенияиз m-го уравнения необходимо умножить ведущее уравнение на и вычесть результат из m-го уравнения. Вводя новые обозначения для коэффициентов и свободного члена, можно представить систему уравнений (2.6) в виде (2.9).
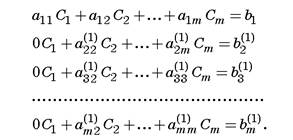
(2.9).
Эту последовательность действий необходимо повторять до тех пор, пока матрица (2.9) не примет треугольный вид (2.10).

(2.10).
Этот процесс называется прямым методом Гаусса. А решение этой треугольной системы обратным методом Гаусса. Общая формула вычислений имеет вид (2.11):
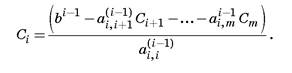
(2.11).
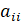
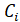
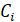
В процессе прямого хода метода Гаусса может оказаться, что коэффициент ведущего уравнения равен нулю. Тогда исключить из остальных уравнений рассмотренным методом нельзя. Однако уравнения системы можно поменять местами и объявить ведущим то уравнение, у которого коэффициент при неизвестном отличен от нуля. Отметим, что системы, отличающиеся лишь взаимным расположением образующих их уравнений, являются эквивалентными. Перестановка уравнений не только допустима, но часто и полезна для уменьшения погрешности арифметических вычислений. Для уменьшения погрешности вычислений в качестве ведущего обычно выбирается уравнение с максимальным по модулю коэффициентом при. Это уравнение и уравнение с номером i меняют местами, и процесс исключения продолжается обычным образом. Поиск максимального по модулю коэффициента при носит название определение ведущего элемента.