Парная регрессия на основе метода наименьших квадратов и метода группировок

Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и при котором минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии: В уравнении регрессии параметр а0 показывает… Читать ещё >
Парная регрессия на основе метода наименьших квадратов и метода группировок (реферат, курсовая, диплом, контрольная)
Парная регрессия позволяет получить аналитическое выражение связи между двумя признаками: результативным и факторным, которая может описываться уравнениями следующего вида:
- • прямой (ух = а0 а,*) —
- • гиперболы ^ух = а0 а,-ь^;
- • параболы {ух = а0+ ахх+ а2×2) и т. д.
Определить тип уравнения можно, исследуя зависимость графически. Однако существуют более общие рекомендации, позволяющие определять форму связи, не прибегая к графическому изображению. Если результативный и факторный признаки возрастают одинаково, то это свидетельствует о том, что связь между ними линейная, а при обратной связи — гиперболическая. Если результативный признак увеличивается в арифметической прогрессии, а факторный значительно быстрее, то используется параболическая или степенная регрессия.
Оценка параметров уравнений регрессии осуществляется методом наименьших квадратов, в основе которого лежит предположение о независимости наблюдений исследуемой совокупности и при котором минимизируется сумма квадратов отклонений эмпирических (фактических) значений результативного признака от теоретических, полученных по выбранному уравнению регрессии:
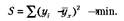
Система нормальных уравнений для нахождения параметров линейной парной регрессии методом наименьших квадратов имеет следующий вид:
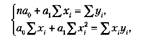
где п — объем исследуемой совокупности (число единиц наблюдения).
В уравнении регрессии параметр а0 показывает усредненное влияние на результативный признак неучтенных в уравнении факторных признаков. Коэффициент регрессии а, показывает, насколько в среднем изменяется значение результативного признака при изменении факторного признака на единицу собственного измерения.
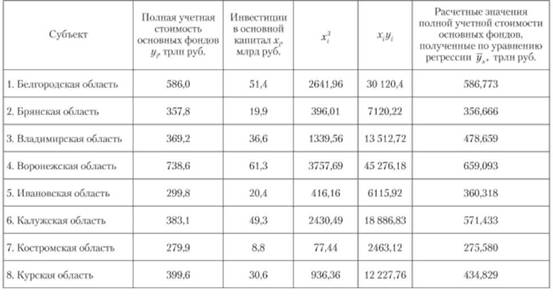
Пример. Имеются следующие данные об инвестициях в основной капитал и полной учетной стоимости основных фондов субъектов Центрального федерального округа РФ в 2010 г. (исключая Москву и Московскую область) (табл. 7.4).
Таблица 7.4. Зависимость между полной учетной стоимостью основных фондов и инвестициями в основной капитал субъектов Центрального федерального округа РФ в 2010 г.
Субъект | Полная учетная стоимость основных фондов трлн руб. | Инвестиции в основной капитал .г., млрд руб. | |||
1. Белгородская область. | 586,0. | 51,4. | |||
2. Брянская область. | 357,8. | 19,9. | |||
3. Владимирская область. | 369,2. | 36.6. | |||
4. Воронежская область. | 738,6. | 61,3. | |||
5. Ивановская область. | 299.8. | 20.1. | |||
6. Калужская область. | 383,1. | 19.: | |||
7. Костромская область. | 279,9. | 8,8. | |||
8. Курская область. | 399,6. | 30,6. | |||
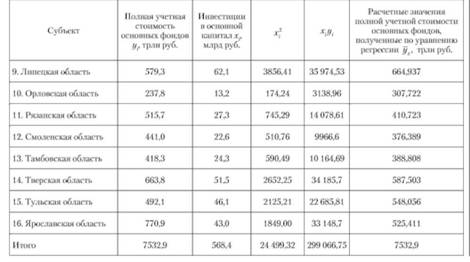
9. Липецкая область. | 579,3. | 62,1. | |||
10. Орловская область. | 237,8. | 13,2. | |||
11. Рязанская область. | 515,7. | 27,3. | |||
12. Смоленская область. | 441,0. | 22,6. | |||
13. Тамбовская область. | 418,3. | 24,3. | |||
14. Тверская область. | 663,8. | 51,5. | |||
15. Тульская область. | 492,1. | 46,1. | |||
16. Ярославская область. | 770,9. | 43,0. | |||
Итого. | 7532,9. | 568,4. | |||
Предположим наличие линейной зависимости между рассматриваемыми признаками.
Построим расчетную таблицу для определения параметров линейного уравнения регрессии полной учетной стоимости основных фондов (табл. 7.5).
Система нормальных уравнений для данного примера имеет вид:
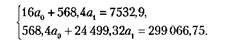
Отсюда а0 = 211,296; в, = 7,305. Следовательно, ух = 211,296 7,305х.+.
Коэффициент регрессии я, = 7,305 означает, что при увеличении инвестиций в основной капитал на 1 млрд руб. полная учетная стоимость основных фондов субъектов Центрального федерального округа возрастет в среднем на 7,305 трлн руб. Подставляя в полученную регрессионную модель фактические значения факторного признака, можно получить расчетные значения результативного признака, приведенные в последней графе табл. 7.5. Если нанести расчетные значения на график, то получится теоретическая линия регрессии, дающая наглядное представление об изучаемой взаимосвязи.
Таблица 7.5. Расчетная таблица для определения параметров уравнения регрессии