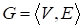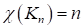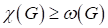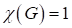Заданы граф, где V — множество вершин; E — множество ребер, и положительное целое число, где — мощность множества V. Раскрасить вершины графа K красками так, чтобы ни одно его ребро не имело соцветных концов. Если такая раскраска невозможна, выдать на экран соответствующее сообщение. Предусмотреть графическое представление исходного графа и цветовое выделение его вершин на экране.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Раскраской вершин графа называется назначение цветов его вершинам. Обычно цвета — это числа 1,2…k. Тогда раскраска является функцией, определенной на множестве вершин графа и принимающей значения во множестве {1,2…k}. Раскраску можно также рассматривать как разбиение множества вершин, где — множество вершин цвета i. Множества называют цветными классами. Раскраска называется правильной, если каждый цветной класс является независимым множеством. Иначе говоря, в правильной раскраске любые две смежные вершины должны иметь разные цвета. Задача о раскраске состоит в нахождении правильной раскраски данного графа G в наименьшее число цветов. Это число называется хроматическим числом графа и обозначается .
В правильной раскраске полного графа все вершины должны иметь разные цвета, поэтому. Если в каком-нибудь графе имеется полный подграф с k вершинами, то для раскраски этого подграфа необходимо k цветов. Отсюда следует, что для любого графа выполняется неравенство .
Однако хроматическое число может быть и строго больше кликового числа. Например, для цикла длины 5, а. Другой пример показан на рис. 1. На нем изображен граф, вершины которого раскрашены в 4 цвета (цвета вершин показаны в скобках). Нетрудно проверить, что трех цветов для правильной раскраски этого графа недостаточно. Следовательно, его хроматическое число равно 4. Очевидно также, что кликовое число этого графа равно 3.
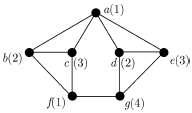
Рис. 1.
Очевидно, что тогда и только тогда, когда G — пустой граф. Нетрудно охарактеризовать и графы с хроматическим числом 2 (точнее, не больше 2). По определению, это такие графы, у которых множество вершин можно разбить на два независимых множества. Но это совпадает с определением двудольного графа. Поэтому двудольные графы называют еще бихроматическими. Согласно теореме Кенига, граф является бихроматическим тогда и только тогда, когда в нем нет циклов нечетной длины.
Для графов с хроматическим числом 3 такого простого описания мы не знаем. Неизвестны и простые алгоритмы, проверяющие, можно ли данный граф раскрасить в 3 цвета. Более того, задача такой проверки (вообще, задача проверки возможности раскрасить граф в k цветов при любом фиксированном) является NP-полной.