Первый достаточный признак

Теорема 2. Пусть G — такой граф, что удаление n вершин породит m несоединенных компонент, таких что m > n + 1, тогда G — негамильтонов.

Доказательство.Предположим противное, пусть исходный граф G — гамильтонов. Если G — гамильтонов, тогда удаление n вершин из G, согласно теореме 1, породит m несоединенных компонент таких что m Ј n + 1. Но это утверждение противоречит условию m > n + 1. Таким образом, предположение оказалось неверно и граф G не может быть гамильтоновым. Теорема доказана.

Пример 3. Продемонстрируем работу теоремы на конкретном примере. Пусть дан граф, изображенный на рисунке 4(a) [2, с. 58].

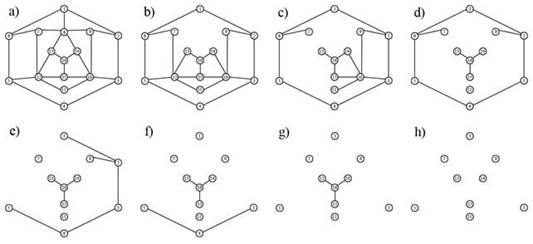
Рисунок 4. Иллюстрация к примеру 3.

Удалим вершину 8. При удалении вершины удаляются и все инцидентные ребра. Получаем граф, изображенный на рисунке 4(b). При удалении несоединенных компонент не появилось. Далее удалим вершину 12. Граф будет иметь вид как на рисунке 4©. Число удаленных вершин n = 2, новые компоненты связности не образовались. Удалим вершину 10, получим ситуацию, изображенную на рисунке 4(d). Образовалось две компоненты связности: {13, 14, 15, 16} и {1, 2, 3, 4, 5, 6, 7, 9, 11}. Получаем n = 3, m = 2. Удалим вершину 6, рисунок 4(e). Теперь стало три компоненты связности: {13, 14, 15, 16}, {7} и {1, 2, 3, 4, 5, 9, 11}. Количество удаленных вершин n = 4, число компонент связности m = 3. Пока условие теоремы не выполняется, продолжаем удаление вершин. Удалим вершину 2, рисунок 4(f). Тогда n = 5, m = 5. Из рисунка видно, что вершины 4 и 16 инцидентны трем ребрам, то есть для появления новых компонент связности целесообразнее было бы удалить одну из них. Удалим вершину 4, получим граф, изображенный на рисунке 4(g). Теперь m = 7, n = 6. Очевидно, что для увеличения компонент связности необходимо удалить вершину 16. После её удаления граф примет вид как на рисунке 4(h). Заметим, что теперь образовалось 9 компонент связности, а количество удаленных вершин равно 7. Таким образом, m = 9, n = 7, 9 > 7 + 1. Получаем, что m > n + 1 удовлетворяет условию теоремы, доказывая, что граф на рисунке 4(a) не содержит гамильтоновой цепи.

Пример 4. Приведем ещё один пример. Пусть дан граф, изображенный на рисунке 5(a). Произведем ту же последовательность действий, как в примере 3.

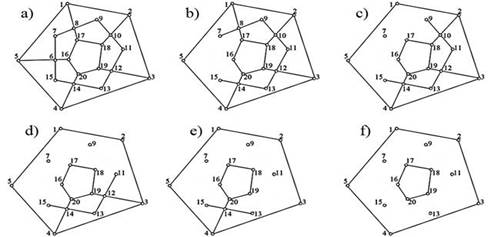
Рисунок 5. Иллюстрация к примеру 4.

На рисунке 4(b-f) показано последовательное удаление вершин 6, 8, 10, 12 и 14. В результате получаем, что число удаленных вершин n = 5, число компонент связности m=7, 7 > 5 + 1. Условие теоремы m > n + 1 выполняется, а это значит, что граф на рисунке 5(a) не содержит гамильтоновой цепи.