Модель переходных вероятностей

Для построения модели зависимости Р₅₅(?), P_SD(t) обратимся к статистике переходных частот, публикуемой Международным рейтинговым агентством, для ключевых рейтинговых разрядов (табл. 8.2 и 8.3).

Таблица 8.2

Одногодовые переходные вероятности (данные 5&Рза 1981—2014 гг.^[1][2][3]), %.

Таблица 83

Двухгодовые переходные вероятности (данные 5&Рза 1981—2014 гг.³), %

Окончание табл. 83

Примечание к табл. 8.2, 83: заголовки строк — это исходный рейтинг; заголовки столбцов — это рейтинг, следующий за исходным. На пересечении указана в ячейке вероятность перехода от исходного к следующему рейтингу.

Используются также трех-, пяти-, семии 10-летние матрицы переходов. Вероятность остаться или повысить рейтинг за определенный период будут оцениваться как сумма вероятностей переходов в более высокий или свой рейтинг.

Для двух рейтинговых уровней ВВ и В строятся вероятности не снижения каждого из этих рейтингов соответственно в зависимости от срока (рис. 8.2).

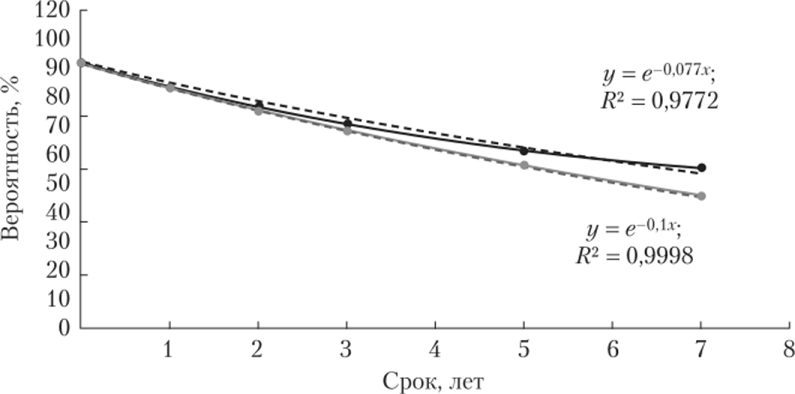
Рис. 8.2. Вероятность отсутствия снижения рейтинга для разрядов В и ВВ:

— ВВ; — В;——экспоненциальная (ВВ);——экспоненциальная (В) Используя результат фиттирования экспоненциальной зависимостью, который показывает отличное качество, можно предложить вполне адекватную и консервативную модель зависимости P$s (t):

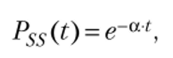
где, а = 0,1.

Фиттирование зависимости вероятности дефолта от времени наиболее эффективно (до срока 5—7 лет) степенной функцией:

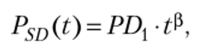
где PDi — среднегодовая вероятность дефолта, а (3— параметр степени, зависящий от рейтинга (вероятности дефолта).

Эту зависимость можно взять за основу модели поведения вероятности дефолта от срока кредитования для практически актуальных сроков (рис. 8.3).

Фиттирование данных S&P зависимости кумулятивного PD от временного горизонта по методу наименьших квадратов дает значения PD_X, р по данным S&P (табл. 8.4).

Таблица 8.4

Оценка параметров вероятности дефолта по данным S&P методом наименьших квадратов.

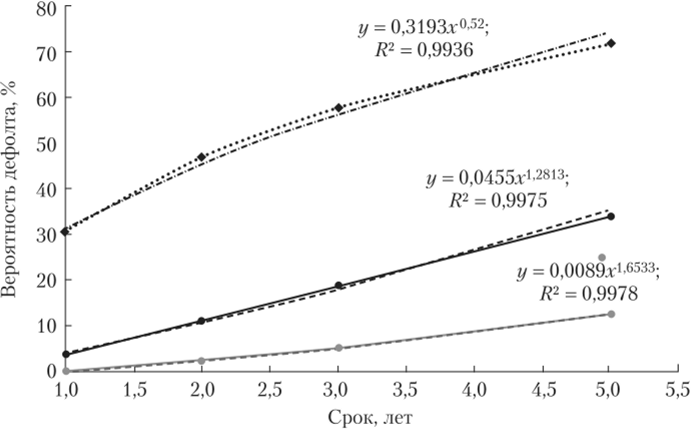
Рис. 8.3. Зависимость вероятности дефолта для сроков кредитования до 5—6 лет для разных риск-классов (данные S&P за 1981—2014 гг.):

• ——В; -•—ВВ; - ССС;
• ——степенная (В);——степенная (ВВ); ———-степенная (ССС)

Для значений PD_X, отличающихся от представленных в табл. 8.4, зависимость (3(РД) можно получить фиттированием по методу наименьших квадратов (зависимость логарифмическая) (рис. 8.4).

Наиболее близкая к статистическим данным зависимость дается формулой (коэффициент детерминации R² = 0,986).

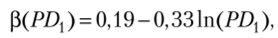
которая позволяет оценить Р(PD) для заданных классов кредитного риска (PD).

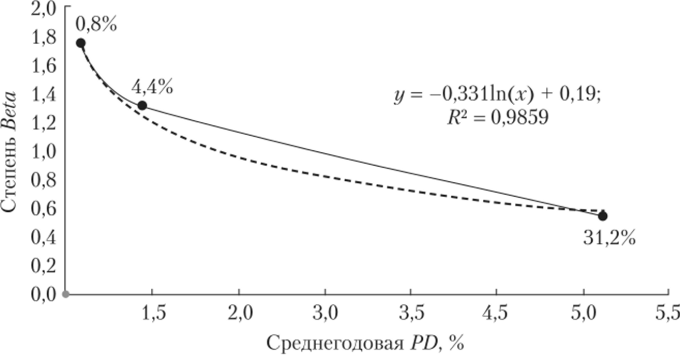
Рис. 8.4. Фиттирование зависимости показателя степени от PD.

Итог: в соответствии с полученными результатами относительно поведения переходных вероятностей для рангов требований кредитоспособности (обратное требование — аппетит к риску дефолта), которые могут считаться приемлемыми для продолжения кредитования клиента при его обращении за ссудой, устанавливаются следующие параметры для зависимостей (табл. 8.5).

Таблица 8.5

Параметры модели зависимости вероятностей от срока

• [1] Погрешность здесь заключается в том, что в расчет идут последующие договоры, одобренные Банком, а не все последующие обращения клиента. Но отклонение Банком последующих обращений имело на практике незначительную долю (не более 10%), что не превышает допустимой погрешности.
• [2] Матрицы преобразованы экстракцией вероятности перехода в состояния NR (No Rated) так, что все вероятности переходов в значимые состояния (AAA — D) равномерно увеличены.
• [3] То же.