Исчисления Айдукевича-Ламбека в S-категориях

Как известно, в 1958 году Дж. Ламбек ввел формальную систему LSC вывода редукций для синтаксических типов [Lambek 1958], которая существенно сильнее классической системы К. Айдукевича, разработанной им еще в 1935 году [Ajdukiewicz 1935].

Согласно В. Бушковскому [Buszkowski 1986], мы можем описать ламбековские синтаксические исчисления (LSC) следующим образом. Зафиксируем счетное множество Рг констант, называемых примитивными типами. Множество Тр (синтаксических) типов будет представлять собой наименьшее, удовлетворяющее следующим условиям:

• (i) Рг с Тр,
• (И) если х, у е Тр, то (х • у), (х /у), (ху)е Тр.

Операционные символы •, /, называются «произведением», «правым» и «левым делением» соответственно. Переменные х, у, z (соотв. /?, q, г соотв. Г; соотв. X, У, Z), с индексами или без индексов, будут пробегать по типам (соотв. примитивным типам; соотв. множествам типов; соотв. конечным последовательностям типов). Любая секвенция вида X -> х (где X * 0) будет называться (редукционной) формулой. Про формулу х -> у будем говорить, что она представляет собой простую формулу. Под сложностью типа формулы будем подразумевать общее число операционных знаков в ней.

Понятие подтипа понимается естественным образом. Под местом подтипа в типе будем подразумевать конкретное вхождение подтипа в тип. Говорят, что множество Т замкнуто, если наряду с каждым типом Т также содержит каждый подтип типа. С1(Т) будет обозначать наименьшее замкнутое множество, содержащее Т.

Переменная R будет пробегать по множествам формул. T® обозначает множество тех типов, которые появляются в некоторых формулах из R, и будем писать Т (Х —> х) вместо Т{Х -> х). Формула X —> х будет называться Г-формулой, если Хе Т, хе Т.

Первая формулировка Ламбека LSC сводилась к системе, чьи формулы являются простыми формулами и чьи аксиомы выглядят следующим образом:

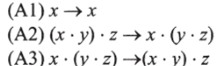
для всех x, y, ze Тр, а выводы выглядят следующим образом:

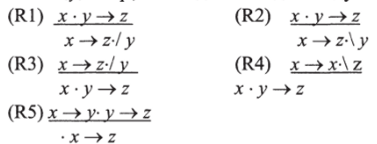
Классические редукционные схемы Айдукевича выглядели следующим образом:

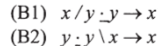
Легко видеть, что эти схемы выводимы в LSC, поэтому нетрудно прийти к выводу, что ламбековское LSC включает в себя систему Айдукевича, будучи существенное сильнее последней.

Секвенциальная формулировка LSC имеет в качестве единственной аксиомы схему (А1), в то время как правила вывода выглядят следующим образом:

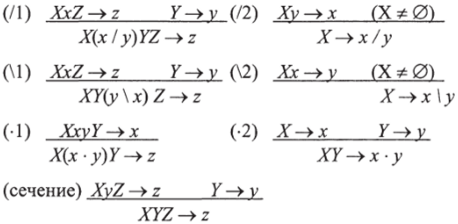
Ламбек в своей работе 1985 г. доказал, что х_ь х₂, … —> х вы водима в данной секвенциальной системе тогда и только тогда, когда, когда х, х₂, … у"~>х (порядок скобок несущественен) доказуема в первой приводимой выше формулировке. Поскольку по;

следняя система фактически является консервативным расширением первой, то будем в дальнейшем отождествлять LSC с последней.

Так называемая S-семантика LSC, представляющаяся наиболее естественной с математической точки зрения, охватывает резидуальные полугруппы, представляющие собой просто структуру М = где представляет собой полугруппу, < есть отношение частичного порядка на I М, а /, являются бинарными операциями на | м, удовлетворяющие следующим тождествам:

(1) для a, b, ce | м, а < с / b тогда и только тогда, когда а b < с тогда и только тогда, когда Ь<�ас.

Если обозначить класс резидуальных полугрупп как RJES, то для каждого М в RES (| М, <, •) является частично упорядоченной полугруппой; это означает, что < выполняет условие монотонности.

(2) для a, b, ce I м если а<�Ь то ac

Для данного М из RES можно стандартным образом расширить оценку v: Рг —>м до интерпретации/ Тр ->|л/| и определить отношение выполнимости:

(3) (A/j/)lh jci, Х2> • • • «*п х тогда и только тогда, когда Л^х) •.

А*т) •… Л*_п) ^А*У

(Л/,/)1Н X —> jc читается как «X -> х значимо в М при fi>. Как обычно, (Mj)-R означает «каждая формула в R значима в М при fi>, а МХ->х (соотв. МR) означает «X -> х (соотв. каждая формула из R) значима в М при каждой оценке v: /V-> | Л/|».

Для данной К с RES говорится, что формула X -" х будет К- значимой, если A/lh X х всякий раз, когда МеК говорится, что формула X —> х будет /^-следствием /?, если Л/lh X —> х всякий раз, когда Me К и v: Рг | м таковы, что A/lh R. Если определить отношение R — X х (читается х выводима из (А1) и формул из R с помощью правил LSC"), то справедлива [Buszkowski 1986, Р-15].

Теорема 1. R УX х тогда и только тогда, когда X —> х является RES-следствием R и следующее.

Следствие. — X —> х тогда и только тогда, когда X —> х является RES-значимой.

Другой семантикой LSC является семантика Дошена GS е RES [Dosen 1988]. Для данной частично упорядоченной полугруппы G = (I G |, <, •) под резидуальной полугруппой над G понимается резидуальная полугруппа М = (IМI, с, ?, /, >, где м состоит из всех А с | G |, таких, что аеА всякий раз как be А и а < b, Q представляет собой включение, а операции определяются следующим образом: для А, В с | G |.

• (4) А? В — {се | G |: с < а? b для некоторых аеА и ЬеВ},
• (5) А / В = {се | G |: с? Ъ е А для каждого ЬеВ},
• (6) АВ = {csg: а ? с е В для каждого аеА}.

GS охватывает все резидуальные полугруппы над частично упорядоченными полугруппами. Приведем еще следующие результаты из [Buszkowski 1986]:

Лемма 1. Каждая М ~ (| м, <, •, /,)е RES может быть изоморфно вложена в резидуальную полугруппу над {| м, <, •).

Следствие, (i) R УX —> х тогда и только тогда, когда X —> х является GS-следствием R.

(ii) I- X —? х тогда и только тогда, когда X —> х является GS-значимой.

Переформулируем S-семантику на языке категории предпорядка.

Определение 1. S-категория представляет собой категорию предпорядка С, снабженную ковариантным бифунктором ®: Су С—> С, таким, что:

• (i) для всяких а.Ь.сеС если существует стрелка а —> Ь, то существуют и стрелки а®с —> Ь®с и с®а —> с®Ь;
• (ii) в С имеются левые => и правые <= экспоненты (резидуалы), т. е. для всяких а.Ь.сеС стрелка а —> с => b существует тогда и только тогда, когда существует а®Ь -> с тогда и только тогда, когда существует b а <= с;
• (iii) ® ассоциативен, т. е. а®(Ь®с)? (а®Ь)®с.

Следующий список представляет собой словарь перевода LSCформул в S-категорию:

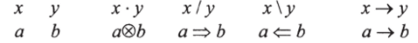
Этот перевод позволяет нам отождествить объекты и стрелки в С и LSC-формулы. Легко проверить, что аксиомы (А1)-(АЗ) и правила (Rl)-(R5) можно интерпретировать в С. Фактически эту интерпретацию можно бы было понимать как обусловленность существования некоторой стрелки в С в случае существования другой.

(например, (R1) означает, что если х®у —> z есть стрелка в С, то стрелка х -" z-=> у принадлежит к С).

Определение 2. Пусть С и С' будут двумя S-категориями (с бифункторами ® и ®' соответственно). S-функтор F: С —" С есть функтор сохраняющий бифункторы, т. е. F (a®b) = F{a)®' F (b).

С помощью соответствующей модификации метода дедекиндовых сечений можно как и в случае N-категорий доказать два следующих предложения [Vasyukov 1995, р.325−326].

Предложение 1. Каждая S-категория имеет полное расширение.

Предложение 2. Пусть U, В, D будут S-категории, где В есть расширение U и D полна. Любой S-функтор F: U —> D может быть расширен до S-функтора Н: В -> D.

Обозначим категорию всех S-категорий, все стрелки которой являются S-функторами, как CatRES, и пусть переменная Л пробегает по множествам стрелок некоторой S-категории. Мы будем иметь дело с отношением ЛиХ|®х₂® … ®х" —" х, что читается следующим образом: стрелка xi®x₂® … ®х" —> х выводима из стрелки тождества и стрелок в Л с помощью категорного перевода (R1) — (R5).

Про стрелку а®а₂® … ®я" -> b говорят, что она Л-значима, если она сохраняется каждым S-функтором подкатегории К с CatRES; говорят, что она будет /^-следствием R, если она сохраняется каждым S-функтором из К всякий раз, когда R сохраняется каждым S-функтором из К.

Теорема 2. ЛиХ|®х₂® … ®х" -> х тогда и только тогда, когда Х]®х₂® … ®х_п —> х является CatRES-следствием Л.

Доказательство. Слева направо доказательство проводим индукцией по выводимости, согласно категорному переводу (А1) и (R1)-(R5). В обратную сторону воспользуемся категорным переводом соответствующих формул из [Buszkowski 1986, р.15], доказанных в LSC:

Ввиду (8) отношение.

(9) a =r b тогда и только тогда, когда Rfr а-> 6и Rb ~^>а для а, ЬеС,

очевидным образом будет конгруэнцией на С, что дает нам фактормножество C/R. Если мы определим для C/R, что ||а|| —> ||6|| будет стрелкой тогда и только тогда, когда ЛИ- а -" Ь, то C/R превращается в категорию предпорядка. А если мы определим ®_к: C/Rx C/R —> C/R как ||а|| ®* ||6|| = ||а®_Л6||, то ®_к становится ковариантным функтором и C/R будет S-категорией. Принимая в расчет, что C//?eCatRES, выводим, что стрелка ||<31||®л|| 11*11 из C/R будет CatRES-следствием R тогда и только тогда, когда Л1Ь а®а_г® … ®а" -> Ь. я

Следствие. II- а®а2® … ®а_п —> Ь тогда и только тогда, когда а®а₂® … ®а" -> b будетCatRES-значимой.