Последовательные алгоритмы решения задачи о доминировании

Пусть Справедлива следующая теорема.

Теорема 39. Пусть ЗИП I = (XdomiV, Pdom) — п-мерная задача о доминировании, т. е. задача типа Sdom, где V = к. Пусть Т — базовое множество, определяемое соотношениями (3.15)—(3.18), п ^ ^ 1. Пусть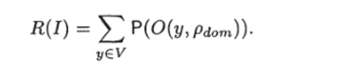

Тогда, если функция плотности вероятности р (х) ^ с, то

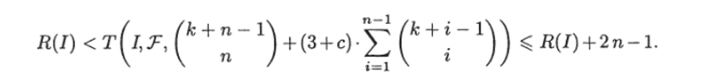
Приведем алгоритм, обеспечивающий мгновенное решение задачи о доминировании, и тем самым докажем теорему 39, поскольку нижняя оценка следует из теоремы 4.

Мы рассмотрим отдельно две возможности: одномерную задачу о доминировании и многомерную.

Одномерный случай.

В данном пункте мы рассмотрим одномерную задачу о доминировании, т. е. случай, когда п = 1.

Пусть V = (у¹,…, у*}, где у* 6 [0,1], г = 1, к. Будем считать, что записи в V упорядочены в порядке возрастания, т. е.

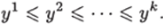
Остается заметить, что отношение pdom при п = 1 есть отношение линейного предпорядка. Поэтому, как показано в доказательстве теоремы 35, ИГ U, изображенный на рис. 3.20, разрешает ЗИП /, и его сложность равна.

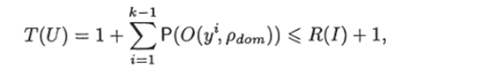
а объем равен Q (U) = п.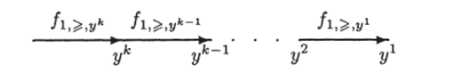

Рис. 3.20. Граф для одномерной задачи о доминировании

Многомерный случай.

В данном пункте мы рассмотрим многомерную задачу о доминировании, т. е. случай, когда п > 1.

Введем вспомогательные обозначения.

Если V С Ydom, г € [0,1] и 1 ^ *1 < • • • < ii ^ п, то обозначим.

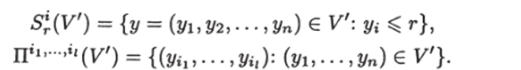
Пусть у¹ = (уу²,…, у% где i = 0, п — 1. Здесь и далее под значком у⁰ будем понимать пустое место или отсутствие значка; так, например, запись М¹(у°) будем понимать как М

Пусть М — некоторое конечное, упорядоченное по возрастанию множество точек из отрезка [ 0,1]. Пусть у? М. Пусть у" — следующая за у точка в М, если у — нс последняя вМ, иу" = 1, если у — последняя точка в М. Обозначим.

Введем по индукции следующие обозначения. Базис индукции. Обозначим.

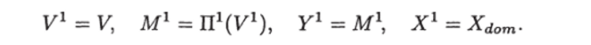
Шаг индукции. Пусть i € {2,п} и для всех j € {1,1 — 1} определены множества.

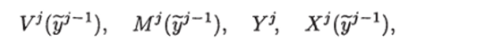
где y^{j 1} = (yy²,—., yⁱ ') — !

произвольный вектор из У⁷«¹. Пусть у^г~¹ = (г/¹, j/²,. -, 3/*»¹) — произвольный вектор из У*" ¹. Тогда обозначим.

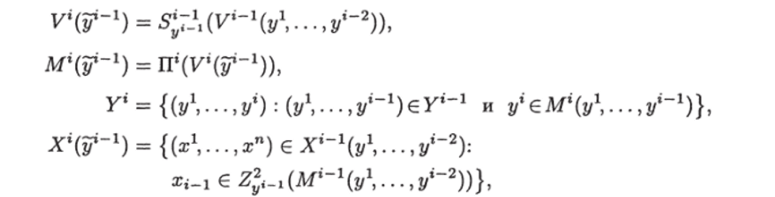
где Zy (M) определяется соотношением (3.19).

Построим по индукции некоторый информационный граф U_q (q 6 {l, n — 1}), который удовлетворяет следующим условиям:

• 1. Граф U_q имеет (У*⁷) листьев.
• 2. Между Y^q и множеством листьев графа U_q можно установить взаимно однозначное соответствие, такое, что если листу а граБазис индукции, q = 1.

Возьмем множество М¹ и упорядочим его по возрастанию. Построим для него граф решающий вторую задачу о близости так, как было описано в разделе 2.3, где в качестве параметра т возьмем т =.

= ]с-|МЧ[.

Заменим в графе U^ переключатель g^ на, а все переключатели вида д^_У0 на gi,>,_y0i где переключатели p_lt.,_m и дг,>,_У0 описываются соотношениями (3.15) и (3.16) соответственно. Полученный граф обозначим U. Покажем, что граф U удовлетворяет условиям утверждения индукции.

Так как У¹ = М то граф U имеет |У¹1 листьев и, следовательно, удовлетворяет условию 1 утверждения индукции.

Легко видеть, что в результате смены нагрузки переключательных вершин граф U на множестве запросов X¹ решает следующую задачу о близости: он позволяет для произвольного запроса х = (xi,…, x_n) G 6 X¹ находить такую точку из М которая является ближайшей слева к числу xi, т. е. к первой координате вектора х. Откуда сразу следует, согласно теореме 1, что если у — произвольная точка из М¹ (а, значит, и из У¹) и, а — лист, которому соответствует точка у, то.

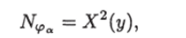
что и доказывает выполнение условия 2 утверждения индукции. Подсчитаем сложность графа U. Обозначим.

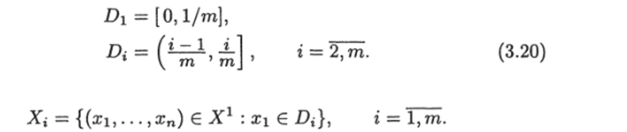
Пусть Тогда так же, как в доказательстве теоремы 19, можно получить, что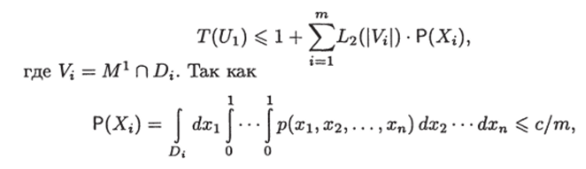

Что и доказывает выполнение условия 3 утверждения индукции.

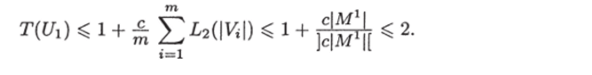
Объем графа U был подсчитан в доказательстве теоремы 19, и он равен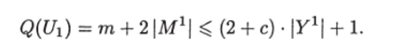

Следовательно, выполняется условие 4 утверждения индукции.

Индуктивный переход. Пусть 1 < q < п и построен граф U_q~ i, удовлетворяющий условиям индукции. Покажем, как можно построить граф U_q.

Возьмем произвольный лист, а графа U_q-. Пусть ему соответствует вектор (у¹,…, у^ч~¹) из Y^q~ Упорядочим по возрастанию множество М^ч(у…, У⁴'¹) — Построим для него граф решающий вторую задачу о близости, так, как было описано в разделе 2.3, где в качестве параметра т возьмем т = ]с • |М^я(у…, г/*⁷⁻¹)| [•.

Заменим в графе U^ переключатель g^ на, а все переключатели вида на д_ъ>,_У0, где переключатели д_ч,.,_т и д_ч,>,_{У (3} описываются соотношениями (3.15) и (3.16) соответственно. Полученный ИГ обозначим U_a.

Уберем нагрузку листа а и объявим его обычной вершиной, после чего отождествим его с корнем графа U_Ql т. е. U_a будет расти из а.

Проделаем такую операцию для каждого листа графа U_q- и полученный в результате граф обозначим U_q. Покажем, что граф U_q удовлетворяет условиям утверждения индукции.

Поскольку множество Y⁴ строится таким образом, что каждый вектор (у¹,…, у⁹⁻¹) из У⁹⁻¹ порождает |М^ч(у …, г/⁹«¹)] векторов множества У⁹, и поскольку из каждого листа графа U_q-1, которому соответствует вектор (у¹,…, у⁹⁻¹) из У⁹⁻¹, выпускается граф, имеющий |М⁹(у¹,. • • > 2/⁹» «¹)! листьев, то граф U_q имеет ровно |У⁹| листьев; тем самым доказано выполнение условия 1 утверждения индукции.

Покажем, что выполняется условие 2 утверждения индукции. Для этого рассмотрим произвольный лист, а графа U_q-. Пусть ему соответствовал вектор (у¹, • •., у⁹⁻¹) из У⁹⁻¹. Согласно предположению индукции функция фильтра листа а такова, что пропускает в лист а только запросы из множества X^я (у …, у⁹⁻¹). Легко видеть, что в результате смены нагрузки переключательных вершин граф U_a решает следующую задачу о близости: он позволяет для произвольного запроса а; = (a?i,…, х_п) 6 Х^я(у…, у⁹⁻¹) (поскольку только эти запросы достигают листа а) находить такую точку из М^я(у…, у⁹⁻¹), которая является ближайшей слева к числу x_q, т. е. к q-й координате вектора х. Откуда сразу следует, согласно теореме 1, что если у — произвольная точка из М^я(у, у⁹⁻¹) (и, значит, (у¹,…, у⁹⁻¹, у) принадлежит Y⁴)

и о/ — лист, которому соответствует точка у, то.

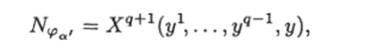
и листу а' можно сопоставить вектор (у¹,…, у^я~^{1_уу) из У*7, что и доказывает выполнение условия 2 утверждения индукции.}

Подсчитаем сложность графа U_q.

Возьмем произвольный лист а графа U_q-. Пусть ему соответствовал вектор (у¹,…, у⁹«¹) из У⁹» ¹. Согласно предположению индукции, только запросы из множества X^я(у¹,… _Уу^я~¹) достигают листа ос. Переобозначим это множество в Х^а. Переобозначим множество М^я(у… _Уу^я~¹) в М^а, а множества Z^_i(M^t(y¹_i. •, у*"¹)) -bZ", где.

i = l_yq — 1. Тогда легко видеть, что.

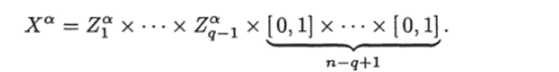
Подсчитаем сложность графа U_a. Обозначим.

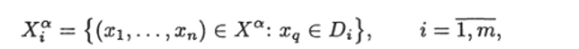
где т = ]с|М^а|[, D{ определяются соотношениями (3.20). Тогда так же, как в доказательстве теоремы 19, с учетом того, что в а попадают только запросы из Х^а, можно получить, что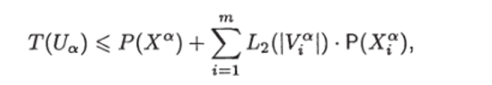

где V* = М^а П Di. Так как.

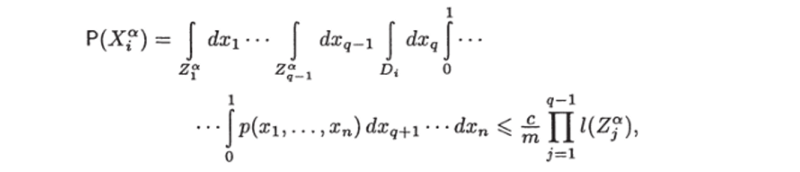
где через l (Z") обозначена длина отрезка Z®, то согласно лемме 14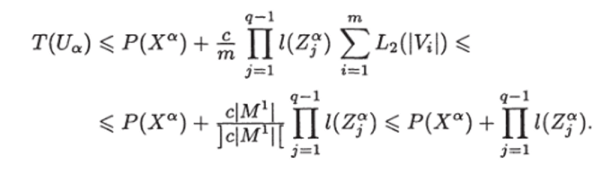

Откуда следует, что и Теперь заметим, что если а, а⁷ € C (U_q-) (т. е. а и а⁷ — листья графа U_q-i) и, а ф а⁷, то Х^а П Х^а = 0. Кроме того,.

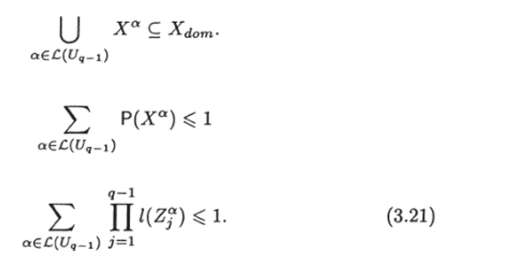
Неравенство (3.21) следует из того, что величина П>=} Равна объему многомерного параллелепипеда Х^а, а сумма объемов всех параллелепипедов Х^а не превышает объема параллелепипеда Xj_om, то есть 1.

Следовательно,.

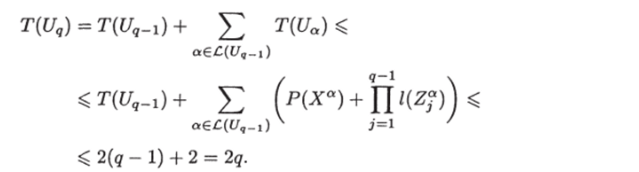
Таким образом, условие 3 утверждения индукции выполняется. Подсчитаем объем графа U_Q.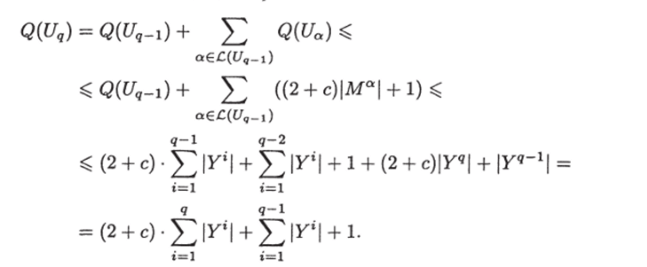

Следовательно, условие 4 утверждения индукции выполняется. И, значит, нам удалось построить граф U_q) который удовлетворяет всем условиям утверждения индукции.

Строить граф С/, обеспечивающий мгновенное решение многомерной задачи о доминировании /, будем следующим образом. Возьмем граф U_n- и рассмотрим произвольный лист а этого графа. Пусть ему соответствует вектор (у¹, …, y^n₁) из У" «¹. Возьмем множество V^й(у¹,…, у^п-1) и переобозначим его в V^е*. Пусть у, — = (у/,…, у») (t = = 1,?), V^a = {yi,…, у*}, где записи упорядочены по возрастанию последней координаты. Построим граф изображенный на рис. 3.21. Уберем нагрузку листа а и объявим его обычной вершиной, после чего отождествим его с корнем графа U'_a, т. е. U‘_а будет расти из а.

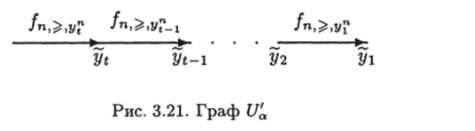
Проделаем такую операцию для каждого листа графа ?/_n-i и полученный в результате граф обозначим U.

Покажем, что граф U разрешает задачу /.

Пусть ос — произвольный лист графа U_n- и пусть ему соответствовал вектор (у¹,. •, у^п-1) из У^п. Переобозначим множество.

Х^п(у—-, У^п~¹) в Х^а.

Возьмем произвольный запрос х = (xi,…, x_n) е Xd_om. Рассмотрим два случая.

Первый случай: существует такой лист а графа {/_п-ь что х G X^е*. Это означает, что запрос х достигнет листа, а и ни в какие другие листы графа ?/_n-i не попадет, так как для любых различных а', а" € C (U_n-1) справедливо Х^а П Х^а = 0. Из листа, а исходит цепочка, вершинам которой сопоставлены записи из множества Vⁿ(y…, y^n₁), а это множество есть не что иное, как множество всех записей из V, у которых г-я координата не превышает у* (г = 1, п — 1). То, что х G Х^а, означает, что у¹ — ближайшая слева точка к х в М у² — ближайшая слева точка к хг в М²(у¹), которое представляет собой проекцию на вторую координату множества V²(y¹), и т. д. Таким образом, множество Vⁿ(y¹,…, y^n₁) содержит все те и только те точки из V, которые удовлетворяют первым гг — 1 неравенствам (3.14). Далее запрос х продвигается вдоль цепочки, растущей из а, пока записи из Vⁿ(y¹,…, y^n₁) не больше по последней координате, чем х". Тем самым ответ на запрос х будет содержать только те записи, которые удовлетворяют запросу, причем все такие записи.

Второй случай: для любого a G C (U_n-) запрос х ^ Х^а. Это означает, что запрос не дойдет ни до одного из листьев графа (/_п-ь и, значит, ответ на запрос х будет пуст. Осталось показать, что при таком х в библиотеке V не содержится записей, удовлетворяющих х.

Пусть i G {1,п — 1} — такой номер, что существует такой набор (у¹,…, у*^-1) из У*"¹, что х € X^х(у…, у*"" ¹), и для любого набора (у¹" • - - > У*) из У* запрос х? -ЛГ*⁺¹(у¹,…, у*). Очевидно, что такой номер есть, так как х 6 X¹ = Xdom• Так как для некоторого набора (у¹,…, у*"¹) из У*^-1 выполняется х € -ХДу¹,…, у*^-1) (очевидно, что такой набор только один), то запрос х пройдет в лист 7 графа Ui-u которому соответствует набор (у¹,…*у*"¹) (если i = 1, то в качестве 7 рассматривается корень графа U). Из листа 7 растет граф, который решает вторую задачу о близости для множества М^г(у…, у*^-1), и так как для любого набора (у¹,…, у*) из У* запрос х & Х^г+1(у…, у*), то это, значит, что х, меньше чем любая точка из М'(у …, у*^-1), т. е. в множестве V*(y…, у*"¹), которое состоит из записей, удовлетворяющих первым i — 1 неравенствам из (3.14), не найдется ни одной точки, t-я координата которой не больше чем х,. Следовательно, в V нет записей, удовлетворяющих запросу х.

Тем самым мы показали, что граф U разрешает задачу I.

Подсчитаем сложность графа U.

Рассмотрим произвольный лист а графа U_n~. Пусть ему соответствовал вектор (у¹,…, y^n₁) из У^п₁. Цепочку ребер, растущую из а, обозначим через U'_a. Переобозначим множество У^Л(у¹,…, у^п₁) в V^a_y ^а Х^п(уу" ^-1) в Х^а.

Легко видеть, что сложность графа U'_а равна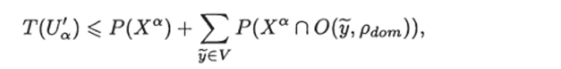

откуда.

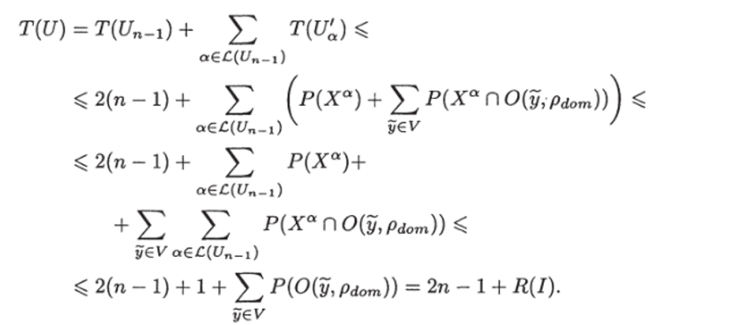
Подсчитаем объем графа U. Для этого оценим величины Y^q, где q = 1, п. Понятно, что если библиотека V такова, что ее проекция на любую ось координат имеет мощность А, то величины Y^q будут достигать максимума, и в этом случае эти величины будут зависеть только от к и q. Покажем индукцией по у, что для такого рода библиотек Y^q =

Базис индукции, q = 1. Тогда.

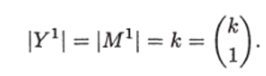
Индуктивный переход. Пусть для любого i € {1,д — 1} справедливо |У*| = Напомним, что по построению количество листьев в графе U_q равно |У*|. Рассмотрим граф U. Пусть У¹ = М¹ = = {yi,…, у*}, где yi < Уг < • * • < У к- Обозначим через о;* лист графа U, которому соответствует точка у,, а через U? — подграф графа U_q, растущий из листа а*. Легко заметить, что U? и U_q- изоморфны как графы при А; = г и, значит, число листьев графа Uпо предположению индукции равно Откуда число листьев графа U_q равно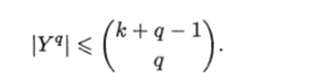

Последнее равенство можно найти в качестве упражнения, например, в (13, стр. 262].

Тем самым мы показали, что для любой библиотеки V и любого q Е {1, гг} величина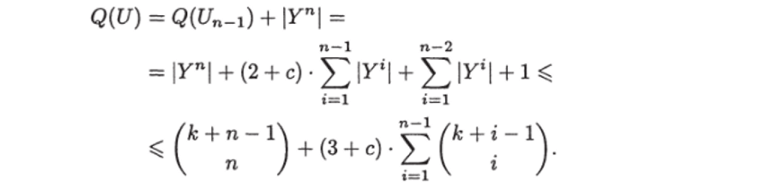

По построению графа U легко видеть, что объем графа U равен объему графа U_n~ плюс количество листьев в графе U, так как помимо ребер графа U_n- в графе U есть только ребра, ведущие в листья, и на каждый лист приходится ровно одно ребро. По аналогии с тем, как мы определяли число листьев в графе U_q, легко показать, что число листьев графа U равно |У^П|. Следовательно,.

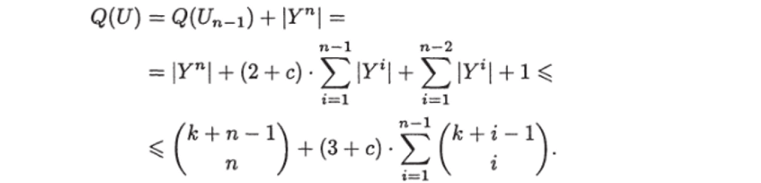
Тем самым, теорема 39 полностью доказана.