Основы линейной теории тонких оболочек

Сведения из дифференциальной геометрии поверхностей

Ниже приводятся формулы из дифференциальной геометрии пространственных кривых и поверхностей, которые необходимо знать для понимания этого и последующих подразделов гл. 7 учебника.

Способы задания кривой. Существует семь основных способов задания кривых.

1. Параметрические уравнения пространственной кривой.

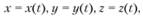
где t — переменный параметр.

2. Векторное уравнение пространственной кривой.

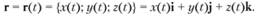
3. Любая кривая определяется своими кривизной k (s) и кручением k (s) однозначно с точностью до ее движения в пространстве:

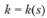и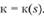

4. Задание плоской кривой в полярных координатах.

Полярная система координат на плоскости задается точкой О (полюс) и направленной прямой Ох (полярная ось);? — полярный угол; r(?) — полярный радиус.

• 5. Линия пересечения двух поверхносте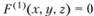й и 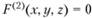представляет собой кривую, точки которой удовлетворяют каждому из двух уравнений.
• 6. Реже пространственные, чаще плоские кривые могут быть заданы в явной форме:

z = z (х, у) — явное уравнение пространственной кривой; у = у (х) — явное уравнение плоской кривой.

7. Кривую можно задать и в неявной форме;

F (x, y, z) = 0 — неявное уравнение пространственной кривой;

F (x, у) = 0 — неявное уравнение плоской кривой.

Касательная и главная нормаль. Касательную в данной точке кривой M (t) можно рассматривать как прямую, проходящую через эту точку 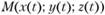по направлению вектора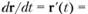 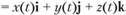, поэтому радиус-вектор точки на касательной прямой имеет вид.

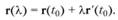
Уравнение касательной прямой к пространственной кривой можно записать также в форме.

где ?, ?,? - текущие координаты.

Главная нормаль кривой задается вектором.

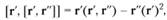
где штрихами показаны производные по параметру t, квадратными скобками обозначено векторное произведение векторов.

Длина дуги кривой. Выражение для вычисления длины дуги кривой можно представить в виде.

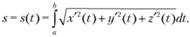
Способы задания гладких поверхностей. Поверхность может быть задана тремя параметрическими уравнениями.

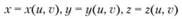
в неявной —  — или явной — 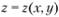 — форме. Во многих случаях поверхность удобно задавать векторным уравнением.

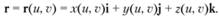
Если положить и = const или V = const, то уравнения поверхности будут представлять собой уравнения кривых двух семейств. Линия и = const называется v-линией, а линия v = const — u-линией. Линии и, v называются криволинейными координатными линиями на поверхности.

Касательная плоскость к поверхности. Пусть поверхность задана неявным уравнением вида F (x, у, z) = 0. В этом случае уравнение касательной плоскости к поверхности будет иметь вид.

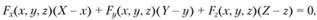
где X, Y. Z — текущие координаты.

Обозначая через X, Y, Z текущие координаты для касательной плоскости к поверхности 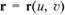, можно записать уравнение этой плоскости в виде.

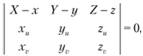
где нижние индексы означают частное дифференцирование по соответствующему параметру.

Нормаль к поверхности. Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания. Уравнение нормали легко составить как уравнение прямой, проходящей через данную точку М (х, у, z) в заданном направлении:

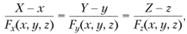
где X, Y, Z — текущие координаты.

Пусть поверхность задана своим радиус-вектором ,.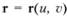

тогда векторное произведение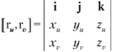

указывает направление нормали к поверхности в данной точке, а единичный вектор нормали? к поверхности определяется по формуле.

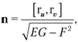
где E, F, G — коэффициенты первой квадратичной формы поверхности.

Формулы для вычисления коэффициентов основных квадратичных форм поверхности. Дифференциал длины дуги ds гладкой кривой на гладкой поверхности 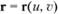выражается формулой.

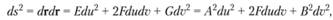
где А, В — коэффициенты Ламе в теории поверхностей.

Коэффициенты первой квадратичной формы поверхности 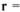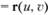в развернутом виде принимают вид.

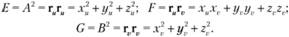
Коэффициенты второй квадратичной формы поверхности 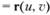в развернутом виде принимают вид.

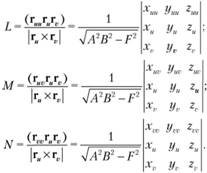
Во всех формулах одиночные нижние буквенные индексы означают первую частную производную по соответствующему параметру, нижние двойные одинаковые буквенные индексы — вторую частную производную по соответствующему параметру, нижние двойные разные буквенные индексы — вторую частную смешанную производную. Три вектора, заключенные в круглые скобки, означают смешанное произведение векторов.

Длины кривых и углы между кривыми на поверхности. Если ищется угол? между криволинейными координатными линиями и, ?, то используется формула.

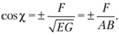
Если координатные линии и, v пересекаются под прямым углом, то F= 0. Если М = 0, то говорят, что координатные линии и, v — сопряженные.

Длина криволинейной координатной линии и, принадлежащей поверхности :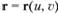

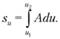
Длина криволинейной координатной линии v, принадлежащей поверхности :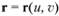

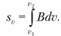
Площадь фрагмента поверхности. Для вычисления площади всей поверхности или ее фрагмента применяется формула.

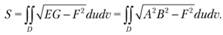
Кривизны линий на поверхности и кривизны поверхности. Существует два взаимно ортогональных направления на поверхности, называемых главными направлениями, в которых кривизны 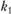имеют экстремальные значения 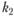и 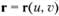. Эти кривизны называют главными кривизнами. Если F= М = 0, то криволинейные координатные линии и, v совпадают с главными направлениями и будут называться линиями главных кривизн.

Кривизны криволинейных координатных линий и, v на поверхности :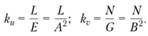

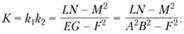
Гауссова (полная) кривизна поверхности:

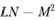
Знак гауссовой кривизны определяется выражением 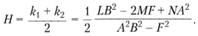Гауссова кривизна положительна в эллиптических точках, отрицательна в гиперболических точках и равна нулю в параболических точках и точках уплощения.

Средняя кривизна поверхности:

Главные кривизны 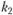, 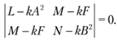поверхности есть корни квадратичного уравнения.