Методы Монте-Карло, использующие марковские цепи

Методы выборки по значимости и выборки с отклонением значений успешно работают, только если аппроксимирующее распределение Q (x) близко к исследуемому Р (х). При этом данные методы генерируют элементы выборки, независимые друг от друга, фактически производя «случайное» исследование функции распределения Р (х). Несколько иной подход применяется в методах Монте-Карло, основанных на марковских цепях. Эта группа подходов производит постепенное исследование функции распределения, где каждое последующее значение определенным способом зависит от предыдущего, фактически представляя марковскую цепь. Данный подход позволяет исследовать сложные функции распределения, для которых неизвестны (или отсутствуют) удовлетворительные аппроксимирующие распределения.

Алгоритм Метрополиса — Гастингса. Этот простой алгоритм семплирования несколько похож на алгоритм формирования выборки с отклонением значений, так как отбор новой точки происходит через состояние-кандидат. Отличие состоит в том, что если в алгоритме выборки с отклонением значений используется статичная аппроксимирующая функция распределения, то в алгоритме Метрополиса — Гастингса данная функция меняется с каждым шагом и отсутствует требование (2.66) (рис. 2.28).

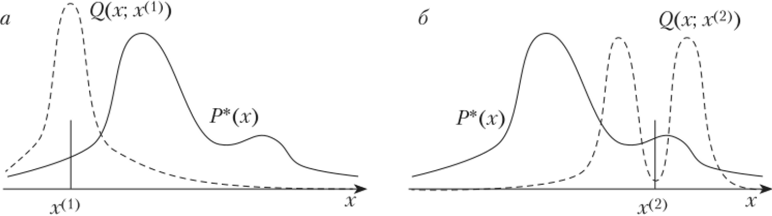
Рис. 2.28. Два примера (ап б) различных аппроксимирующих функций, используемых в алгоритме Метрополиса — Гастингса.

На рис. 2.28 приведены два варианта аппроксимирующей функции распределения (пунктирная линия). В ходе каждой итерации функция Q (x, х') центруется в месте расположения текущего значения х', и на основании данной функции случайным образом (с учетом закона распределения Q) определяется следующее значение-кандидат. Принятие значения производится по следующему правилу:

1) сначала рассчитывается отношение.

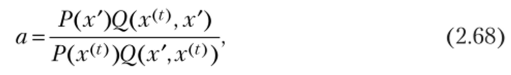
где х' — новое значение-кандидат; х<0 — текущее значение выборки (в итерации t). Фактически данное отношение показывает баланс вероятностей между нахождением в состоянии х' и переходом из состояния х! в состояние х (⁽ и наоборот;

2) если это отношение больше или равно единице, то новое состояние принимается с вероятностью 1. Если отношение меньше единицы, то оно принимается с вероятностью а;

3) если состояние принимается, то состояние в итерации л^⁺¹) = х', иначе состояние х0⁺¹> = №?

Алгоритм Гиббса. Алгоритм Гиббса используется для получения совместной выборки нескольких взаимосвязанных случайных величин. Как и в случае других методов формирования выборки, применять этот метод следует, когда само распределение п случайных величин Р (х_{} х₂, …, х_п) слишком сложно для прямого семнлирования. При этом для работы данного алгоритма требуется, чтобы была возможность напрямую работать с условными распределениями Р (х_х х₂,…, х_п), Р (х₂ x_t,…, х_п) … Р (х_п x_lf х₂, …, х_п__х). Сам алгоритм достаточно прост — в ходе каждой итерации (t + 1) производится последовательное получение новых значений x^^t+i…, на основании значений переменных предыдущей итерации и упомянутых выше условных вероятностей: