Детерминированное свидетельство. 
Локальный апостериорный вывод в алгебраических байесовских сетях как система матрично-векторных операций

Выделяют две задачи апостериорного вывода.

Решением первой задачи апостериорного вывода во фрагменте знаний является оценка вероятности появления свидетельства при заданных оценках.

Решением второй задачи апостериорного вывода во фрагменте знаний является оценка условных вероятностей всех конъюнктов АБС относительно поступившего свидетельства.

Детерминированным свидетельством в теории АБС называют такое свидетельство, которое сообщает нам о том, что некоторый набор атомов положительно означен, а некоторый — отрицательно. Детерминированные свидетельства удобно представить в виде конъюнкта положительно означенных атомов и конъюнкта отрицательно означенных. Ниже приведен пример двух свидетельств:

.

.

Конъюнктам положительно и отрицательно означенных атомов удобно сопоставить индексы, которые однозначно определят свидетельство над заданным набором атомов.

Опишем решение первой задачи апостериорного вывода для детерминированного свидетельства над фрагментом знаний. Свидетельство можно представить как пропозициональную формулу. Обозначим формулу, соответствующую свидетельству через, например:. Вычисление вероятности произвольной пропозициональной формулы — это задача априорного вывода. С априорным выводом в общем случае можно ознакомиться, например, в [3]. Здесь же мы решим ее для конкретного вида формул. Пусть задан ФЗ с точечными оценками истинности, тогда вероятность может быть легко вычислена как. Здесь играет роль важная особенность квантов, состоящая в том, что конъюнкция кванта с любой пропозициональной формулой — это либо сам квант, если он входит в СДНФ данной формулы, либо ложь. То есть нам остается лишь определить, какие кванты входят в СДНФ, а какие — нет. Пользуясь побитовыми логическими операциями можно записать как:

В этой формуле и далее по тексту обозначает побитовое «и», а — побитовое отрицание.

Перейдем теперь ко второй задаче апостериорного вывода. Вначале рассмотрим фрагмент знаний с точечными оценками истинности, то есть нам задан вектор. На его основе, по формуле (1) можно построить вектор. Заметим, что полученный вектор содержит в себе информацию о вероятностях всех квантов над нашим алфавитом. Будем строить вектор условных вероятностей относительно нашего свидетельства. Согласно определению условной вероятности.

.(4).

Вероятности и мы уже научились вычислять выше. Запишем (4) в виде векторов:

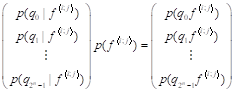
.(5).

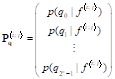
Введем обозначение. Запишем, что. Тогда (5) принимает вид.

.(6).

Теперь нам необходимо описать структуру матрицы. Основываясь на (3) получаем.

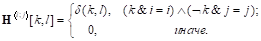
(7).

Матрица имеет очень четкую структуру и может быть записана с использованием тензорного (кронекерова) произведения следующим образом:

.(8).

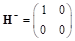
Если ввести обозначения, , то матрица может быть вычислена следующим образом:

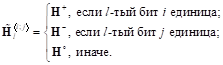
(9).

В формуле (6) используются условные (слева) и маргинальные (справа) вероятности квантов. Но мы знаем, что вероятности на квантах выражаются через вероятности на конъюнктах по формуле (1). Обозначим верктор условных вероятностей на конъюнктах через и проведем замену по формуле (1), чтобы получить:

.

Домножив обе части слева на, получаем:

(10).

Вспомним, что все приведенные в вышестоящей формуле матрицы могут быть представлены в виде произведений Кронекера, которое в свою очередь обладает следующим свойством [1]:

.

Воспользовавшись этим свойством, получаем:

.

Рассмотрим матрицы и построенную на их основе. По аналогии с можно выразить :

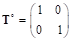
И соответственно:, , .

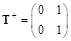
Применив новое обозначение к (10), получаем:

(11).

Заметим, что если вычислить, то нет необходимости отдельно вычислять. Это связанно с тем, что по определению — нулевой элемент вектора — равен единице, а, следовательно, нулевой элемент равен в точности. Предполагая, что, получаем:

(11').

Полученная формула дает нам точное выражение для апос-териорной вероятности элементов ФЗ при поступившем свидетельстве, если исходные оценки были скалярные (т.е. оценки вероятности конъюнктов имели вид, где — числа из интервала), а свидетельства — детерминированные. Если оценки были не скалярные, а интервальные, то нам потребуется решать серию ЗЛП [5].

Пусть задан ФЗ с оценками и, тогда опишем ЗЛП для получения апостериорной вероятности на элементах ФЗ. Если записать все в явном виде, то получаемые задачи не будут задачами линейного программирования, а будут относиться к классу так называемых задач дробно-линейного программирования. В [2] показано как в общем случае задачи дробно-линейного программирования можно свести к задачам линейного программирования. Здесь мы построим конкретный (частный) случай подобного сведения.

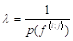
Рассмотрим новую переменную. Очевидно, что. Произведем замену переменных — введем вектор, тогда (11') принимает вид.

.(12).

Формула (12) — линейная, следовательно можно построить серию задач линейного программирования. Нам потребуется найти максимум и минимум для каждого элемента вектора, кроме нулевого. Нулевой же элемент даст нам дополнительное ограничение вида.

.

Кроме того, будут ограничения, следующие из аксиоматики вероятностной логики [5]:

.

и ограничения, следующие из предметной области [5]:

и .

Решив предложенную серию ЗЛП, мы получим решение второй задачи линейного программирования.