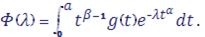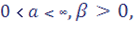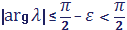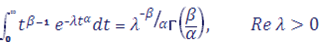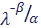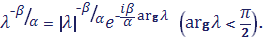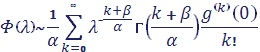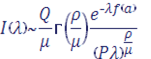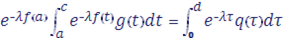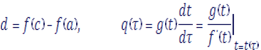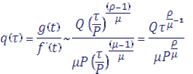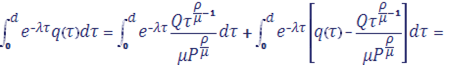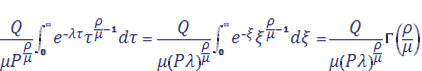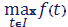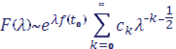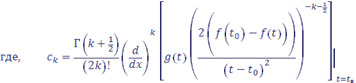Обоснование метода Лапласа. 
Основные утверждения Лемма Ватсона

Рассмотрим интеграл Лапласа, в котором — степенная функция:

где. Так как в окрестности точки максимума функцию можно приближенно заменить степенной функцией, то вычисление асимптотики интегралов Лапласа сводится к вычислению эталонных интегралов.

Получим асимптотические оценки для при, где сектор в комплексной плоскости .

>0 может быть выбрано сколь угодно малым, не зависящим от .

Нам понадобится формула:

где. Для функции выбрана главная ветвь:

Если >0, то с помощью замены переменной интеграл приводится к Г-функции Лемма (Ватсона): Пусть, Тогда при >?,, справедливо асимптотическое разложение:

разложение можно дифференцировать по любое число раз.

— класс непрерывно дифференциремых на функций.

Если функция непрерывна при и, то при, справедлива асимптотическая формула.

Основная теорема.

Будем считать, что значение «» конечно; полагаем, что максимум функции достигается в точке; в других случаях область интегрирования можно разбить на части точками минимума и максимума функции и, если это необходимо, изменить знак. Пусть «» конечно или бесконечно действительная, а может быть функцией. Кроме того, пусть выполнены следующие условия:

• 1. при и для каждого то есть достигает минимума лишь в точке
• 2. непрерывны в окрестности точки, исключая саму точку.
• 3. При будет и первое из этих соотношений допускает дифференцирование. Здесь положительные постоянные, а — действительная или комплексная постоянная.
• 4. Интеграл:

абсолютно сходится во всей области интегрирования при достаточно больших .

Если выполнены условия 1−4, то:

Доказательство.

1. Из условий 2 и 3 следует, что найдется такое число достаточно близкое к что в интервале функция непрерывна и положительна, а непрерывна. Так как возрастает в то можно в качестве новой переменной интегрирования на этом интервале взять величину:

Тогда — непрерывные функции и:

где:

Очевидно, что значение конечно и положительно, а непрерывна при.

Далее согласно свойству 3 при мы имеем:

следовательно,.

Отсюда:

Используя соотношение перепишем интеграл в виде:

Первый член справа уже даёт искомую асимптотику. В самом деле, осуществляя в этом интеграле замену:

.

получим:

Отсюда и получим результат.

Теорема 1.

Пусть:

— конечный отрезок и выполнены условия 1., 2. достигается только в точке, , 3. при, близких к, и .

Тогда при справедливо асимптотическое разложение:

Главный член асимптотики имеет вид:

Теорема. Пусть все условия теоремы 1 выполнены, за исключением одного, тогда при ,.

Главный член асимптотики имеет вид.