Распределение Фишера28 (F-распределение, распределение дисперсионного отношения)

Пусть случайные величины т|, т]₂,…, r|_m; 1=₂,…, (т и /7 — натуральные числа) — независимы и каждая имеет стандартное нормальное распределение /V (0,1). Говорят, что случайная величина F_{m я}, определенная как.

имеет F-распределение с параметрами тип. Натуральные числа т и п называют числами степеней свободы (рис. 3.6).^[1]

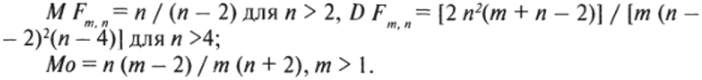
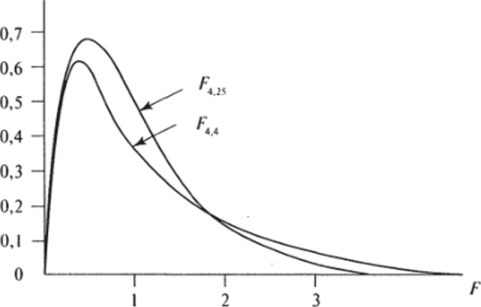
Рис. 3.6. Функции плотности /—распределения с разным числом степеней свободы.

Источник: Гласс Дж. Стэнли Дж. С. 211.

Повторение отдельных фрагментов курса по теории вероятностей

• 1. Общее представление о вероятностных таблицах. Принципы их использования.
• 2. Определение нормальною распределения. Вид нормальной кривой, «физический» смысл отвечающих ей математического ожидания и дисперсии. Целесообразность измерения значения случайной величины в единицах о (среднего квадратического отклонения). Соотношение площадей под нормальной кривой и вероятностей попадания в отрезки (р ± о, р ± 2о, р ± За). Определение размера отрезка (в единицах о) при заданной доле попадания в него. Функция Далласа (П.С. Лаплас (1749—1827) — знаменитый французский математик, астроном).

Следует помнить, каковы доли площадей под разными частями нормальной кривой; учесть, что целому числу, а обычно отвечают «корявые» проценты: одна о — 68,3% площади, 2о — 95,4; а «круглым» процентам отвечает «корявое» число «сигм»: 90% — 1,64о, 95 — 1,96о, 99% — 2, 57о и т. д. Эти и другие значения представлены на рис. 3.7.

Необходимо также понимать связь функции плотности распределения с функцией распределения и принципы нахождения квантилей распределения.

(например, процентилей). Этому также может помочь рис. 3.7, на котором отражено, как из функции плотности получается функция распределения (отвечающая накопленным процентам) и как по функции распределения можно рассчитывать процентили.

Аналогичные иллюстрации можно найти и в других работах, например: Тюрин 10.//., Макаров А.Л. Анализ данных на компьютере. М.: ИНФРА-М, 2003. С. 79; Kachigan S.K. Statistical Analysis. An Interdisciplinar Introduction to Univariate and Multivariate methods. N.Y.: Radius Press, 1986. P. 139.

• 3. Правило трех сигм.
• 4. Роль стандартизации нормально распределенных случайных величин при использовании соответствующих вероятностных таблиц. Применение таблицы для стандартизованной величины при получении характеристик распределения произвольной нормально распределенной случайной величины.

Пример того, как по величине отрезка под стандартизованной нормальной кривой можно определять вероятность попадания в этот отрезок соответствующей случайной величины, показан на рис. 3.7. и 3.8.

• 5. Умение использовать вероятностные таблицы разного вида для нормального распределения. Желательно потренироваться на таблицах разных видов, например:
  • • таблицы значений функции Лапласа Ф (х)**
  • • таблицы, в которой задана вероятность попадания в правый конец графика функции плотности (по заданному z определяется вероятность того, что

fix) >г)^[2];

• • таблицы значений удвоенной функции Лапласа^[3];
• • таблицы верхних процентных точек стандартного нормального распределения^[4].
• 6. Таблицы, составленные для остальных рассмотренных выше распределений. Их разные виды. Квантили распределений. Понимание того, что таблицы, как правило, содержат значения/7-квантилей. Принцип практической невозможности маловероятных событий.

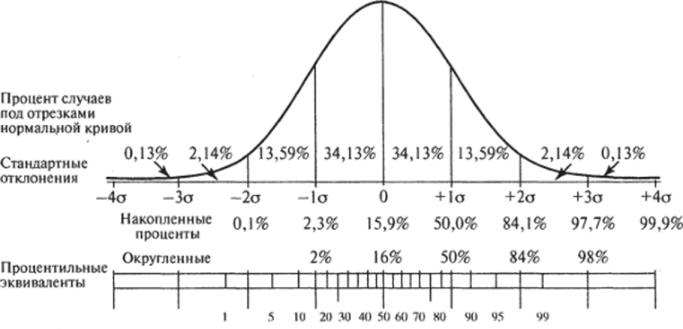
Рис. 3.7. Доли плошадей под разными частями кривой плотности нормального распределения. Указание процентилей

Источник: Гласс Дж., Стэнли Дж. С. 97.

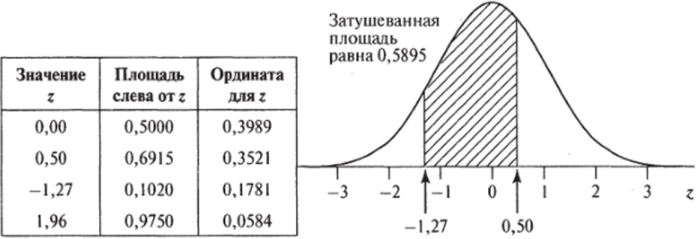
Рис. 3.8. Связь отрезка диапазона изменения стандартизованной нормальной кривой с отвечающей ему площадью.

Источник: Гласс Дж. Стэнли Дж. С. 95.

Примеры задач

• 1. Докажите, что среднее арифметическое значение стандартизованного признака равно нулю, а среднее квадратическое отклонение — единице.
• 2. Известно, что распределение оценок, полученных абитуриентами при ответе на некоторый 20-балльный тест, имеет вид N (10, 3). Какова вероятностьтого, что абитуриент получит балл от 7 до II? Объяснить, как находится подобная вероятность при использовании четырех видов вероятностных таблиц.
• 3. С какой площадью под графиком функции плотности стандартизованного нормального распределения соотносится значение функции Лапласа?
• 4. Как следует понимать выражение «верхние процентные точки» из книги Тюрина и Макарова? В некоторых работах эти точки называются процентилями. Что такое процентиль? Что такое квантиль (частным случаем которого является процентиль)? Какие еще виды квантилей вы знаете?

• [1] Р. А. Фишер (1890—1962) — известный английский статистик. Рассматриваемое распределение он открыл в 1924 г. (см.: Айвазян С. А., Мхитарян В. С. Теория вероятностей и прикладная статистика. С. 145: там же указано, что все рассматриваемыеслучайные величины могут иметь одинаковую дисперсию, отличную от единицы).
• [2] w См., например: Гмурман В. Е. Теория вероятностей и математическая статистика. М.: Высшая школа, 1998. С. 462—463; Колемаев В. А., Калинина В. Н. Теория вероятностей и математическая статистика. М.: ИНФРА-М, 1997; Юнити, 2003.С. 293. *' Эддоус М., Стэнсфилд Р. Методы принятия решения. М.: Финансы и статистика, 1997. С. 575.
• [3] м Калинина В.//., Панкин В. Ф. Математическая статистика. М.: Высшая школа, 1998. С. 331.
• [4] Тюрин Ю. П., Макаров А. А. Анализ данных на компьютере. М.: ИНФРА-М, 2003. С. 496.