Функция Мёбиуса. 
Криптографические методы защиты информации. 
Часть 1. Математические аспекты

Функция Мёбиуса р (гг): N —> {-1, 0, 1}, где ц (/г) = О, если п делится на квадрат простого числа; р (п) = (-1)⁵ в противном случае, где s — порядок базы канонического разложения числа гг; р (1) = 1. Отсюда |т (г?) мультипликативна.

Теорема 5.2. Пусть 9 — мультипликативная функция натуральных чисел, тогда.

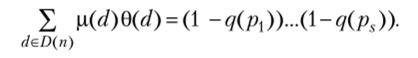
4 По теореме 5.16 функция 6(п) = р (п)В (п) мультипликативна. Тогда по теореме 5.1 г получаем нужное равенство, так как 8(/?) = -9(/?) при простом /?. ?

Следствие 1. При 9(п) = 1 и п > 1 получаем? i (d) = 9. О.

deD (n)

Следствие 2. При 9(?г) = 1/га и п > 1 получаем? V-(d)/d =

deD (n)

= (1−1/_Pl)…(l-1 //?,)•>

Функция Эйлера.

В алгебре, теории чисел и в криптографических приложениях используется функция Эйлера (обозначается ф (я)). Она определена для любого пе N и равна количеству натуральных чисел, не превосходящих п и взаимно простых п, где ф (1) = 1. Мультипликативность функции ф (и) доказана ниже (следствие 1 из теоремы 5.5).

В каноническом разложении (2.1) числа п делитель вида pf называется примарным делителем числа n, j= 1,…, s. Множество примарных делителей числа п состоит из попарно взаимно простых чисел, тогда ф (и) = ц>(р^)…ц>(р^к/) в силу мультипликативности функции (р (п). Из определения функции Эйлера следует: ф (//') = р^к — р^к~¹ при простом р. Тогда.

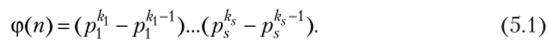
Функция [xj определена для всех действительныхх как наибольшее целое, не превосходящее х. Эта функция называется целой частью отх. Она используется при некоторых вычислениях.

Теорема 5.3. Наибольший показатель t простого/?, при которомр¹ п, равен.

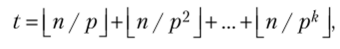
где к = Llog_p«J.

?4 В произведении и! число т, сомножителей, кратных р‘, равно 1_п / р’Х в каждый такой сомножитель число р входит i раз, i = 1, …, к. Сомножитель, кратный p^k+i, в произведение не входит. Каждый сомножитель в п, кратный р но не кратный pⁱ⁺ⁱ, учтен i раз как кратный р, р²,…, р‘, i = 1,…, к. Тогда общее число вхождений р в разложение п равно т_х + т₂ + … + т_к. ?

Теорема 5.4 (малая теорема Ферма). Пусть р — простое число, тогда для любого а е Z

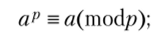
если а не сравнимо с 0 по mod/?, то.

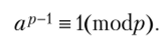
4 Для а кратных р первое сравнение тривиально.

Если р не делит а, то множество чисел {Оа, 1″, 2а, …, (р — 1)"} образует полную систему вычетов. Если это не так, то га = ja (modp) при некоторых i, j е {0, 1, р — 1}, / < j. Тогда р | j — i, что возможно лишь при j = i. Тогда множество чисел {la (modp), 2"(modp),(/? - l) a (modp)} есть перестановка всех ненулевых элементов поля Z_p, следовательно, (р — 1)! = = (р — l)!"P^_1(mod/?). Поскольку р не делит (/? — 1)!, то отсюда р af^}~^{ — 1, т. е. аР~^х = l (mod/?).

Домножив на а обе части последнего сравнения, получим сравнение aJ^> = «(mod/?) для а, не кратных /?. ?

Следствие. Если р не делит а и п = ra (mod (/? — 1)), то а^п = «'» (mod/?).

4 Если п = т, то утверждение верно. Пусть п > т, тогда п = т + с (р — 1) для некоторого се N. Умножив почленно с сравнений «/^м = l (mod/?), получим нужный результат. ?

Пример 5.1.

Найдите последнюю цифру в 7-ичной записи числа 2^[1][2][3] оооооо Решение

Пусть р = 7. Вычисляем: 1 000 000(mod(р — 1)) = 1 000 000(mod6) = 4, тогда по следствию из теоремы 5.4 2^{1 000 000} = 2^[4]= 16 s 2(mod7).

Ответ: 2.

Пусть п нечетно. В силу мультипликативности функции получаем.

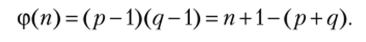
Значит, ф (и) можно вычислить по известным/? и q, выполнив одно сложение и одно вычитание, т. е. за O (logrc) двоичных операций.

Обратно, для величин р и q известны их произведение и сумма: р + q = = п + 1 — ср (л?). Правая часть четная, обозначим ее 2Ь. Тогда р и q — корни квадратного уравнения z² — 2bz + п = 0, т. е. р и q равны b±Jb² — п. Трудоемкость вычисления корней определяется извлечением квадратного корня, требующим порядка 0(log³a) двоичных операций. ?

Следствие 3. Для любого натурального п выполнено:? ф (гУ) = п-

deD (n)

М Обозначив 0(я) левую часть равенства, покажем мультипликативность этой функции, т. е. в (пт) = в (п)в (т) при (п> т) = 1.

Любой делитель d числа пт единственным образом представляется в виде d = 5 т, где 51 я, т | т и (5, т) = 1 в силу (п, т) = 1. Из мультипликативности функции ф следует: ф (5т) = ф (5)ф (т), т. е. имеется биекция D (nm) D (n) х D (m) и.

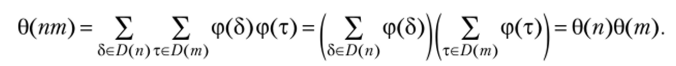
В силу мультипликативности функции 0 с учетом канонического разложения числа п имеем: 0(п) = 0(/?^)…0(/?/). Докажем, что 0(/?*) = р^к. Поскольку D (p^k) = {1, р,…, р^к}, то.

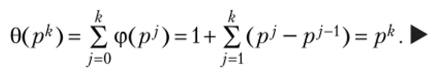
Теорема 5.6 (Эйлер). Если (ш, а) = 1, то a^<p (^w) = l (modm).

Ч Проведем индукцию по Ь. Пусть т = р^ь — степень простого числа. При b = 1 имеем малую теорему Ферма. Пусть b > 2, и формула верна для т = р^ь~^х. Тогда aP^b~^x~P^b~² = 1 +р^ь~^хс для некоторого целого с. Возведем обе части равенства в степень р. Поскольку все коэффициенты в выражении (1 + x)i кроме первого и последнего, делятся на р> то получаем, что _ар^ъ-р^ъ~ 1 превышает на 1 сумму, каждое слагаемое которой делится на р^ь. Отсюда а^^р,)) = l (mod/?⁶). Следовательно, при любом пе N

Если р^ь — примарный делитель числа т, то из мультипликативности функции ф следует, что ф(т) = ф (р^ь)<�р (т /р^ь). Тогда из (5.2) при п = (р (т/р^ь) получаем: = l (modp^/;). Последнее равенство верно для любого примар;

ного делителя числа т. Поскольку примарные делители числа т попарно взаимно просты, то сравнение выполнено и по модулю т. ?

Следствие. Если (т_} а) = 1, г — наименьший неотрицательный вычет гг (шобф (т)), то а^п= a^r(modm).

М При п = г утверждение верно. Пусть п > г, тогда п = г+ сср (т) для некоторого с е N. Умножив почленно с сравнений лч>(^от) = l (modm), получим нужный результат. ?

Теорема Эйлера следует также из равенства а^{0 Т (}*^а = 1 и теоремы Лагранжа, в соответствии с которой для элемента а группы Z_m* верно orda|(p (m).

Применим теоремы для выполнения экономных вычислений.

Пусть требуется вычислить bⁿ(modm) для натуральных Ь, п, тп. Предложим алгоритм, выполняющий после каждого умножения приведение чисел по mod/rz (при этом без ущерба для общности можно считать, что b < ш), тогда вычисления выполняются только над числами, меньшими т².

Пусть (п₀, п_{, …, Щ__х) — двоичное представление числа п. Последовательно возводя в квадрат число b и приводя результаты по modm, вычисляем fe²(modm), b⁴(modm), …, b^2k~modm). Попутно вычисляем произведения а₀, а и a_k__v где а₀ = bⁿ< а_х = a₀b²ⁿi = bⁿ^²ⁿ i, a_k__x = а_к_₂Ь²~^Хпь- =

— f)ⁿo +2wi+…+2″^_1w^_₁ — fan

Алгоритм выполняет k- шагов, на каждом шагу выполняется 1 или 2 умножения. На каждом шагу требуется выполнить порядка 0(log²/w) двоичных операций. Алгоритм в целом выполняет порядка 0(ognog²m) двоичных операций.

• [1] Теорема 5.5 (китайская теорема об остатках). При попарно взаимно простых модулях тх,…, тг система сравнений {х = ах (тоАтх),…, х = «,.(modwr)}разрешима, и любые два решения сравнимы по модулю т = тЛ… тГ 4 Пусть х? и х// — два решения системы и х = х/ - х//. Тогда х = ()(modm,),
• [2] = 1, …, г, значит, х = 0(mod»?) в силу попарной взаимной простоты модулей. Найдем решение х системы. Пусть р, = т / mv тогда (хгт) = 1, значит, среди чисел 1,…, — 1 имеется такое целое пх, что рд = 1 (modra,), i = 1,…, г.
• [3] Тогда х = axi{nx + … + «;р, яг Все слагаемые суммы, за исключением /-го, делятся на тх, так как тх pyпри j Ф г, тогда х = «^"/(modm,) = «^mod/TZy), i = 1,…, г. ?
• [4] Посчитаем ср{пт) — количество целых чисел между 0 и пт — 1, не имеющих общих делителей с пт. Для каждого ненулевого числа j е Znm обозначим: jx е Zm и Д = j (modm), j2 е Zn и j2 = j (modn). Из теоремы 5.5 следует, чтокаждой паре соответствует единственное ненулевое число j е Znm, для которого выполнены оба сравнения: j =jx (modm), j =j2(modn). Заметим, что (j, пт) = 1 (j, п) = 1 и (/, т) = 1. Значит, множеству чисел j таких, что (j, пт) = 1, биективно соответствует множество пар чисел (j, j2) таких, что (jx, т) = 1 и (j2, п) = 1. Число возможных значений^ равноФ (т), дляу2 — равно ф (п). Отсюда ф (яш) = ф (я)ф (ш).? Следствие 2. Пусть п = pq, где pwq — простые. Тогда ф (я) можно вычислить по известным pwq за 0(log») двоичных операций, а числа/? и q можновычислить по известным п и ф (п) за 0(log5») двоичных операций. 4 Утверждение верно, если п четно, так как р = 2, q = п / 2, отсюдаф (я) — п / 2−1.