Свойства реляционной алгебры

Рассмотрим свойства операций реляционной алгебры [4].

I. Коммутативность:

Унарные операции:

• 1) ;
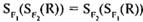• 2) 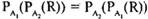, еслиА1= А2;
• 3) 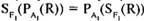, если Аttr (F1)А1;
• 4) 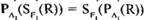, если Attr (F1)A1.

Бинарные операции:

• 5) JF (R, S) > JF (S, R);
• 6) U (R, S) > U (S, R);
• 7) CP (R, S) > CP (S, R).

II. Ассоциативность бинарных операций:

• 1) U (U (R, S), Т) > U (R, U (S, Т));
• 2) CP (CP (R, S), Т) > CP (R, CP (S, Т));
• 3)

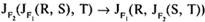
III. Идемпотентность унарных операций:

• 1) 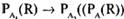, если, А = А1, А I А2;
• 2) 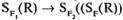, если F = F1 C F2.

IV. Дистрибутивность бинарных операций между бинарными:

• 1) SF (U (R, S)) > U (Sf®, Sf (S));
• 2) Sf (DF (R, S)) > DF (Sf®, SF (S));
• 3) Sf (CP (R, S)) > CP (Sf®, S), если Attr (F) I Attr (S);
• 4) Sf1 (Jf (R, S)) > Jf (Sf®, SF (S)), если Attr (F) I Attr (S);
• 5) Pa (U (R, S)) > U (Pa®, Pa (S));
• 6) Pa (CP (R, S)) > CP (Pa®, Pa (S)).

V. Факторизация унарных операций:

• 1) U (Sf®, Sf (S)) > Sf (U (R, S));
• 2) CP (Sfr®, Sfs (S)) > Sf (CP (R, S)), где F = FR C FS;
• 3) JF (SF®, SF (S)) > Sf (Jf (R, S)), где F = FR C FS;
• 4) DF (Sfr®, Sr (S)) > Sfr (DF (R, S)), где FR > FS;
• 5) U (Pa®, Pa (S)) > Pa (U (R, S));
• 6) CP (Par®, Pas (S)) > Pa (CP (R, S)), где A = AR u AS.

Реляционная алгебра в процедуре использования БД

Перечисленные правила используются прежде всего при формировании и оптимизации запросов.

Описание построения БД

Реляционная алгебра больше предназначена для описания процедур запросов (выборки) и обновления. Дело в том, что РА (равно как и РИ, как будет показано позднее) не затрагивают вопросы обеспечения целостности при создании и обновлении БД. Иными словами, они непригодны для того, чтобы СУБД могла автоматически проверить истинность или ложность следствий из заданных в схеме БД [9] ограничений целостности.

Потребовался аппарат с более простой интерпретацией и алгоритмической разрешимостью проблемы выводимости (или логических следствий) разумной комбинаторной сложности.

Это удалось сделать с помощью функционального подхода (формул однозначных {1:1, 1: М} F-зависимостей и многозначных {1:М и прежде всего — М: М} MV-зависимостей) и, как следствие, путем выполнения процедуры нормализации.

F-зависимости обеспечивают переход к первой (???), второй (2НФ), третьей (ЗНФ) нормальным формам представления данных. MV-зависимости позволяют строить четвертую (4НФ) и пятую (5НФ) нормальные формы.

Доказательства положений для Fи MV-зависимостей базируются на реляционной алгебре, в связи с чем их иногда относят к аппарату реляционной алгебры.

Функциональные (однозначные) F-зависимости

Функциональные зависимости являются обобщением понятия ключа: значения кортежа на одном множестве X атрибутов определяют значения на другом множестве Y атрибутов; X, Y I R; R — схема отношения R.

Пусть имеется r® и X, Y I R.

Отношение удовлетворяет функциональной зависимости (ФЗ) X > Y, если ?Y (?х_х ®) имеет не более одного кортежа для любого (V)x I X. Проверка проводится так (рис. 4.1): если кортежи t1(X) = t2(X), то должно удовлетворяться условие t1(Y) = t2(Y).

Такие однозначные зависимости называются F-зависимостями. Множество F-зависимостей также обозначается F. Иначе сказанное записывается в виде: F I X > Y влечет X > Y или говорят об аксиоме вывода.

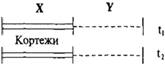
Рис. 4.1. F-зависимость.

Аксиома вывода (правило): если отношение удовлетворяет некоторым F-зависимостям, то оно должно удовлетворять и другим F-зависимостям.

Пример 4.1. Пусть имеем расписание занятий «Расписание» (День, Время, Аудитория, Преподаватель, Группа). Введем две ФЗ:

f1: День Время Аудитория > Преподаватель Группа,.

f2: День Время Преподаватель > Аудитория Группа.

Далее используем следующие ФЗ:

f1: Студент > Курсовая работа,.

f2: Студент > Преподаватель,.

f3: Преподаватель > Кафедра,.

f4: Кафедра > Факультет,.

f5: Студент > Факультет.

Пусть R = {a, …, А}; X, Y, Z, W I R. Для любого r® справедливы следующие аксиомы вывода.

F1. Рефлексивность: X = X. Проекция от селекции? X (?X=х ®) имеет не более одного кортежа. Например, Студент > Студент.

F2. Транзитивность: если X >? и? > ?, то X > ?. Если t1(X) = t2(X), то t1(Y) = t2(Y) по определению. Если t,(Y) = t2(Y), то и t,(Z) = t2(Z). Следовательно, если t1(X) = t2(X), то t1(Z) = t2(Z).

Иначе говоря, из Студент-4 Преподаватель и Преподаватель -4 Кафедра следует Студент > Кафедра.

F3. Пополнение: если X > Y, то XZ > Y.

Из X > Y следует (), что? Y (?x=x®) имеет не более одного кортежа для «x I X. Если Z I R, то? XZ=xz ® I? X=х ® и ?Y (?XZ=xz®) I ?Y (?X=x®) имеет не более одного кортежа.

Следовательно, если Студент > Преподаватель, то Студент Кафедра > Преподаватель.

Или из, А > В следует АС > В и AD > В, АВС > В, ABD > В, ACD > В, ABCD > В.

F4. Псевдотранзитивность: если X > Y, YZ > W, то XZ > W.

Если t1(X) = t2(X), то t1(Y) — t2(Y) по определению. Если t1(YZ) = t2 (YZ), то и t1(W) = t2(W). Следовательно, из t1(XZ) = t2(XZ) имеем t1(X) = t2(X) и t1(Z) = t2(Z), t1(Y) = t2(Y), t1(YZ) = t2(YZ) и t1(W) = t2(W). Иначе, если Студент > Преподаватель, Преподаватель Кафедра > Факультет, то Студент Кафедра > Факультет или из A > В, ВС > D следует АС > D.

F5. Аддитивность: если X > Y и X > Z, то X > YZ.

По определению pY (sx=x®) и pz (sx=z®) имеют не более одного кортежа. Если sYZ (sX=x®) имеет более одного кортежа, то хотя бы одна зависимость имеет более одного кортежа.

Следовательно, Студент > Преподаватель, Студент > Кафедра, то Студент Преподаватель > Кафедра или из, А > В, А > С следует, А > ВС.

F6. Проективность (в определенной степени обратна аддитивности): если X > ??, то X >? и X > ?.

По определению pyZ (?X=x®) и pz (?X=z®) имеют не более одного кортежа. Однако pY®)) = pY (?X=x®) и pY (?x=x®) тоже имеет более одного кортежа, т. e. X > Y.

Итак, Студент > Преподаватель Кафедра, то Студент > Преподаватель и Студент > Кафедра или если, А > ВС, то, А > С и, А > В.

Система F1-F6 является полной: с ее помощью можно получить (путем многократного применения) любую F-зависимость для множества F. Аксиомы F2, F5, F6 выводятся из F1, F3, F4. Покажем лишь два вывода.

Транзитивность F2 — частный случай аксиомы F4. Аксиома F5: если X > Y, X > Z, то из F1 следует YZ > YZ, из F4 следует XZ > YZ, из F4 следует X > YZ.

Аксиомы F1, F3, F4 иногда называют аксиомами Армстронга.

Замыканием множества F называется множество функций F+, содержащее все те зависимости, которые могут быть получены применением к F аксиом Армстронга.

Замыкание используется для определения биекции и ликвидации избыточности множества функциональных зависимостей, что можно сформулировать в виде леммы.

Лемма. Функциональная зависимость X > Y выводима из аксиом Армстронга, если Y с Х+.

Доказательство приводится в [4].

Вычисление F+ достаточно сложная процедура. Например, если F = (Аt > Вt, …, Аn > Вп), то F+ включает, А > Y, где Y — подмножества множеств {В1, …, Bn} и их количество составляет 2n.

Более того, если F-множество F-зависимостей над R и X I R, то в F+ существует зависимость X > Y такая, что подмножество Y максимально, т. e. Z I Y для любой другой F-зависимости X > Z в F+.

Если F = {А > D, АВ > DE, СЕ > G, Е > Н}, то можно показать, что (АВ)+= ABCDEH.

Для F = {АВ > С, АЕ > G, ВС > D, D > Е, В > AЕ, EG > К} (АВ)+ = ABCDEGK.

Сложность алгоритма во времени зависит от размера входного множества F-зависимостей. Следовательно, надо стремиться к минимизации F-множества. Это способствует согласованности и целостности БД (меньше проверок при модификации).

Действительно, множество F = {А > В, В > С, А > С, АВ > С, А > ВС} выводимо из множества G = {А > В, В > С}. Говорят, что множество G покрывает множество F (G эквивалентно F или G I F).

На пути минимизации возникает две проблемы: неизбыточность; устранение постороннего атрибута (редуцирование).

Множество F-зависимостей F называется неизбыточным, если нет F' с F такого, что F' º F. В неизбыточном множестве могут быть посторонние атрибуты, которые могут быть удалены (множество может быть редуцировано).

Пусть имеется множество F-зависимостей F = {Xi > Yi, i = 1, n}. Множество атрибутов Zi I? i называется посторонним в Xi, если (?i?i) >ji. может быть получено в замыкании F+i.

Множество F-зависимостей F называется каноническим, если любая F-зависимость из F имеет вид X > A, a F — редуцировано и неизбыточно.

Множество F-зависимостей F минимально, если оно содержит не более F-зависимостей, чем любое эквивалентное множество F-зависимостей.

Теория F-зависимостей используется при нормализации (1НФ — ЗНФ), однако, кроме F-зависимостей, могут существовать MV-зависимости. Для них используются несколько иные правила.