Решение задач устойчивости методом конечных элементов

Подробное изложение МКЭ к решению задач устойчивости можно найти в соответствующей литературе. Ниже приведены лишь необходимые матрицы из работы [15]. По-прежнему для решения задачи используются идеи метода перемещений, основная система которого состоит из двух типов стержней (см. рис. 4.8).

Рассмотрим задачи устойчивости систем, состоящих из прямолинейных стержней постоянного сечения. В существующих работах для решения задач устойчивости берут кубический полином, который обычно используется при решении задач прочности и колебаний. В настоящем учебнике для описания формы потери устойчивости одного элемента, у которого по концам нет шарниров, принимаем следующую функцию с четырьмя произвольными параметрами /":

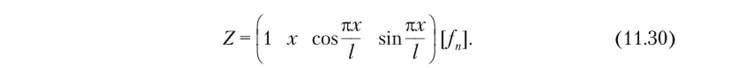
В отличие от кубического полинома эта функция более точно описывает форму потери устойчивости одного стержня и в ряде случаев дает точное значение критической нагрузки. При определении критической нагрузки необходимо знать угол поворота. С целью его определения вычислим производную от перемещения:

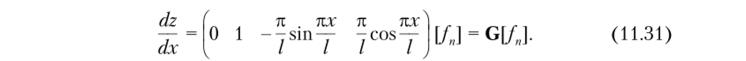
Для определения параметров /" нужно проделать ту же последовательность матричных операций, что и при выводе матрицы жесткости. При этом за положительные примем перемещения, вращающие стержень по ходу часовой стрелки. В итоге матрица будет иметь вид.

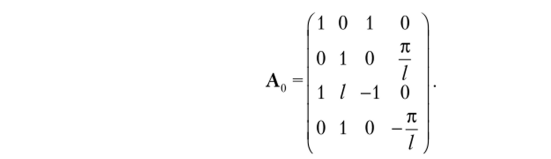
Вычислим матрицу, обратную по отношению к А₍₎ с учетом принятого правила знаков:

нужно задать напряженное состояние стержня. Примем, что он нагружен постоянной продольной силой. Тогда Подставляя матрицы (11.31), (11.32), (11.34) в выражение (11.33) и выполняя указанные операции, получаем матрицу потенциала нагрузки для прямолинейного стержня, нагруженного постоянной продольной силой:

Поскольку форма потери устойчивости определяется функцией (11.30), то следующую исходную матрицу — матрицу жесткости — составляют для той же функции, используя обычную процедуру МКЭ [91. Матрица, представляющая упругие свойства системы, С = El[ 1], а матрицу В получают путем двукратного дифференцирования функции (11.30):

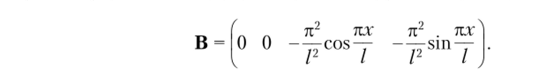
Выполняя указанные в выражении (4.17) операции, находим матрицу жесткости для этого случая:

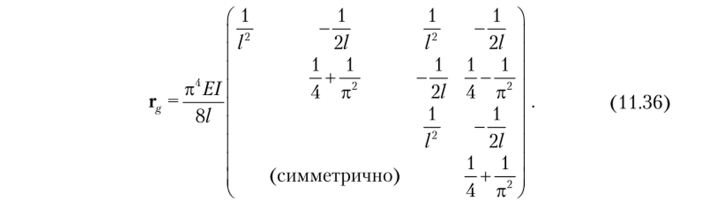
Если стержень, входящий в систему, не нагружен продольной силой, матрица потенциала нагрузки (11.35) будет нулевой. Для таких стержней в случае изгиба при потере устойчивости нужно использовать матрицу жесткости (4.17), так как она дает точное значение реакций при отсутствии продольной силы.

Как и при решении задач динамики, для стержня, у которого на одном конце шарнир, можно понизить порядок матрицы потенциала нагрузки и матрицы жесткости. Для описания формы потери устойчивости такого стержня принимают функцию с тремя произвольными параметрами с началом координат на защемленном конце:

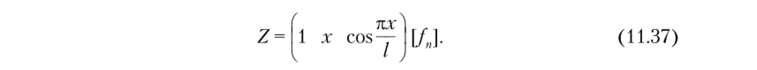
Эта функция обеспечивает более точный результат при решении задач устойчивости.

Повторяя вывод матрицы потенциала нагрузки и матрицы жесткости для функции (11.37), получаем.

Порядок обхода перемещений в матрицах следующий: Z, Z_;, Zj.

Если продольная сила отсутствует, то матрица Y., будет нулевой. В матри;

п²Е1 ., 3 EI

цу жесткости (11.39) такого стержня вместо войдет множитель —j~,

и она примет вид (4.19).

Покажем применение полученных матриц на примере расчета рамы (рис. 11.14, а) из работы [ 15]. Основная система изображена на рис. 11.14, б.

Сначала составим исходные матрицы. Матрица жесткости стержня BD представлена матрицей (11.36). Матрицы жесткости остачьных стержней определяются матрицей (4.17), т. е. для стержней, в которых отсутствует продольная сила, матрицы жесткости следует брать из параграфа 4.3.

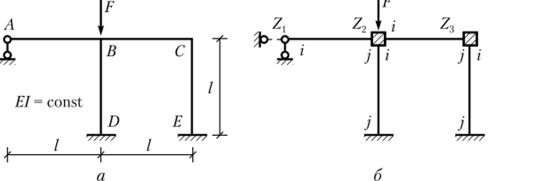
Рис. 11.14. Основная система метода перемещений.

Матрицу потенциала нагрузки (11.35) построим только для стержня BD, так как для остальных стержней эти матрицы нулевые. По схемам деформации (углы поворота задаем по часовой стрелке, а линейные смещения — влево) запишем матрицы:

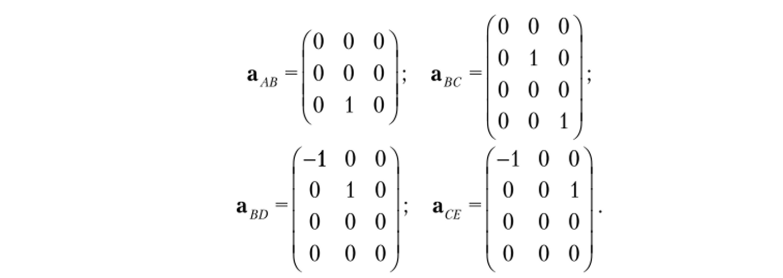
Далее следуют матричные операции.

1. Составление матрицы жесткости всей системы:

2. Составление матрицы потенциала нагрузки всей системы:

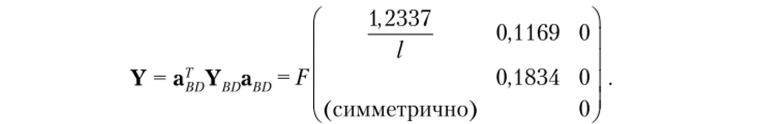
Приведенную выше методику целесообразно использовать для матриц высокого порядка, так как в таком случае F_min находят через А,_шах. В данном случае, как следует из матрицы Y, решение сводится к квадратному уравнению. Поэтому проще сразу составить определитель |К — Y| = 0. Раскрывая его, получим квадратное уравнение относительно F

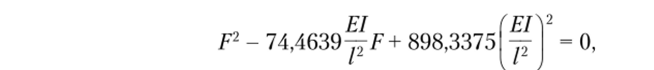
EI.

в результате решения которого имеем F_min = 15,14−7^-. Решение методом пе;

[ EI

ремещений с помощью трансцендентных функций дает F_min = 15,1-^-. Ре;

" ЕЛ

зультат, полученный с помощью кубического полинома, — F_min = 15,41.

Изложенный подход к решению задач устойчивости можно использовать, например, при переменном сечении стержня, при переменной по длине стержня нагрузке и т. д. Даже для стержней постоянного сечения изложенная процедура удобна тем, что она легче программируется с помощью стандартных программ матричных операций, нежели решение трансцендентных уравнений, получаемых при использовании табличной формы метода перемещений.

Например, при линейном изменении нагрузки по длине стержня, в основание которого помещено начало координат, матрица (11.34) примет вид.

(дЛ.

F= ql 1 — 11 ], где q — вес стержня на единицу длины. В стержне посто;

Ч ^)

янного сечения это выражение может имитировать нагрузку от действия его силы тяжести.

Получим матрицу потенциала нагрузки для стержня, защемленного внизу и имеющего шарнирное опирание на верхнем конце. Для описания формы потери устойчивости примем функцию (11.37). На основании выражения (11.33) запишем следующую матрицу:

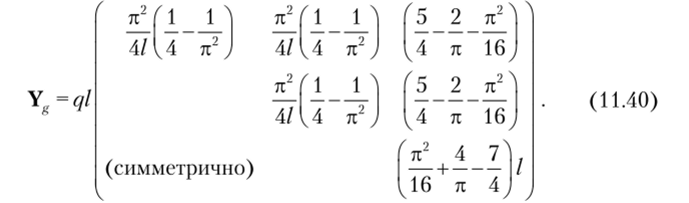
Матрица жесткости в этом случае определяется матрицей (11.39), также полученной с помощью функции (11.37).

Для оценки точности, которую обеспечивает приведенная матрица, определим критическую силу свободно стоящего защемленного внизу вертикального стержня постоянного сечения, нагруженного силой /'на свободном конце, с учетом его силы тяжести. Силы F и q связаны соотношением F = 2ql, где / — длина стержня. Задача решается с одним неизвестным (линейное перемещение вверху). Так как здесь два вида нагружения, то при решении используют матрицы потенциала нагрузки (11.38) и (11.40) и матрицу жесткости из параграфа 4.3, из первых элементов первых строк которых и составляется определитель:

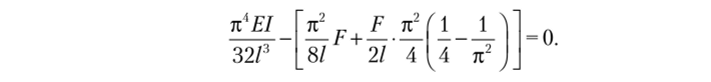
EI.

EI

Отсюда F_mjn = 2,148-уу. Этот результат на 2,9% меньше результата, приведенного в работе [26], но получен он более коротким путем.

Аналогично решают и другие задачи, которые не охватываются табличной формой метода перемещений. Приведенные матрицы можно использовать и при расчете рам по деформированной схеме.

При реализации изложенного подхода следует помнить, что он дает точные результаты при общепринятом числе основных неизвестных метода перемещений только для свободных рам [ 131. В случае расчета несвободных рам, т. е. рам, в которых отсутствуют линейные смещения узлов, для получения более точного результата необходимо делить сжатые стержни по крайней мере на два элемента.

Для удобства использования приведенных выше матриц в них подставлено численное значение п с точностью до шестого знака после запятой:

Для стержня, изображенного на рис. 4.8, б, с началом координат на за;

кх

щемленном конце принята функция Z = /, + f.pc + /₃cos —. Тогда имеем.

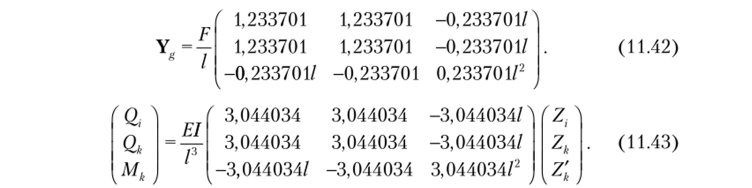
Матрица жесткости всей конструкции по-прежнему составляется по формуле (4.19). Матрица потенциала нагрузки составляется аналогичным образом, т. е.

Уравнение устойчивости имеет вид.

При расчете несложных рам элементы определителя (11.45) можно определять по таблице типа табл. 10.1. Такая таблица составлена ниже (табл. 11.2). Ординаты для нее взяты из матриц (11.41)—(11.43). При вычислении реакций в дополнительных связях можно пользоваться общепринятым правилом знаков. Ради наглядности элементы определителя представлены эпюрами моментов.

МКЭ позволяет легко получить решение и при действии распределенной вдоль оси стержня продольной нагрузки (например, собственного веса). В этом случае при начале координат внизу.

Задаваясь соотношением между сосредоточенной силой и распределенной нагрузкой, можно определить критический параметр для всей системы.

Таблица 11.2

Реакции с учетом продольных сил от единичных перемещений.

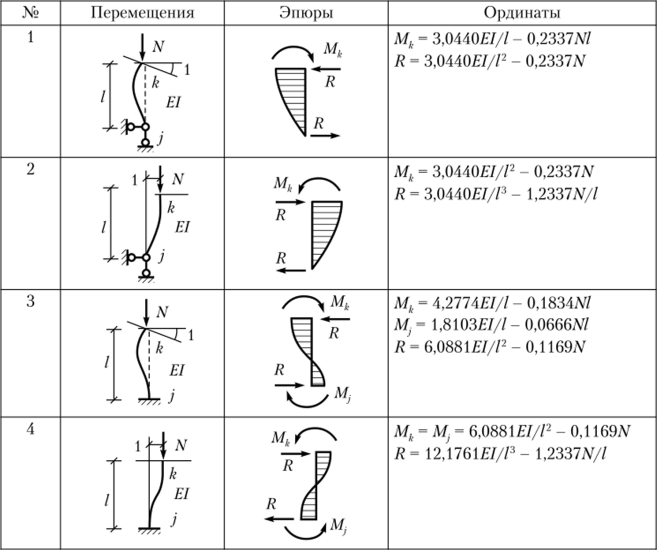
При одновременном действии обоих типов нагрузки ее потенциал представляется суммой двух матриц Y = Y_;) + Y. Для приведенных выше функций перемещений матрицы потенциала распределенной нагрузки имеют вид.

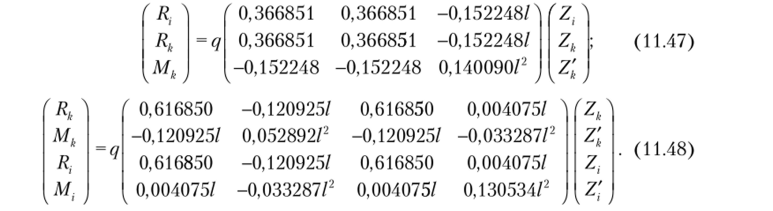
Матрицы жесткости остаются прежними — (11.43), (11.41). Эти матрицы также можно свести в таблицу типа табл. 11.2. При расчете рам для стержней, в которых отсутствуют продольные силы, берутся обычные матрицы жесткости, представленные формулами (10.14) и (10.16).

При решении задач в матричной форме удобно свести задачу устойчивости к проблеме собственных значений, чтобы воспользоваться стандартными программами матричных операций. С этой целью из матрицы Y выносится параметр F, что возможно на основании четвертого допущения (см. параграф У.2): |К — FY₀| = 0. Затем это выражение делится на F, умножает;

ся слева на К ', и в него вводится обозначение X = —. В результате после перемены знаков получаем Для оценки точности результатов, даваемых МКЭ, рассмотрим сначала два примера из гл. 10.

Пример 11.8. Определим F_K|) для рамы из примера 10.1 (см. рис. 10.5). Решение

Решим задачу с одним неизвестным — углом поворота. Для горизонтальных стержней понадобится только один элемент из матрицы жесткости (4.16) — г₃₃ = EI

= 3 —. Для вертикального стержня также берется только один элемент из мат;

FZ.

рицы (10.12) — г_м= 4,277 733 —, а из матрицы потенциала нагрузки (11.36) —.

^h 2

элемент y_i = 0,183 425Fh. В г_:а заменим / через А: / = -А.

Составим уравнение устойчивости (11.16):

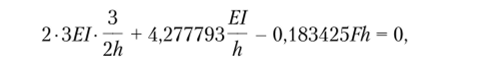
Е1.

отсюда F = 72,39—, a v = 8,51. Расхождение с точным значением — 49%.

КР _h2

Этот результат показывает, что применение МКЭ к несвободным рамам только с неизвестными углами поворота приводит к неприемлемым результатам. Нужно по крайней мерс ввести еще один узел посередине сжатого стержня, чтобы в описании формы потери устойчивости присутствовало линейное смещение (рис. 11.15, а).

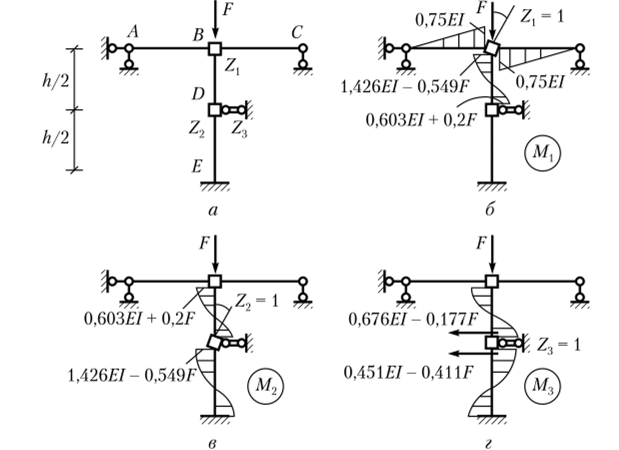
Рис. 11.15. Эпюры моментов от единичных перемещений Составим матрицу жесткости всей рамы по табл. 11.2. Эпюры моментов от единичных перемещений изображены на рис. 11.15, б—г. Реакции в связях определим обычным способом, путем вырезания отдельных частей рамы и составления уравнений равновесия. Таким же образом с помощью матрицы (11.11) составим матрицу потенциала нагрузки для всей рамы:

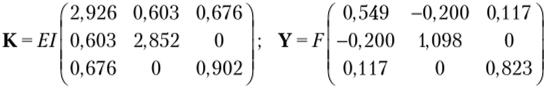
Вычисления выполняем с помощью системы MATLAB (операции В = inv (K); L = BY₀; [v, cl | = eig (L); F = inv (d)).

В результате вычислений получаем, что F_K]) = 0,9078?7 = 181,56 кН. Определим критический параметр:

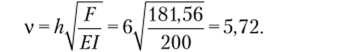
Расхождение с точным значением составляет приблизительно 0,1%.

Пример 11.9. Определим F для рамы из примера 10.3 (см. рис. 10.7, а).

Решение

Основная система метода перемещений показана на рис. 10.7, б. Составим исходные матрицы. Для стержня ВС берется матрица жесткости (11.41), для стержней АВ и DE — матрица жесткости (11.43), а для стержня ВО — матрица из формулы (4.17):

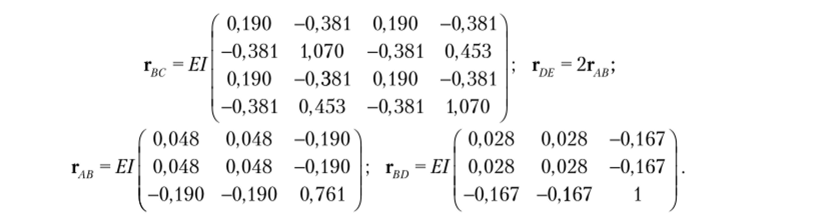
Составим матрицы потенциала нагрузки. Для стержня ВС берется матрица (11.11), для стержней АВ и DE — матрица (11.42):

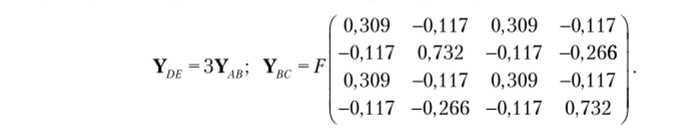
Составим матрицы преобразования перемещений:

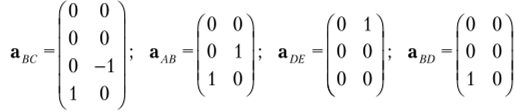
Начало и конец каждого стержня показаны на рис. 11.14, б. Дальнейший расчет выполним на ЭВМ:

В результате получим F_K]y = 0,2042;250 = 51,05 кН. v = 4⁰, 2042 =1,81. Расхождение с точным значением критического параметра составляет 1,17%. Поскольку в МКЭ реализован энергетический критерий устойчивости, то, как и следовало ожидать, при правильном его использовании значения критических параметров получаются больше истинных или равны им.

В следующих примерах рассмотрим более сложные случаи. В одном примере определим критическую силу для стойки ступенчатого сечения, а в другом — от нагрузки, распределенной по длине стержня.

Пример 11.10. Определим критическую силу для стержня со ступенчатым изменением жесткости (рис. 11.16, а). В данном случае имеем два неизвестных перемещения.

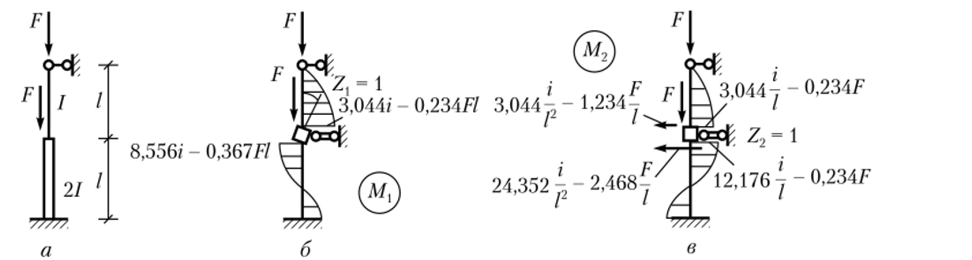
Рис. 11.16. Эпюры моментов и потенциала нагрузки от единичных перемещений.

Решение

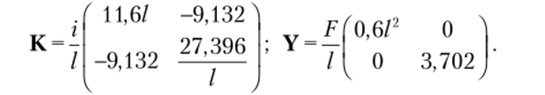
EI.

Введем обозначение i = —. Так как система очень простая, то матрицы жесткости и потенциала нагрузки составим, но табл. 11.2 (рис. 11.16, б, в):

ЕЛ ,;

Получаем F = 4,8144—, v = >/4,8144 =2,19. Расхождение с точным значением параметра составляет 0,92%.

Пример 11.11. Определим критическую нагрузку на раму, представленную.

Е1

на рис. 11.17, а, учитывая равенства i——; F =.

Решение

По табл. 11.2 и 10.1 построим эпюры моментов от единичных перемещений (рис. 11.17, б—г). По этим эпюрам составляется матрица жесткости всей рамы:

В рассматриваемом случае имеются два типа нагрузки, поэтому составим две матрицы потенциала нагрузки. Для составления матрицы Y_p можно воспользо;

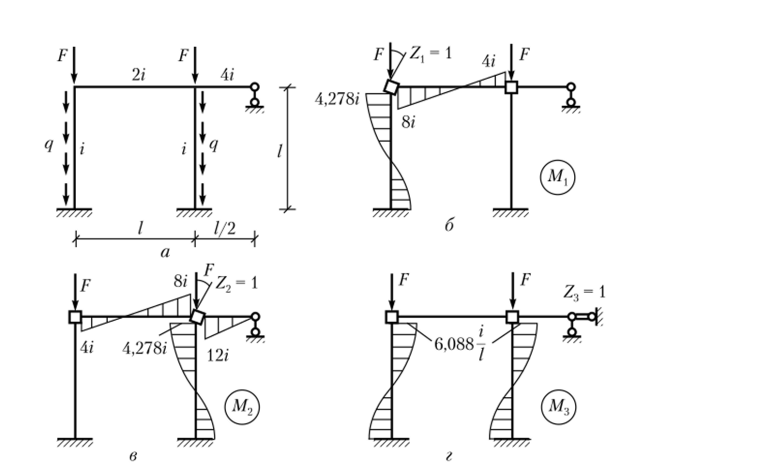
Рис. 11.17. Рама, нагруженная сосредоточенной и распределенной нагрузкой.

ваться табл. 11.2. Потенциал распределенной нагрузки составим по матрице (11.40):

Составим уравнение устойчивости:

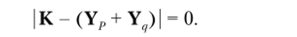
Для вычисления критической нагрузки используем программу из примера 11.7: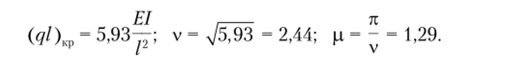

EI

Если не учитывать сосредоточенные силы, то (ql)_1ф = 18,44—, и наоборот, если не учитывать распределенную нагрузку, а оставить только сосредоточенную, EI

то F_K|> = 8,78—. Совершенно очевидно, что учет распределенной нагрузки понижает значение критической силы.

Упражнение 11.4. Определите критический параметр сжатой стойки рамы, представленной на рис. 11.18, а.

Упражнение 11.5. Определите критическую нагрузку для стойки, изображенной па рис. 11.18, 6, энергетическим методом и проверьте точность решения методом перемещения.

В заключение этого параграфа отметим, что при построении таблиц типа 11.2 для распределенной нагрузки нужно помнить о переменности продольной силы по высоте стержня. Если деформированная ось стержня несимметрична относительно его середины, что имеет место для стержня с шарниром на одном конце, то элементы таблицы будут различными для каждого конца стержня.

Таблицы типа 11.2 могут оказаться полезными при программировании, так как они не содержат специальных функций, что, естественно, упрощает программирование. Удобно их использовать и при расчете рам по деформированной схеме (см. параграф 10.6).