Отношение достижимости модулей графов

Пусть G = (X, Г) — граф модульной структуры, х_г, х-. — вершины, принадлежащие X. Если в графе G существует ориентированная цепь от х, к Хр то вершина х, — — достижима из вершины х,-. Справедливо следующее утверждение: если вершина Xj достижима из х, ах₍— из Хр то X/ достижима из х^ Доказательство этого факта очевидно. Рассмотрим бинарное отношение на множестве X, которое определяет достижимость между вершинами графа. Введем обозначение х, —> х, для достижимости вершины х, — из Xj. Отношение транзитивно. Обозначим через Я (х,) множество вершин графа G, достижимых из х_;. Тогда равенство.

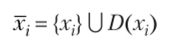
определяет транзитивное замыкание х, по отношению к достижимости.

Докажем следующую теорему.

Теорема 1.1. Для выбранного компонента связности графа модульной структуры любая вершина достижима из корневой, соответствующей данному компоненту, т. е. выполняется равенство (х/— корневая вершина).

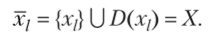
Доказательство. Предположим, вершинах, (х, е X) недостижима из Xj. Тогда х, ё X/ и множество X' = X х), непусто. Поскольку выбранный компонент графа связанный, то существуют вершина х, — е х, и цепь /7(х_;, xj), ведущая от х, к х,-. Исходя из ацикличности графа G, в X' должна существовать простая цепь Н (х/, xj), где в вершину x_f не входят дуги (данная цепь может быть пустой, если X' состоит только из х,). Рассмотрим цепь Я (х/, xj) = Н (х/, х,) U Я (х, xj). Это означает, что модуль х. достижим из вершин х, и Xj и обе вершины не содержат входящих дуг. А это противоречит определению графа модульной структуры с единственной корневой вершиной. Теорема доказана.

Основное требование для обеспечение достижимости — это отсутствие неориентированных циклов в графе. Исходя из графа на рис. 1.4, отмечаем, что граф содержит ориентированный цикл и модули, соответствующие вершинам х₄, х₅, ж₆, никогда выполняться не будут. Таким образом, результаты теоремы 1.1 усиливают требование отсутствия ориентированных циклов в графе модулей.

Для анализа матричного представления отношения достижимости графа модульной структуры рассмотрим граф матрицы достижимости, приведенной на рис. 1.1.

Коэффициент а, у= 1, если модуль, соответствующий индексу /, достижим из модуля, соответствующего индексу i. Следующие результаты основаны на известной теореме из теории графов.

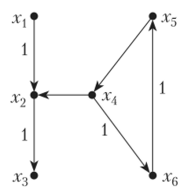
Рис. 1.4. Граф с ориентированным циклом.

Теорема 1.2. Коэффициент ту l-й степени матрицы смежности Доопределяет количество различных маршрутов, содержащих / дуг и связывающих вершину X/ с вершиной^{-ориентированного} графа.

Рассмотрим следующие три следствия из этой теоремы^[1].

_ П

Следствие 1.1. Матрица М = '?_JM^t, где М — матрица смежности ориен;

i=i

тированного графа с п вершинами, совпадает с точностью до числовых значений коэффициентов с матрицей достижимости А.

Доказательство. В ориентированном графе, содержащем п вершин, максимальная длина пути без повторяющихся дуг не может превышать п. Поэтому последовательность степеней матрицы смежности М¹, где i = 1,2,.

я, определяет количество всех возможных путей в графе с количеством дуг < п. Пусть коэффициент т_1} матрицы М отличен от нуля. Это означает, что существует степень матрицы М>, у которой соответствующий коэффициент т_{} также отличен от нуля. Следовательно, существует путь, идущий от вершины Xj к Хр т. е. вершина ^ достижима из х_г Данное следствие определяет связь матрицы вызовов графа модульной структуры, совпадающей с матрицей смежности А/, с матрицей достижимости А и определяет алгоритм построения последней.

Следствие 1.2. Пусть для некоторого i в последовательности степеней матрицы смежности М* существует коэффициент т_Х1 > 0. Тогда в исходном графе существует ориентированный цикл.

Доказательство. Пусть m_(i > 0 для некоторого I. Следовательно, Xj достижима из x_v т. е. существует цикл. Согласно теореме 1.2 данный цикл имеет / дуг (в общем случае повторяющихся).

Следствие 1.3. Пусть п-я степень матрицы смежности М^п ациклического графа совпадает с нулевой матрицей (все коэффициенты равны нулю).

Доказательство. Если граф ациклический, то в нем максимально простой путь не может иметь больше чем п — 1 дуг. Если в М^п имеется коэффициент, отличный от нуля, то должен существовать путь, состоящий из п дуг. А этим путем может быть только ориентированный цикл. Следовательно, все коэффициенты М^п для ациклического графа равны нулю. Данное следствие предоставляет необходимое и достаточное условие отсутствия циклов в графе модульной структуры.

Для ациклических графов отношение достижимости эквивалентно частичному строгому порядку. Транзитивность отношения достижимости рассмотрена выше. Антисимметричность следует из отсутствия ориентированных циклов: если вершина х_} достижима из x_v то обратное неверно. Введем обозначение х_х > Хр если вершина Xj достижима из вершины x_v

Пусть G = (X, Г) — ациклический граф, соответствующий некоторой модульной структуре. Рассмотрим убывающую цепь элементов частично упорядоченного множества X:

где через знак «>» обозначено отношение достижимости. Поскольку X конечно, то цепь обрывается х_п > x_i2 > … > x_in. Вершина x_jn не имеет исходящих дуг, т. е. элемент x_in минимальный (ему соответствует модуль, который не содержит обращения к другим модулям). Максимальный элемент во множестве X — корневая вершина.

• [1] Доказательство этой теоремы приводится в работе (книга): Лаврищева Е. М., Грищенко В. Н. Сборочное программирование. Киев: Наукова думка, 1991. 287 с.