Оценка вычислительной сложности алгоритма

Подсчет вычислительной сложности алгоритма состоит из двух основных шагов:

Шаг 1. Выбор значимой операции или группы операций.

Шаг 2. Определение, какие из выбранных операций содержатся в теле алгоритма, а какие составляют накладные расходы или уходят на регистрацию и учет данных.

В качестве значимых часто (но не обязательно) выступают операции двух типов:

• · сравнение,
• · арифметические операции.

Арифметические операции разбиваются на две группы:

• · аддитивные,
• · мультипликативные.

Аддитивные операторы (сложения) включают сложение, вычитание, увеличение и уменьшение счетчика.

Мультипликативные операторы (умножения) включают умножение, деление, взятие остатка по модулю.

Разбиение на эти две группы связано с тем, что умножения работают дольше, чем сложения. На практике некоторые алгоритмы считаются предпочтительнее других, если в них меньше умножений, даже если число сложений при этом пропорционально возрастает.

Поскольку при анализе алгоритма выбор входных данных может существенно повлиять на его выполнение, желательно найти такие данные, которые обеспечивают как самое быстрое, так и самое медленное выполнение алгоритма, а также оценить среднюю эффективность алгоритма на всех возможных наборах данных. Очень часто при анализе алгоритма оценивается лишь наихудший (самый медленный) вариант.

Скорость роста алгоритма. Точное значение количества операций, выполненных алгоритмом, не играет существенной роли в его анализе, т.к. не является качественным показателем эффективности алгоритма. Более важной оказывается скорость роста этого числа при возрастании объема входных данных. Она называется скоростью роста алгоритма. Именно эта характеристика часто и фигурирует как оценка вычислительной сложности алгоритма.

Существенным является общий характер поведения алгоритмов, а не подробности этого поведения. Предположим, что количество операций четырех различных алгоритмов определяется в соответствии с функциями:

.

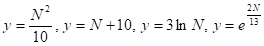
где — длина массива входных данных.

Если рассмотреть графики этих функций (рис. 1).

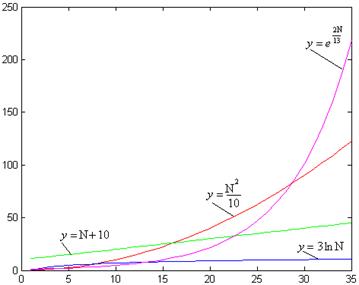
Рис. 1.

Например, на промежутке от 1 до 35, то становится очевидным, что несмотря на то, что функция:

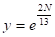
сначала растет медленнее всех рассматриваемых функций, при росте аргумента она увеличивает скорость возрастания быстрее всех остальных, что приводит к тому, что, начиная с некоторого значения аргумента, ее значения (а значит количество операций и время выполнения соответствующего алгоритма) становятся значительно больше значений всех остальных рассматриваемых функций.

Таким образом, при анализе алгоритмов существенным является поведении функции зависимости количества операций от размера входных данных при больших значениях аргумента.

Некоторые часто встречающиеся функции приведены в таблице 1. Очевидно, что при небольших размерах входных данных значения функций отличаются незначительно, при росте этих размеров разница существенно возрастает. Поэтому существенным является поведение функции на больших объемах входных данных, поскольку на малых объемах принципиальная разница оказывается скрытой.

Таблица 1.

Для иллюстрации последующего вывода рассмотрим пример функции, которая трактуется как закон зависимости количества арифметических операций некоторого гипотетического алгоритма от размера входных данных :

.

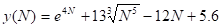
Предложенная функция является суммой нескольких функций, скорость возрастания которых различна. Очевидно, что скорость роста всей будет определяться самым быстровозрастающим слагаемым —. Иначе говоря, быстрорастущие функции доминируют функции с более медленным ростом, что приводит к тому, что если сложность алгоритма представляет собой сумму двух или нескольких функций, то для оценки алгоритма целесообразно отбрасывать все функции, кроме тех, которые растут быстрее всех.

Определение. Говорят, что функции и связаны соотношением (или сравнимы):

(читается: функция есть О-большое от), если.

.

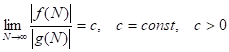
Рассмотрим другой пример:

.

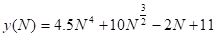
Ясно, что скорость возрастания будет определяться первым слагаемым —, остальными слагаемыми при оценке скорости роста можно пренебречь. Кроме того:

.

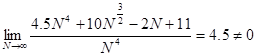
Из чего вытекает, что.

.

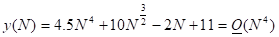
Отбрасывая все младшие члены, скорость роста которых меньше, получаем порядок вычислительной сложности алгоритма. В предыдущем рассмотренном примере поскольку, то соответствующий гипотетический алгоритм имеет вычислительную сложность порядка .