Численное решение систем линейных уравнений

Классы задач линейной алгебры При численном решении большого круга задач в конечном итоге происходит их линеаризация, в связи с чем в соответствующих алгоритмах весьма широко используются методы линейной алгебры. В их числе:

решение систем линейных алгебраических уравнений (СЛАУ);

вычисление определителей матриц ;

нахождение обратных матриц ;

определение собственных значений и собственных векторов матриц ;

Постановка задачи решения СЛАУ:

(1).

где — квадратная матрица коэффициентов размерности n, — вектор неизвестных, — вектор свободных коэффициентов. Иногда СЛАУ представляют в виде расширенной матрицы размерности n Ч n+1, где в качестве последнего столбца фигурирует вектор свободных коэффициентов. В координатном представлении такая СЛАУ выглядит следующим образом:

. (2).

Для решения СЛАУ применяют в основном два класса методов: прямые (выполняемые за заранее известное количество действий) и итерационные (обеспечивающие постепенную сходимость к корню уравнения, зависящую от многих факторов). Прямые методы обычно применяются для решения систем порядка n < 200, для бульших n используются итерационные методы. Перед решением СЛАУ требуется проанализировать корректную постановку задачи:

Если — решение существует и единственно. Если же определитель равен нулю, то тогда, если матрица вырождена (т.е. ее можно преобразовать к виду, когда как минимум одна строка коэффициентов — нули) решений бесконечное множество, иначе решения не существует.

Если не имеет элементов с большими по модулю значениями — решение устойчиво (см. пример к главе 1). Показателем плохо обусловленных систем является .

Алгоритм метода Гаусса Прямой ход.

Идея метода состоит в последовательном исключении неизвестных из системы n линейных уравнений. На примере первого уравнения системы (2) рассмотрим выражение для x1:

.

Подставим выражение для x1 во второе и все остальные уравнения системы:

Для расширенной матрицы коэффициентов это означает, что каждый элемент первой строки следует поделить на диагональный элемент, а все остальные строки преобразовать, как показано выше. Таким образом, станут равны нулю все коэффициенты первого столбца, лежащие ниже главной диагонали. Затем аналогичная процедура проводится со второй строкой матрицы и нижележащими строками, при этом первая строка и первый столбец уже не изменяются. И так далее до тех пор, пока все коэффициенты, лежащие ниже главной диагонали, не будут равны нулю.

Общие формулы прямого хода:

(3).

k = 1… n, j = 1… n+1. Звездочкой отмечены элементы k-й строки с измененными значениями, которые будут подставлены в следующую формулу. Для определенности будем считать первый индекс — по строкам, второй — по столбцам.

(4).

i = k +1…n, j = 1… n+1, k фиксировано в уравнении (3). Для уменьшения количества действий достаточно изменять значения элементов, находящихся выше главной диагонали.

Обратный ход Второй этап решения СЛАУ методом Гаусса называется обратным ходом и состоит в последовательном определении xk, начиная с xn, так как для последнего решение фактически получено. Общая формула:

. (5).

Таким образом, вычисление корней происходит за 2/3 n3 арифметических действий.

Выбор главного элемента.

Для уменьшения погрешности вычислений следует стремиться к тому, чтобы на главной диагонали матрицы стояли максимальные по модулю значения коэффициентов. Алгоритмически этого можно добиться, переставляя строки таким образом, чтобы на диагонали стоял наибольший по модулю элемент текущего столбца. Такая процедура называется выбором главного элемента и осуществляется всякий раз при переходе к новой строке в прямом цикле метода Гаусса.

Погрешность метода. Расчет невязок.

Точность результатов будет определяться только точностью выполнения арифметических операций при преобразовании элементов матрицы, т. е. ошибкой округления. Контроль правильности полученного решения осуществляется подстановкой полученных значений x1… xn в исходную систему уравнений и вычислением невязок, т. е. разностей между правыми и левыми частями уравнений:

где k = 1… n. (6).

Специально отметим, что подставлять найденные значения следует в исходную (не преобразованную к верхнетреугольному виду) систему.

Преимущества и недостатки метода.

Преимущество метода в том, что он позволяет достичь результата за заранее известное и фиксированное число действий. Точность результатов будет определяться правильным выбором порядка коэффициентов в матрице и ее размерностью. Недостатком метода является резкое увеличение времени и погрешности вычислений с ростом n.

Блок-схема алгоритма метода Гаусса без выбора главного элемента.

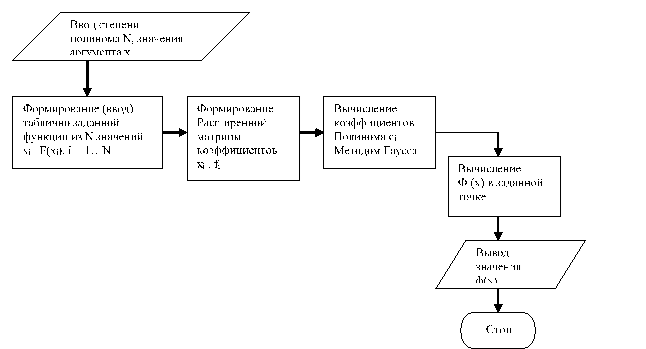
Итерационные методы решения систем линейных уравнений Простейшим итерационным методом решения СЛАУ является метод простой итерации. При этом система уравнений (1) преобразуется к виду (2), а ее решение находится как предел последовательности (3), где {n} - номер итерации. Утверждается, что всякая система (2), эквивалентная (1), записывается в виде .

Теорема о достаточном условии сходимости метода простой итерации утверждает, что если норма матрицы (), то система уравнений (2) имеет единственное решение и итерационный процесс (3) сходится к решению со скоростью геометрической прогрессии.

Теорема о необходимом и достаточном условии сходимости метода простой итерации: Пусть система (2) имеет единственное решение. Итерационный процесс (3) сходится к решению системы (2) при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы по модулю меньше 1.

На практике для обеспечения сходимости итерационных методов необходимо, чтобы значения диагональных элементов матрицы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами.

Представим СЛАУ в следующей форме, удовлетворяющей (3):

(4).

Зададим начальные приближения и вычислим правую часть (4), получим новые приближения, которые опять подставим в систему (4). Таким образом организуется итерационный процесс, который обрывается по условию, где — заданная погрешность.

К ускорению сходимости приводит использование приближения к решениям путем последовательного уточнения компонентов, причем k-я неизвестная находится из k-го уравнения. Такая модификация итерационного метода носит название метода Зейделя:

Критерий сходимости метода Зейделя: Пусть — вещественная симметричная положительно определенная матрица. Тогда метод Зейделя сходится.

Достоинствами метода простых итераций является простота программной реализации и более быстрый, по сравнению с линейными методами, поиск решения в матрицах большого размера. Недостатками являются сложный контроль условий сходимости и выбора начального приближения.

8)Интерполирование функций.

1) Необходимость: приблизить f (x) более простой функцией ф (х), совпадающей в узлах xi с f (xi), если f (x) определена только в узловых точках (результат эксперимента) или очень сложно вычисляется.

Условия Лагранжа: ф (х, с0, с1… сn) = fi,.

0 <_i < n, где сi — свободные параметры, определяемые из данной системы уравнений.

С помощью интерполяции решают широкий круг задач численного анализа: дифференцирование и интегрирование функций, нахождение нулей и экстремумов, решение дифференцированных и т. д. Термин интерполяция употребляют, если х заключено между узлами, если он выходит за крайний узел, говорят об экстраполяции (при которой трудно гарантировать надежность.

приближения).

2) Пусть ф (х) = с0 + с1х + с2×2 +…+ сnxn (канонический вид полинома) ;сетка узлов может быть неравномерной.

Коэффициенты сi определяются из условий Лагранжа:

Получившаяся СЛАУ относительно свободных.

параметров сi имеет решение, если среди узлов.

хi нет совпадающих. Ее определитель — определитель Вандермонда:

Общая блок-схема:

3) Пусть задано n+1 значение функции f (x) в узлах xj.

ф (х) = Pn (х) = i (x-xj)/(xi-xj) — полином Лагранжа.

Преимущества: потребуется решать СЛАУ для определения значения полинома в точке х.

Недостатки: для каждого х полином требуется читать заново.

Погрешность формулы: (*).

Увеличение числа узлов и, соответственно, степени полинома Pn (x) ведет к увеличению погрешности из-за роста производных .

4) ф (х) = Pn (x) = A0+A1(x-x0)+A2(x-x0)(x-x1)+…+An (x-x0)(x-x1)…(x-xn-1) — многочлен Ньютона для n+1 узла.

Коэффициенты Ф представляют собой разделенные разности и записываются в виде:

А0 = f0.

A1 = (f0-f1)/(x0-x1) = f01.

A2 = (f01-f02)/(x1-x2) = f012, где f02 = (f0-f2)/(x0-x2).

A3 = (f012-f013)/(x2-x3) = f0123, где f013 = (f01-f03)/(x1-x3), а f03 = (f0-f3)/(x0-x3).

и в общем случае Ak = (f01…k-1-f01…k)/(xk-1-xk).

Т.е. многочлен n-й степени выражается при помощи разделенных разностей через свои значения в узлах.

Преимущества: не решается СЛАУ, однако вычисление коэффициентов полинома не зависит от значения х и может быть вычислено только один раз. При добавлении нового узла также не происходит пересчета коэффициентов, кроме последнего.

После определения коэффициентов полинома Ньютона вычисление его значений при конкретных аргументах х наиболее экономично проводить по схеме Горнера:

P2(x) = A0+ (x-x0)(A1+(x-x2)(A3+…)…).

Погрешность определяется тем же соотношением (*).

Входящая в состав погрешности величина.

(х-хi) = wn (x) ведет себя при постоянном шаге так, как показано на рисунке. Многочлен Ньютона имеет погрешность 0(hn+1) и обеспечивает n+1-й порядок точности интерполяции.

! Между разделенными разностями и производными соответствующих порядков существует соотношение f (x) ~ n! F01… n, где n — степень производной. Это используется в численном дифференцировании и при оценке погрешностей интерполяции.

!Можно строить полиномы, не только проходящие через заданные точки, но и имеющие в них заданные касательные (интерполяционный многочлен Эрмита) или заданную кривизну. Количество всех полагаемых условий должно быть n-1, если n — степень полинома.

Основной недостаток интерполирования с помощью многочленов — неустранимые колебания, которые претерпевает кривая в промежутках между узлами.

При этом повышение степени интерполяционного полинома для большинства решаемых уравнений приводит не к уменьшению, а к увеличению погрешности.

Интерполяция сплайнами Происхождение термина «сплайны» связано с гибкой чертежной линейкой, которой пользовались для рисования гладких кривых, проходящих через заданные точки. Из теории упругости следует, что получающаяся кривая имеет постоянную кривизну и разрывы возникают лишь в третьей производной.

Обычно для сплайна выбирают кубический полином, определенный на интервале х из [xi-1, хi].

При этом вся кривая представляет собой набор таких кубических полиномов, с определенным образом подобранными коэффициентами аi, bi, ci, di, iпараметр сплайна.

!Если вдоль сплайна совершается механическое движение, то непрерывность второй производной предполагает непрерывность ускорения и, следовательно, отсутствие резких изменений приложенной силы.

N+1 узлов.

N интервалов.

4N неизвестных.

Условия подбора коэффициентов:

1)условия Лагранжа:

.

2)непрерывность первой и второй производной в узлах.

фi'(xi) = фi+1'(xi); фi"(xi) = фi+1(xi).

3) условия в крайних узлах x0 и xn. Обычно задают условия свободных концов сплайна:

ф1"(x0) = 0, фn"(xn) = 0.

Из полученных условий определяются зависимости между коэффициентами сплайнов:

В узле х = хi-1 коэффициент ai = fi-1.

В следующем узле x = xi выполняется условие ai+bihi+cihi2+dihi3 = fi, где элементарный шаг hi = xi — xi-1.

Потребуем непрерывности первой и второй производной на конце интервала фi/(x) = bi+2ci (x-xi-1)+3di (x-xi-1)2 ,.

фi//(x) = 2ci+6di (x-xi-1);

В узле x = xi первая производная фi/(xi) = bi+2cihi+3dihi2 (1).

фi+1//(xi) = bi+1 (2).

Приравнивая (1) и (2), получаем bi +2cihi+3dihi2 = bi+1.

Вторая производная фi//(xi) = 2ci+6cihi (3).

фi+1//(xi) = 2ci (4).

Приравнивая (3) и (4), получаем в свою очередь ci+3dihi = ci+1. Таким образом стыкуем все полиномы в узлах 1? i? n-1. В крайних точках диапазона ф1//(x0) = 2c1 = 0 > c1 = 0.

ф1//(xn) = 2cn+6dnhn = 0 > cn +3dnhn = 0.

Для всех 0? i? n вышеприведенные соотношения представляют собой полную систему 4n линейных алгебраических уравнений относительно коэффициентов сплайнов, которую можно привести к системе ЛАУ, выразив коэффициенты ai, bi, di через ci и решить методом Гаусса или прогонки.

Система N линейных уравнений для коэффициентов сi:

для ,.

где hi = xi-xi-1.

После определения коэффициентов ci, 2N коэффициентов bi и di вычисляются по формулам:

.

И N уравнений для ,.

Сплайновая интерполяция хороша тем, что требует знания в узлах только значений функции, но не ее производных.

Многомерная интерполяция.

1) Последовательная интерполяция на прямоугольной сетке. Пусть заданы z i j = z (xi, yj) требуется найти z (x, y). Сначала при фиксированных yj0 найдем значение z (x, yj0),.

Затем по полученному набору значений найдем z (x, y).

В случае интерполяции полиномом Лагранжа общая формула имеет вид.

где k и m — количество узлов по сторонам прямоугольной сетки.

2) Треугольная конфигурация узлов.

z (x0, x1, y) = [z (x0, y)-z (x1, y)]/(x0-x1).

z (x, y0, y1) = [z (x, y0)-z (x, y1)]/(y0-y1).

Многочлен Лагранжева типа в этом случае имеет вид.